Complete Solutions to Match the column of chapter MASTER PRACTICE PROBLEM of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MASTER PRACTICE PROBLEM |
| BANSAL | Match the column |
| Number Of Questions | 48 |
| Academic Year | 2023-24 |
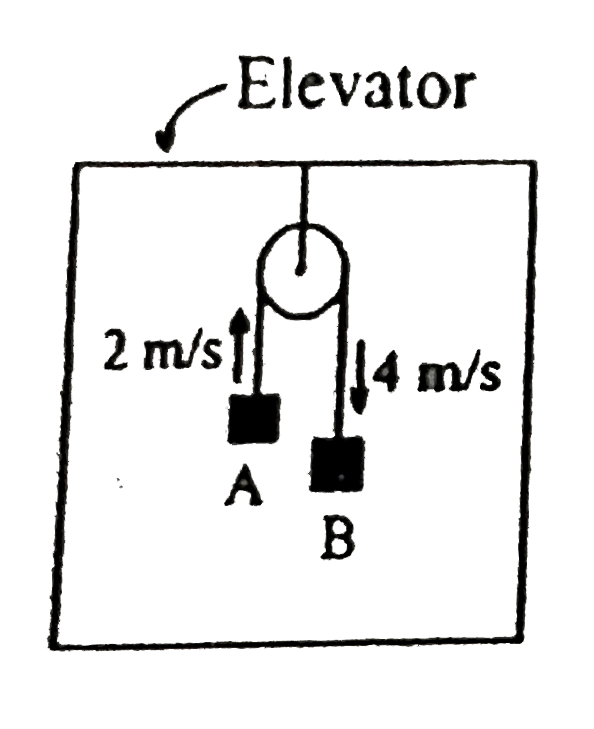
On LHS certain observations regarding a moving elevator are given. On RHS possible deductions about motion of elevator are given. More than one option may be correct
View SolutionTrajectory of a particle in a projectile motion is given by `y=x-x^(2)/80` where x and y are in meters. Match the column-1 and column-2.
`{:(,"Column-I",,"Column-II"),("(A)","x coordinate at height of 15 m",,"(P) 20 m"),("(B)",underset("point of projection at x= 100 m")"vertical distnce of particle from",,"(Q) 80 m"),("(C)","Horizontal range",,"(R) 60 m"),(,,,"(S) 25 m"):}`
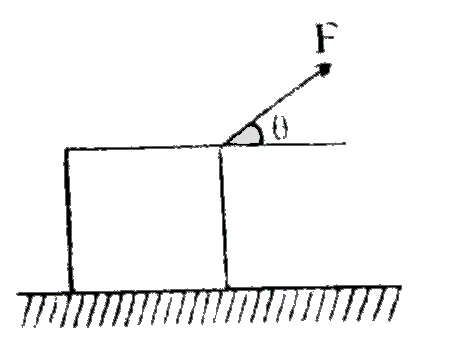
View SolutionA block is placed on a rough horizontal surface having coefficient of friction mu. A variable force `F=kt,(0 lt t lt (mg)/(ksintheta)` acts on it at an angle `theta` to

View SolutionFigure shows a block pressed against a rough vertical wall with a force F as shown in side view. Column I shows angle at which force F is applied and column -II gives information about corresponding friction force. Match them
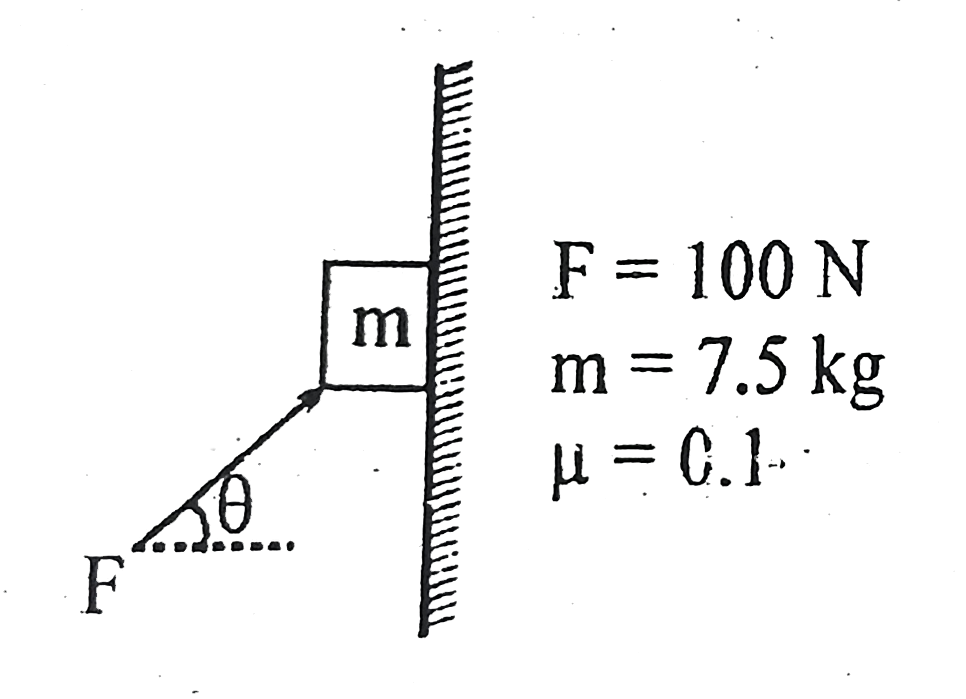
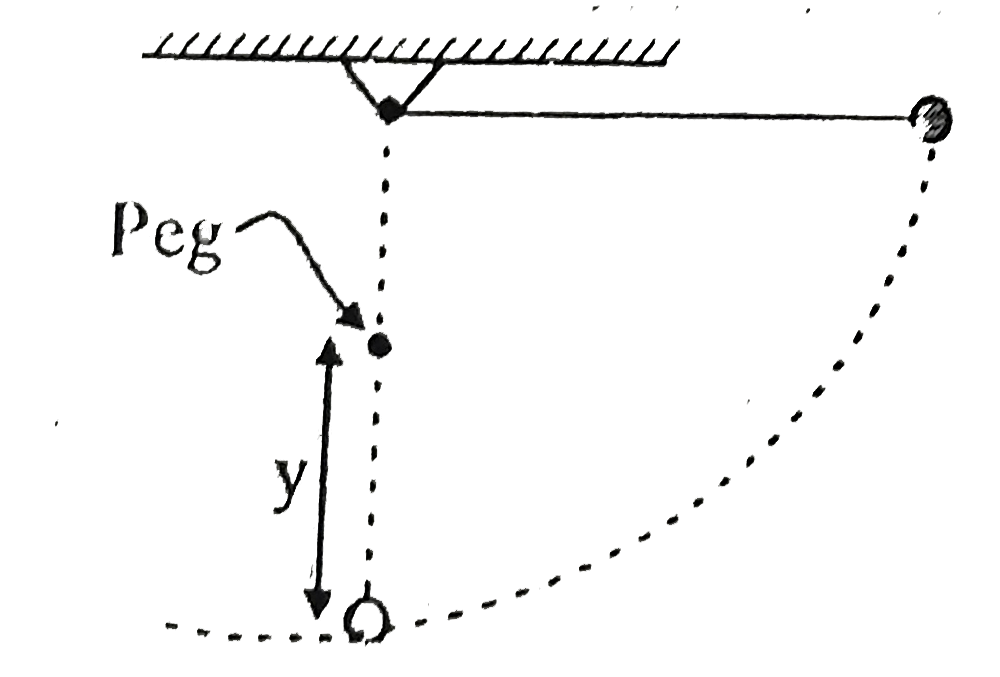
View SolutionA bob tied to an ideal string of length l is released from the horizontal position shown. A peg P whose height is adjustable, can arrest the free swing of the pendulum, as shown in Figure.
View SolutionInitially springs are in natural length. An application of external varying force F causes the block to move slowly towards the wall, on smooth floor by a distance x.
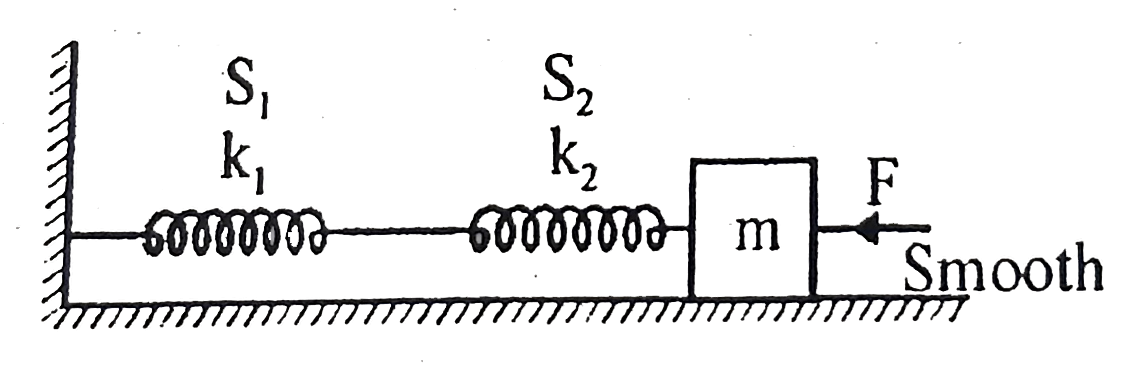
View SolutionIn the system shown, there is some friction at all surfaces but it is not sufficient to prevent slipping. Match the quantities in column I with their possible direction (s) as shown in column II.
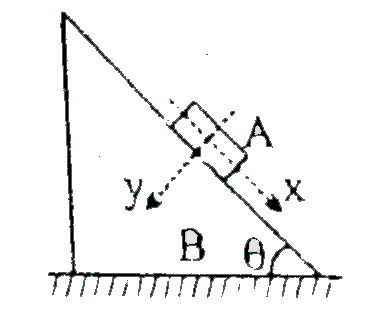
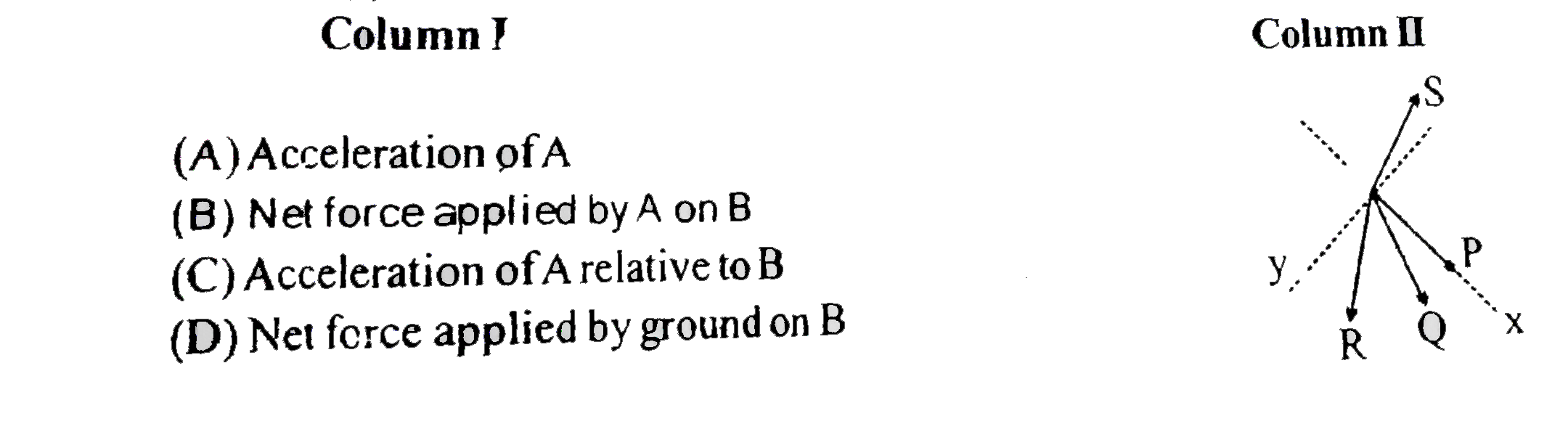
View SolutionTwo men of mass 60kg and 80 kg stand on a plank of mass 20 kg Both of them can jump with a velocity of 1 m//s relative to the plank In each event shown in column-I, match the velocity of plank after the event, given in column II

`{:(,"Column-I",,"Column-II"),("(A)","Ram alone jumps to the left",,(P)-17/40m//s),("(B)","Shyam alone jumps to the right",,(Q)-1/2m//s),("(C)",underset("jumps to right simultaneously")"Ram jumps to left and shyam",,(R)3/8m//s),(`"(D)",underset("that shyam jumps to right")"Ram jumps to left and after",,(S)-1/8m//s):}`
View SolutionIn each situation of column -I a uniform disc of mass m and radius R rolls on a rough fixed horizontal surface as shown At `t=0` (initially)the angular velocity of disc is omega_(0) and velocity of centre of mass of disc is v_(0) (in horizontal direction). The relation between v_(0) and `omega_(0)` and the initial sense of rotation is given for each situation in column-I then match the statement in column-I with the corresponding results in column-II.
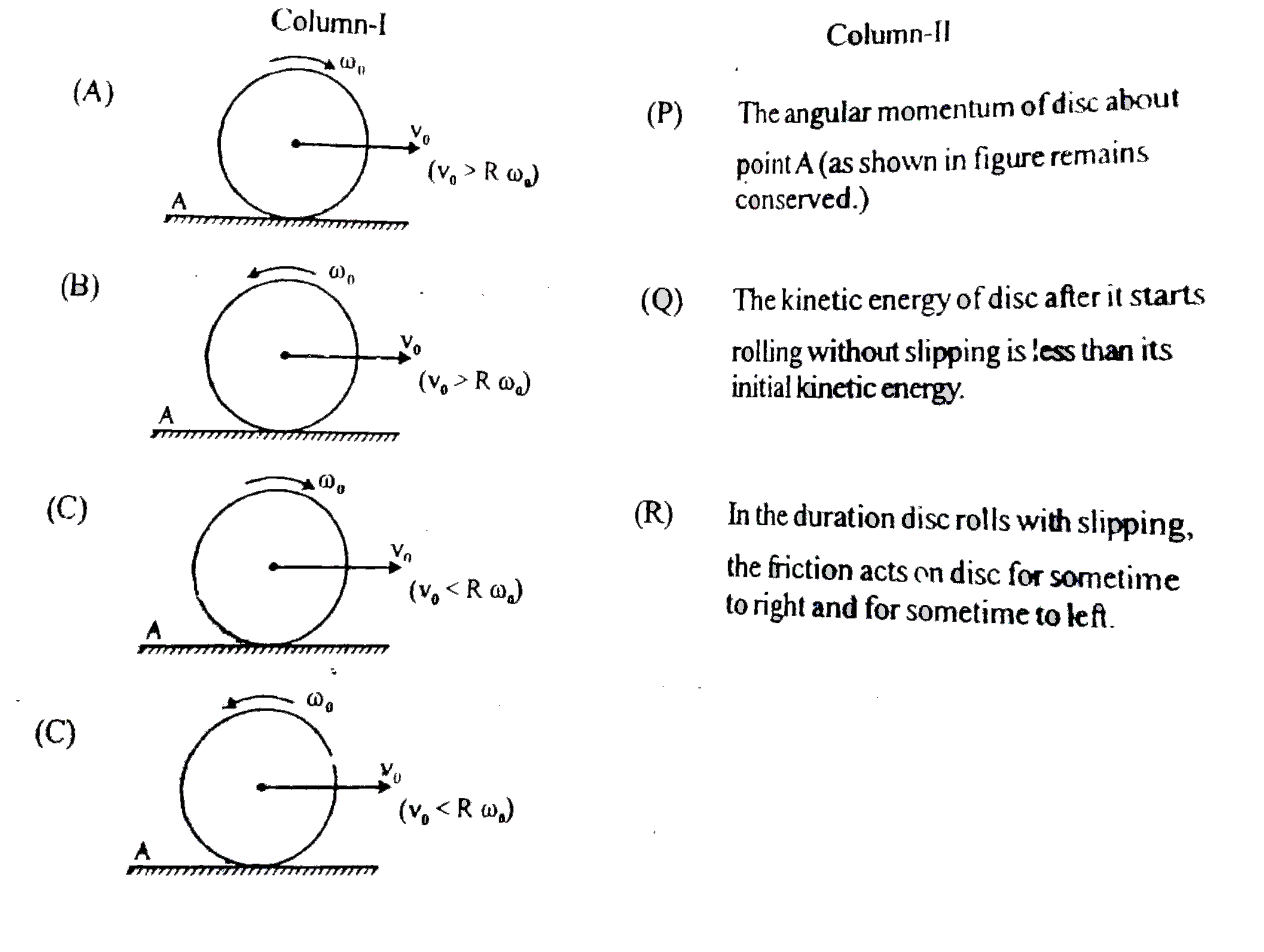
View SolutionA spool is lying on a rough horizontal surface. In the following question. Some situations, are given in column I and some conclusions or relevent data in column-II Match the columnI with column II

View SolutionA copper rod (initially at room temperature `20^(@)C`) of non-uniform cross section is placed between a steam chamber at `100^(@)C` and ice-water chamber at `0^(@)C`. `A` and `B` are cross sections are as shown in figure. Then match the statements in column -I with results in columns-II using comparing only between cross section `A` and `B`. (The mathematical expressions in column-I have usual meaning in heat transfer).
_E01_154_Q01.png)
`{:(,"Column-I",,"Column-II"),((A),"initially rate of heat flow" ((dQ)/(dt))"will be ",(p),"Maximum at section" A),((B),"At steady state rate of heat flow" ((dQ)/(dt)) "will be ",(q),"Maximum at section" B),((C),"At steady state temperature gradient" |((dT)/(dx))| "will be " ,(r),"Minimum at section B"), ((D), "At steady state rate of change of temperature"((dT)/(dt)) " at a certain point will be",(s),"Same for all section"):}`
View SolutionA satellite is a circular orbit radius 7000 km around the Earth. If it is transferred to circular orbit of double the radius,
`{:(,"Column I",,"Column II"),((A), "Angular momentum",(P),"increase."),((B),"Area of Earth covered by satellite signal",(Q),"decreases."),((C ),"potential energy",(R ),"becomes double."),((D),"kinetic energy",(S),"becomes half."):}`
View SolutionShown below is a cylinder of radius R floating in vessel containning liquids A and B Neglecting atmospheric pressure match the quantities mentioned in column-I with corresponding expression in column-II.
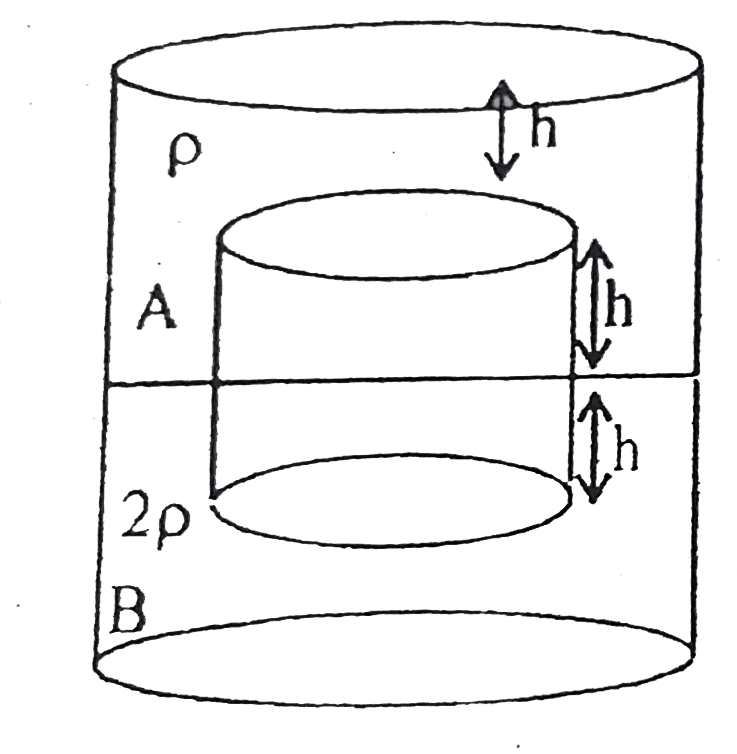
`{:(,"Column-I",,"Column-II"),("(A)",underset("density rho on the cylinder")"Net force exerted by liquid A of",,(P)9rhogRh^(2)),("(B)",underset("density 2rho on the cylinder")"Net force exerted by liquid B of",,(Q)pirhogR^(2)h),("(C)",underset("the left half of the curved part of cylinder")"Net force exerted by liquids A and B on",,(R)4pirhogR^(2)h),("(D)",underset("A and B on the cylinder")"Net force exerted by liquids",,(S)3pirhogR^(2)h):}`
View SolutionA sine wave y=sin `(2pix-2pit+pi//3)` is propagating in the medium. Match the description of the motion of particles of the medium with entries in columnI
`{:(,"Column-I",,"Column-II"),("(A)",x=1/3"m, t"=1/3sec,,"(P)Velocity is in positive y direction"),("(B)",x=1/3"m, t"=1sec,,"(Q)Velocity is in negative y direction"),("(C)",x=1"m, t"=1/3sec,,"(R)Particle is stationary"),("(D)",x=1"m, t"=1sec,,"(S)Particle has positive displacement"),(,,,"(T)Particle has negative displacement"):}`
View SolutionA small pulse travelling with speed v in a string is shown at t=0 moving towards free end. Select the shape of string column-II at moments shown in column-I

View SolutionThe graphs show the standing wave on a string at two successive instants of time `t_(1),t_(2)`.A,B,C are points on the string (S_(0) is the maximum displacement amplitude of the standing wave) column-II gives observations about net mechanical energy for the time interval between t_(1) & t_(2) Match the column
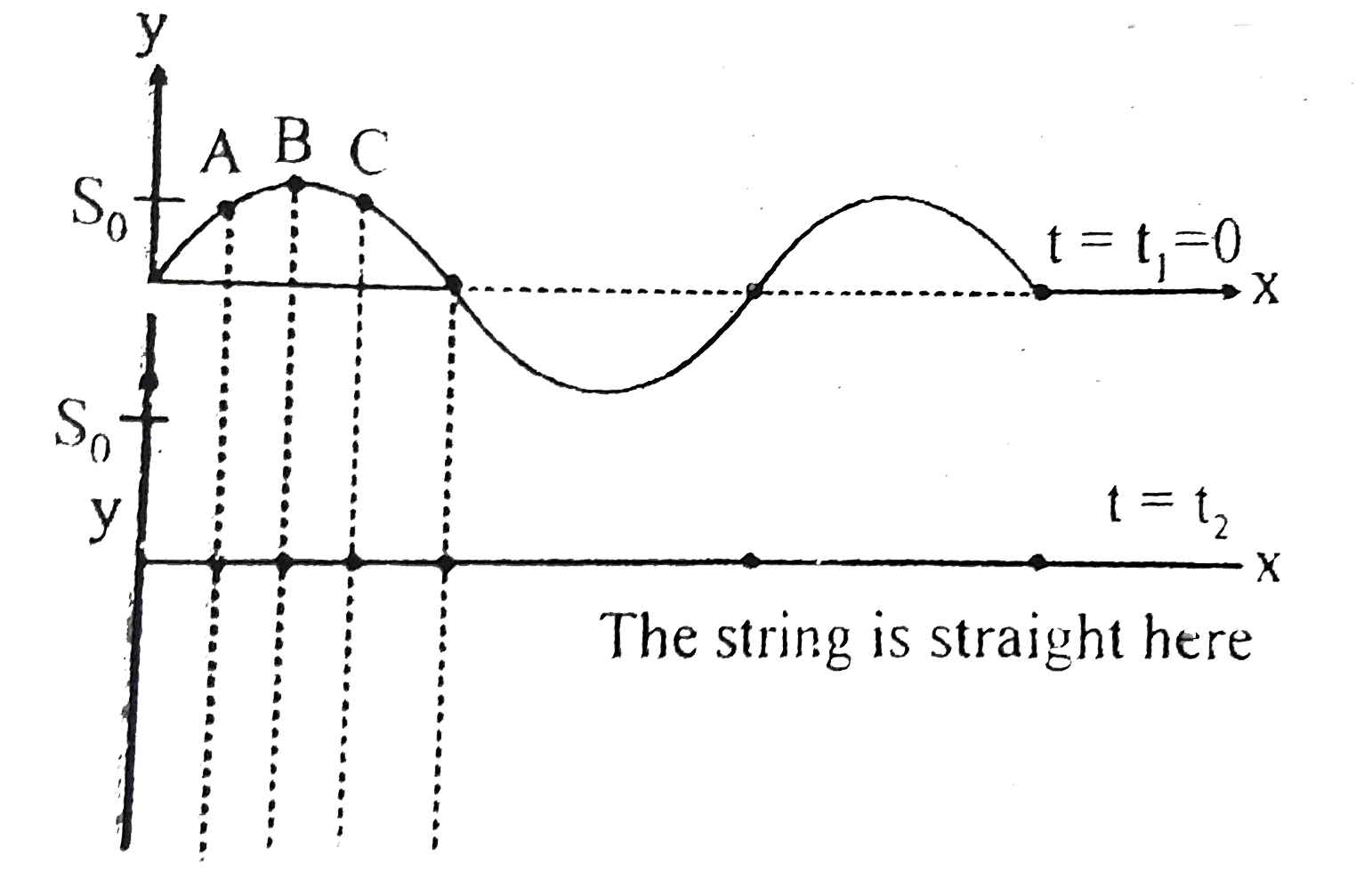
`{:(,"Column-I",,"Column-II"),("(A)","A",,"(P)kinetic energy at this element is increasing"),("(B)","B",,"(Q)Energy is flowing towards right through this point"),("(C)","C",,"(R)Energy is flowing left through this point"),(,,,"(S)No net energy ever crosses this point"):}`
View SolutionSound is travelling in a long tube towards right and the graph of excess pressure variation Vs position (at some instant) is given below.
 Match velocities in column-I with column-II P,Q,R,S,T are medium particles inside the tube.
Match velocities in column-I with column-II P,Q,R,S,T are medium particles inside the tube.
`{:(,"Column-I",,"Column-II"),("(A)","velocity is towards right",,"(P)P"),("(B)","velocity is towards left",,"(Q)Q"),("(C)","velocity is zero",,"(R)R"),("(D)","Speed is maximum",,"(S)S"),(,,,"(T)T"):}`
View Solution
Observers `O_(1) and O_(2) ` are at rest and the wall is moving with velocity V_(w) Cart is moving with constant velocity V_(s) towards wall. The source of sound is in the cart, the original frequency of the wave is f. sound has velocity C w.r.t. ground (medium is stationary) Then match the column -I with column-II
`{:(,"Column-I",,"Column-II"),("(A)","Wavelength received by" O_(1) "directly from cart",,"(P)"((C-V_(w))/(C+V_(w)))((C-V_(s)))/f),("(B)","Wavelength received by" O_(2) "directly from cart",,"(Q)"(C+V_(s))/f),("(C)",underset("after reflection from wall")"Wavelength received by driver of the cart",,"(R)"((C+V_(w))/(C-V_(w)))((C-V_(s)))/f),("(D)",underset("reflection from wall")"Wavelength received by" O_(1) "after",,"(S)"(C-V_(s))/f),(,,,"(T)None of these"):}`
View Solution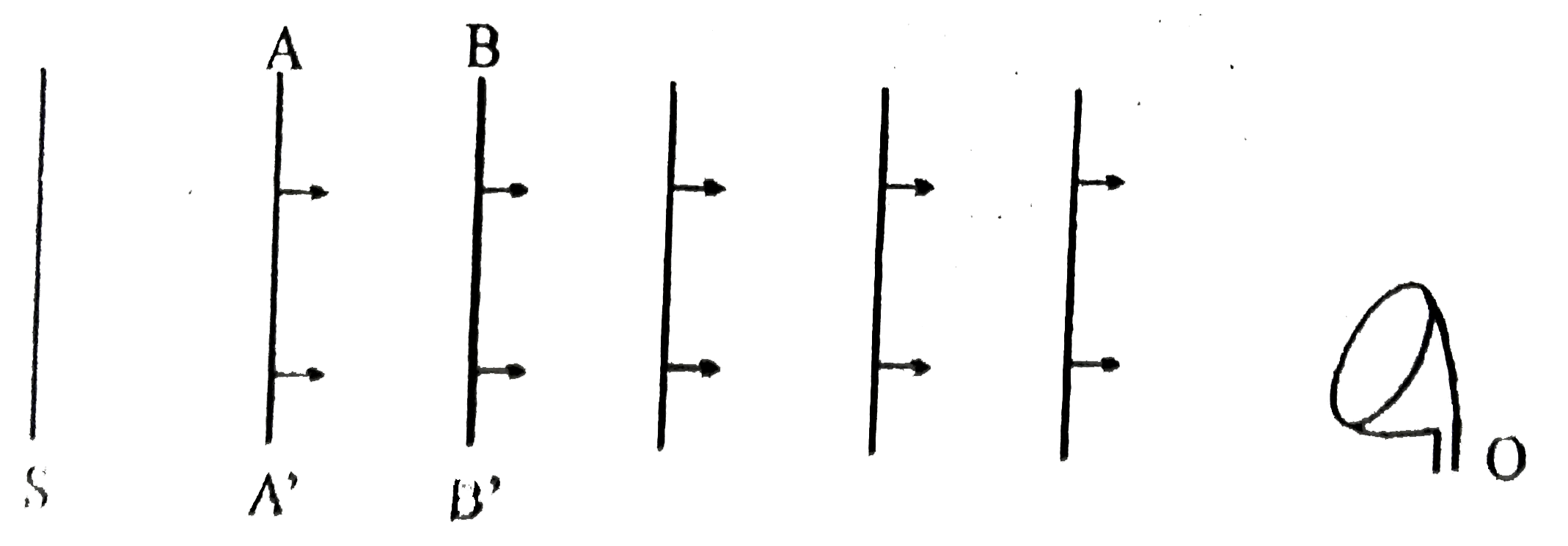
The diagram shows plane wavefronts for sound wave travelling in air towards right Each of these wavefronts represent successive pressure maxima for the pressure wave. Initally the source S, observer O and medium are all at rest. The source is a large plane diaphragm and observer is a detector Wave fronts being considered in column-II have been emitted after the action in column-II has taken place.
`{:(,"Column-I",,"Column-II"),("(A)","Source starts moving towards right",,"(P)distance between any two wavelength will increase"),("(B)","Air starts moving towards right",,"(Q)distance between any two wavefronts will decrease"),("(C)",underset("towards left with same speed")"Observer and source both move",,underset("point A to B in space will increase")"(R)the time needed by sound to move"),("(D)",underset("move towards right with same speed")"Source and medium air both",,underset("point A to B in spce will decrease")"(S)time needed by sound to move from"),(,,,"(T)frequency received by observer is increase"):}`
View SolutionEntries in column I consist of diagrams of thermal conductors. The type of conductor & direction of heat flow are listed below Entries in column-II consist of the magnitude of rate of heat flow belonging to any of the entries in column I if temperature difference in all the cases is `(T_(1)-T_(2))` then match the columns
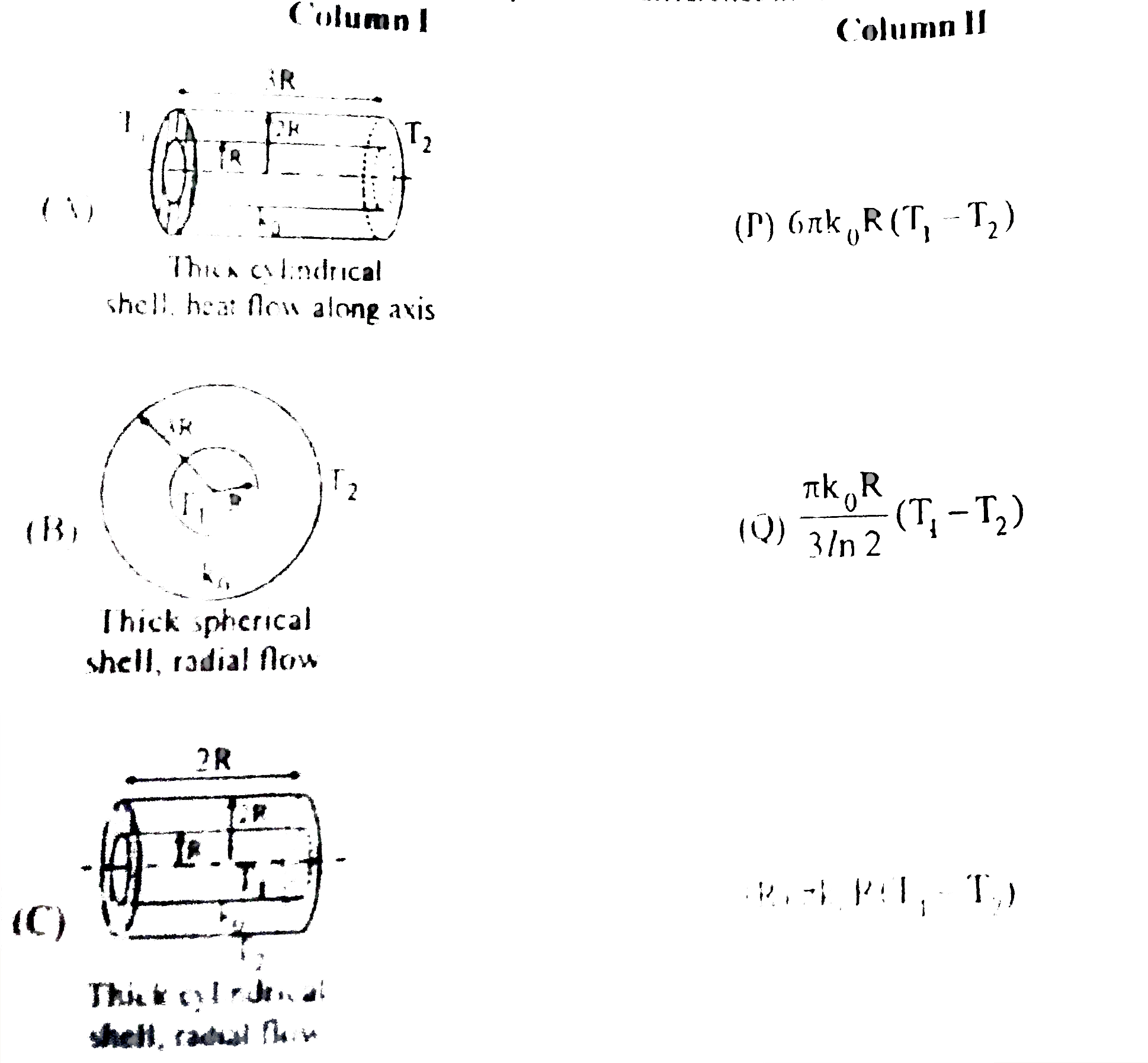

View SolutionIn column-I some situations have been described and in column-II corresponding graph is given. Match the entries in column-I with appropriate entries in column-II.
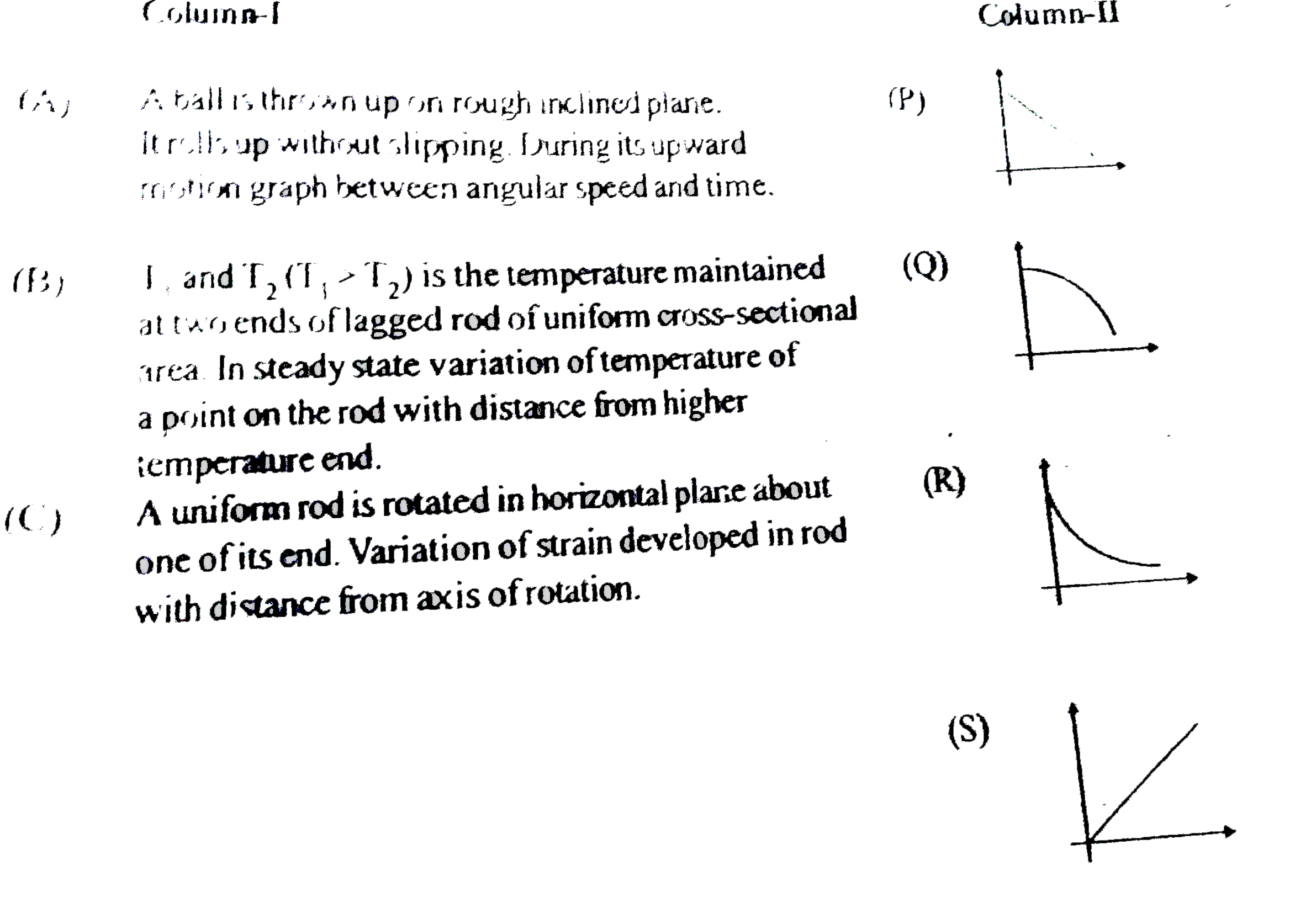
View SolutionWe have three solid bodies of same material A rightarrow a solid cube of edge length 'r' Brightarrow a solid sphere of radius 'r' and C rightarrow a solid hemisphere of radius 'r' In coloumnI certain situation related to these bodies are given Match the appropriate outcome indicated in column-II
`{:(,"Column-I",,"Column-II"),("(A)",underset("300k Then rate of fall of temperature with time")"All 3 bodies are heated to some temperature of 350k and kept in a room at",,"(P)for C is highest" "(Q)for B is highest"),("(B)",underset("C is kept with base on ground height of centre of mass from ground")"All 3 bodies are kept on level ground",,"(R)for C is lowest"),("(C)",underset("for cube and hemisphere is perpendicular to the fase and base respectively Moment of inertia")"All 3 bodies are rotated about an axis passing through their repective centre of mass the axis",,"(S) for one of the body is half of another body"):}`
View SolutionIn each situation of column-I a process A rightarrow B rightarrow C is given for an ideal gas. Match each situation of column-I with correct result in column II

View SolutionA spherical metallic conductor has a spherical cavity. A positive charge is placed inside the cavity at its centre. Another positive charge is placed
View SolutionColumn I shows graphs of electric potential V versus x and Y in a certain region for four situations Column II shows the range of angle which the electric field vector makes with positive x-direction.

View SolutionA circuit involving five ideal cells, three resistance (R_(1),R_(2) and 20Omega) and a capacitor of capacitance `C=1 mu F` is shown Match the conditions in column-I with results given in Column-II [Assuming circuit is in steady state]
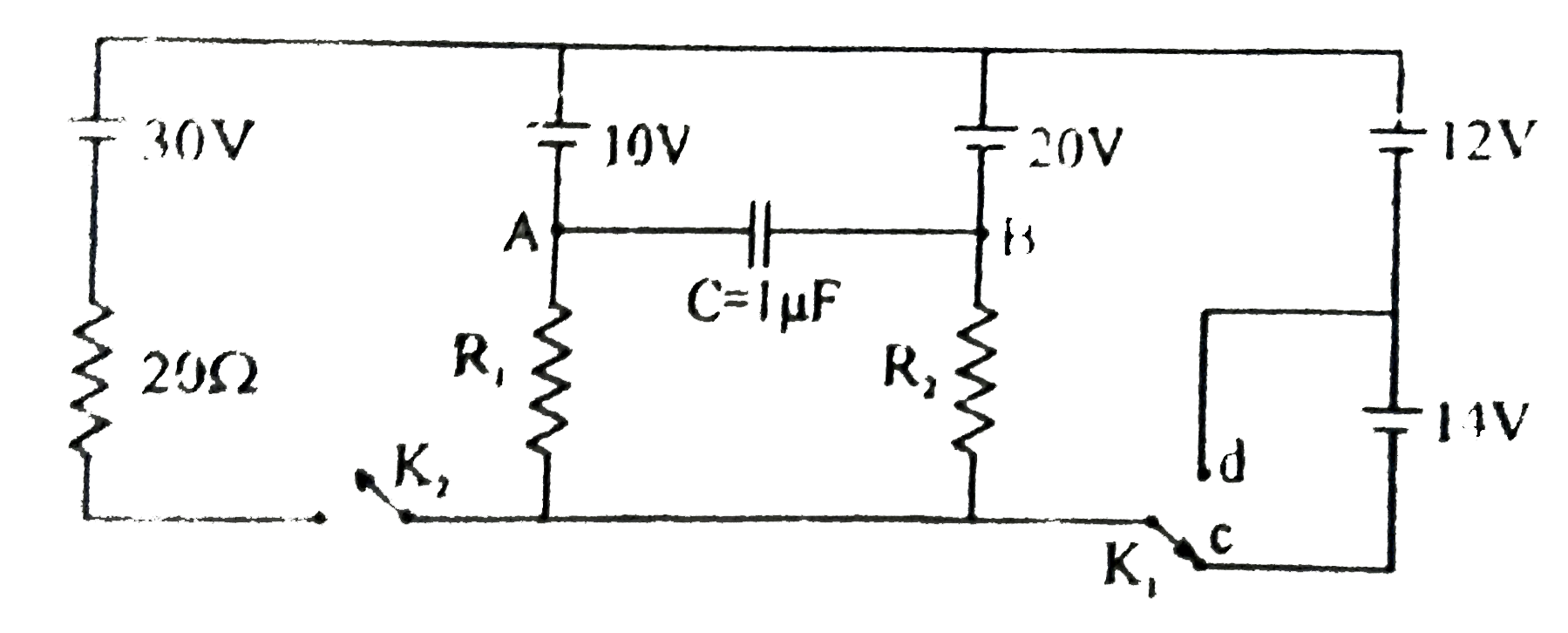
`{:(,"Column-I",,"Column-II"),("(A)",K_(2) " is open and " K_(1) " is in position C",,"(P)Potential at point A is greater then potential at B"),("(B)",K_(2) " is open and " K_(1) " is in position D",,"(Q)Current through " R_(1) " is downward"),("(C)",K_(2) " is closed and " K_(1) " is in position C",,"(R)Current through " R_(2) " is upward"),("(D)",K_(2) " is closed and " K_(1) " is in position D",,"(S)Charge on capacitor is 10 "mu"C"):}`
View SolutionIn the circuit, both capacitors are identical. Column-I indicates action done on capacitor and Column II indicates effect on capacitor 2. Select correct alternative.
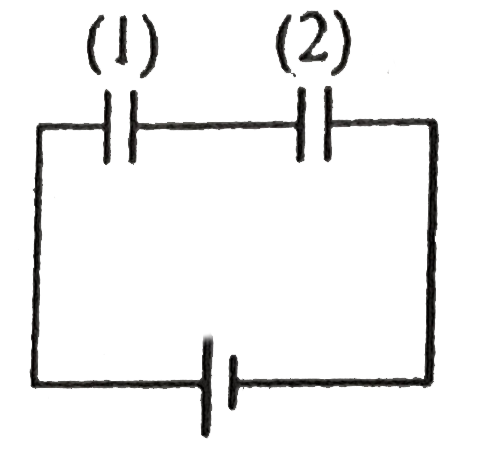
`{:(,"Column-I",,"Column-II"),("(A)","Plates are moved further apart",,"(P)Amount of charge on left plate increases"),("(B)","Area increased",,"(Q)Potential difference increases"),("(C)","Left plate is earthed",,"(R)Amount of charge on right plate decreases"),("(D)","It's plates are short circuited",,"(S)None of the above effects"):}'
View SolutionSome events related to a capacitor are listed in column-I Match these events with their effect (s) is column-II
`{:(,"Column-I",,"Column-II"),("(A)","Insertion of dielectric while battery remain attached",,"(P)Electric field between plates changes"),("(B)","Removal of dielectric while battery is not present",,"(Q)Charge present on plates changes"),("(C)","Slow decrease in separation between plates while battery is attached",,"(R)Energy stored in capacitor increases"),("(D)","Slow increase of separation between plates while battery is not present",,"(S)Work done by external agent is positive"):}'
View Solution`{:(,"Column-I",,"Column-II"),("(A)",underset("Plate air core capacitor are slowly pulled apart")"Plates of an isolated charged parallel",,underset("increases in the process")"(P)Electric energy stored inside capacitor increases in the process"),("(B)",underset("air cored capacitor to completely fill the space between plates")"A dielectric is slowly inserted inside an isolated and charged parallel plate",,underset("capacitor remain unchanged")"(Q)Force between the two plates of the"),("(C)",underset("connected across a battery are slowly pulled apart")"Plates of a parallel plate capacitor",,underset("plates remain unchanged")"(R) Electric field in the region between"),("(D)",underset("a battery to completely fill the space between plates")"A dielectric slab is slowly inserted inside a parallel plate capacitor conneted across",,underset("capacitor decreases in the process")"(S)total electric energy stored inside"),(,,,"(T)Electriec field in the region between plates decreases"):}`
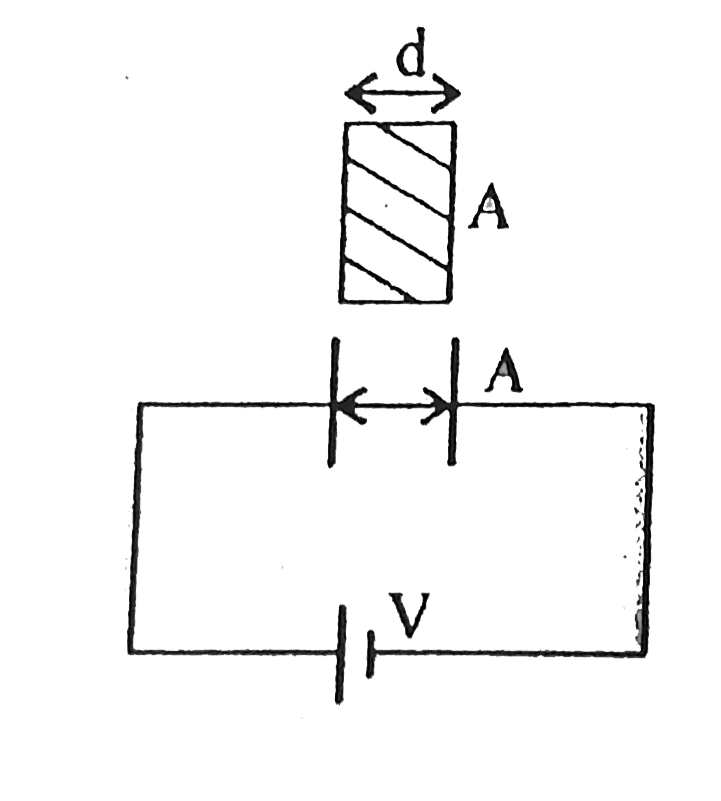
View SolutionColumn I gives physical quantities based on a situation in which an ideal cell of emf V is connected across a cylindrical rod of uniform cross-section area and conductivity (sigma) as shown in figure E, J, phi and I are electric field at, current density through, electric flux through and current through shaded cross section repectively as shown in figure. Physical quantities in column-II are equal to those in column i Match the expression in Column I with the statement in Column II
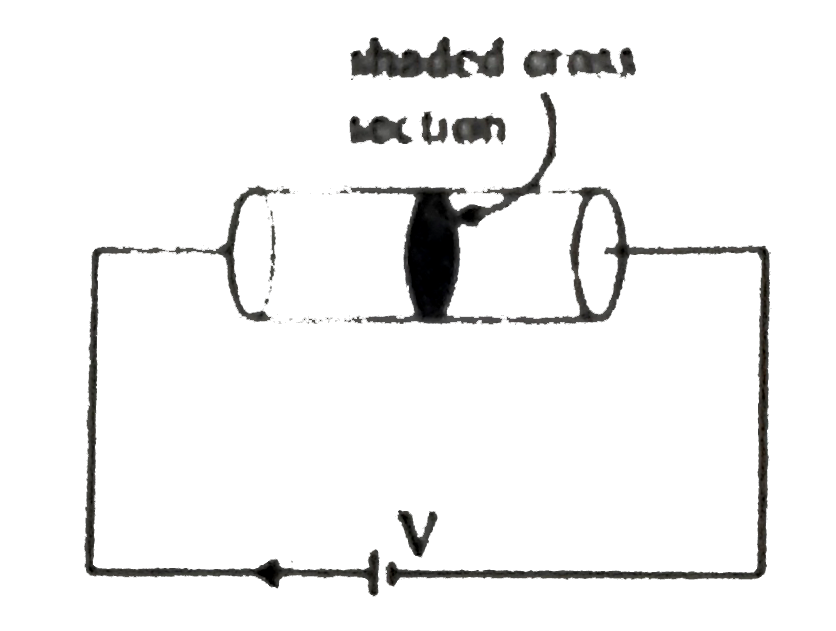
`{:(,"Column-I",,"Column-II"),("(A)",phi/i,,"(P)Conductivity of rod"),("(B)",E/J,,"(Q) Resistance of rod"),("(C)",sigma phiV,,"(R)Resistivity of rod"),("(D)",V/sigmaphi,,"(S)Power delivered to rod"):}`
View SolutionA charged particle having non zero initial velocity is subjected to certain conditions given in column -I column-II gives possible trajectories of the particle Match the conditions in column-I with the results in column-II
`{:(,"Column-I",,"Column-II"),("(A)","In only uniform electric field",,"(P)the path of the charged particle may be a straight line"),("(B)","in only uniform magnetic field",,"(Q)the path of the charged particle may be a parabola"),("(C)","in uniform magnetic and uniform electric field",,"(R)the path of the charged particle may be circular"),("(D)","Subjected to a net force of constant magnitude",,"(S)the path of the charged particle may be helical with uniform pitch"),(,,,"(T)the path of the charged particle may be helical with non uniform pitch"):}`
View SolutionColumn-I shows some charge distributions and current distributions accompanied by their descriptions Column-II shows the instantaneous characteristic Here alpha symbolizes the system on which results are to be obtained.

View SolutionColumn I shows four current configurations Match each entry of column I with those axes in column II along which the magnetic field at origin has positive component

View Solutionin column - I certain situations are shown Column-II has different values of phase difference Match them [take `pi^(2)=10` wherever required]


View SolutionColumn-I describe the value of variables indicated in column-II Assume potential energy in gravitation and electrostatics to be zero at infinity if the quantity mentioned in columnII is a vector positive and negative refer to the direction and increasing or decreasing refer to magnitude Match the appropriate entries.
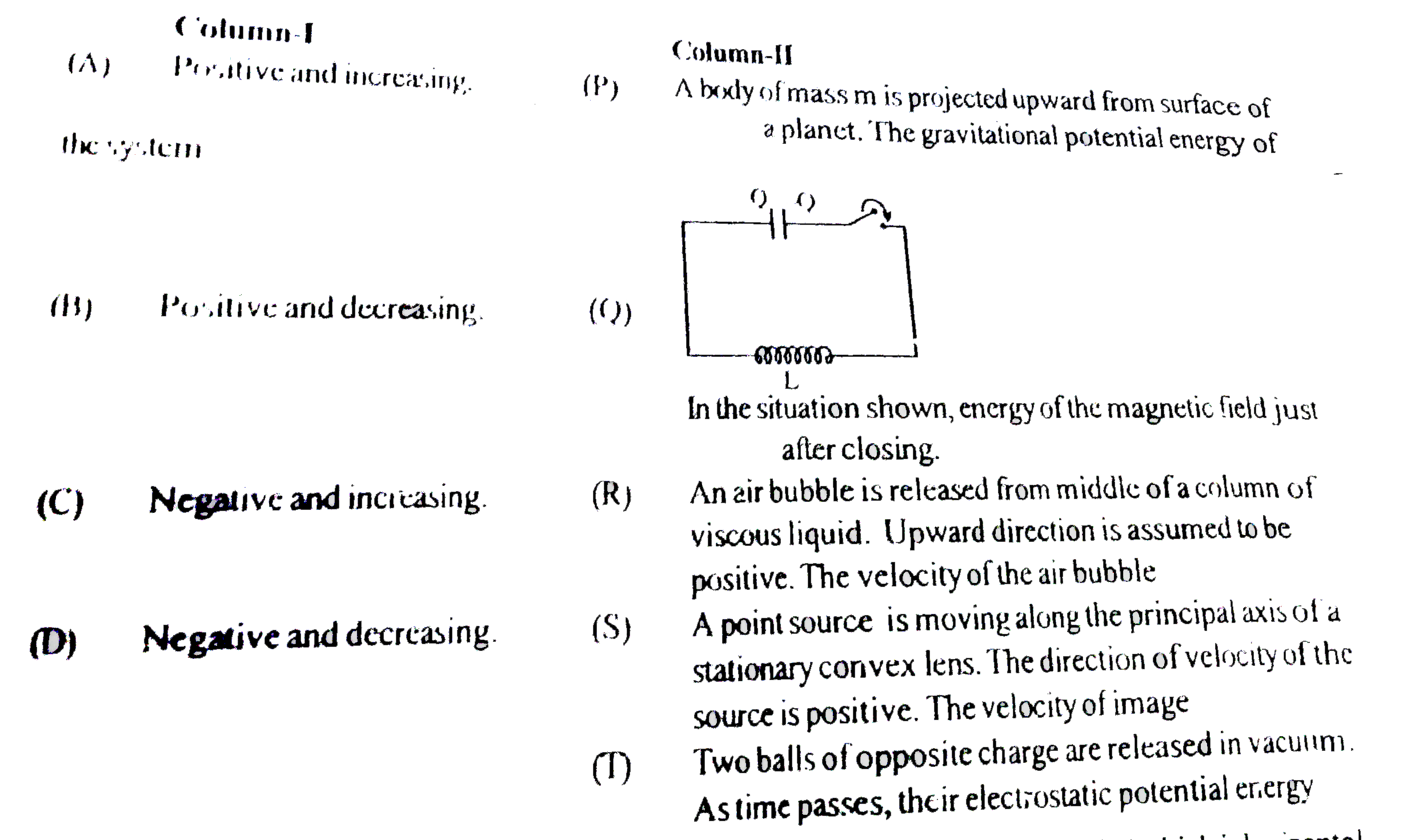
View SolutionA homogeneous magnetic field B is perpendicular to a sufficiently long trach of width l which is horizontal A frictionless conducting resistanceless rod of mass m stradless the two rails of the track as shown in the figure. Entire arrangement lies in horizontal plane. For the situation suggested in column-II match the appropriate entries in column-I the rails are also resistancesless.


View SolutionA spherical fish bowl of radius R is placed in front of a plane vertical mirror (M) The thickness of the wall of the fish bowl is very thin The centre (C) of the spherical bowl is at distance of 3R from the plane mirror. The bowl is filled with water and contains a fish (F) Fish(F) is at a distance of R from the centre of the spherical bowl as shown in the figure Refractive index of water is 4/3 two surfaces are indicated in the bowl as first surface (1) and second surface(2)

`{:(,"Column-I",,"Column-II"),(,ul("Optical Event"),,ul("Nature of image")),(,"(A)Refraction at first surface",,"(P)Virtual"),(,"(B)Refraction at second surface after reflection from mirror",,"(Q)Real"),(,underset("from mirror and refraction from second surface")"(C)Refraction at first surface after reflection",,"(R)Magnified"),(,,,"(S)Diminished"):}`
View SolutionConsider the situation shown in column-I a real object is moving towards a fixed optical component or an optical component is moving towards a fixed object. Match the possible direction and magnitude to velocity of image as shown in Column-II (All velocities in column-II are equal to v_(0))

View SolutionLight is incident at surface PQ of prism as shown in column I then match the column I with column II (Surrounding medium is air in all cases)

View SolutionAn extended object is moving in front of concave mirror as shown in figure On L.H.S velocity of object and position is given On R.H.S some properties of image and its velocity is given Consider velocity along x-axis only

`{:(,"Object",,"Image"),("(A)","+ve velocity and object is between focus and centre of curvature",,"(P)+ve velocity"),("(B)","-ve velocity and object is between focus and pole",,"(Q)-ve velocity"),("(C)","-ve velocity and object is beyond centre of curvature",,"(R)size of image is increasing"),("(D)","-ve velocity and object is virtual",,"(S)size of image is decreasing"):}`
View SolutionA bird in air is diving vertically over a tank with speed 6 cm//s Base of the tank is silvered A fish in the tank is rising upward along the same line with speed 4 cm//s[Take:mu_(water)=4//3]

`{:(,"Column-I",,"Column-II"),("(A)","Speed of the image of fish as seen by the bird directly",,"(P)12"),("(B)",underset("from the mirror as seen by the bird")" Speed of the image of fish formed after reflection",,"(Q) 4"),("(C)","Speed of image of bird relative to the fish looking upwards",,"(R) 9"),("(D)",underset("downwards in the mirror")" Speed of image of bird relative to the fish looking",,"(S) 3"):}`
View SolutionIn a standard Yound's Double Slit Experiment light of wavelength `lambda=6000A` is used screen distance (D)=1m and slit separation (d)=`0.5` mm intensity of light on screen emerging from slits are individually I_(0) and 4I_(0) Column I indicates distance of certain point P on screen from central maxima Match the columns
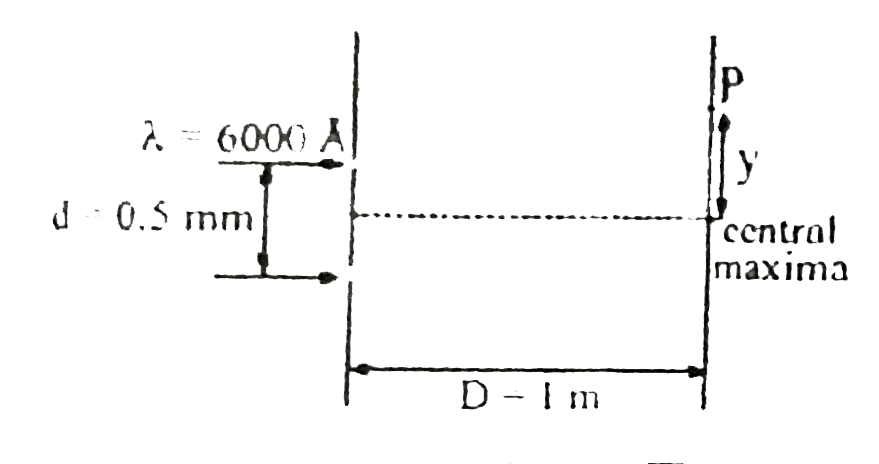
`{:(,"Column-I",,"Column-II"),("(A)","y=2 mm",,"(P)Intensity = 7" I_(0) "at P"),("(B)","y=2.2 mm",,"(Q)Intensity =3" I_(0) "at P"),("(C)","y=2.6 mm",,"(R)P lies between" 2^(nd) "minima and" 3^(rd) "maxima"),("(C)","y=2.6 mm",,"(S)P lies between" 3^(rd) "minima and" 2^(nd) "maxima"):}`
View SolutionA ray of light is incident on a thin film Two of the reflected rays are shown, and two of the transmitted rays are shown in figure. Consider phase difference by comparing them with the phase of incident ray on the film. Match statements about phase difference in column-I with the correct order of refractive indices in column -II
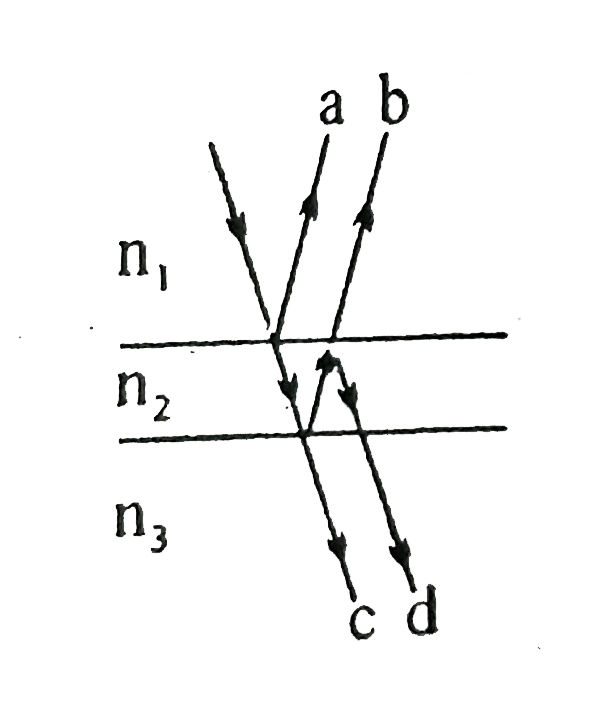
`{:(,"Column-I",,"Column-II"),("(A)",underset("and above that due to extra optical path caused by reflection at various interfaces")"Rays a and b have an extra phase difference over",,(P)n_(1)gtn_(2)gtn_(3)),("(B)",underset("and above that due to extra optical path caused by reflection at various interfaces")"Rays a and c have an extra phase difference over",,(Q)n_(2)gtn_(3)gtn_(1)),("(C)",underset("and above that due to extra optical path caused by reflection at various interfaces")"Rays a and d have an extra phase difference over",,(R)n_(3)gtn_(2)gtn_(1)),("(D)",underset("and above that due to extra optical path caused by reflection at various interfaces")"Rays b and c have an extra phase difference over",,(S) n_(1)=n_(3)gtn_(2)),(,,,"(T)the specified extra phase difference is not possible"):}`
View SolutionLight from sources `S(|u|lt|f|)` falls on lens and screen is placed on the other side the lens is formed by cutting it alond principal axis into two equal parts and are joined as indicated in column II
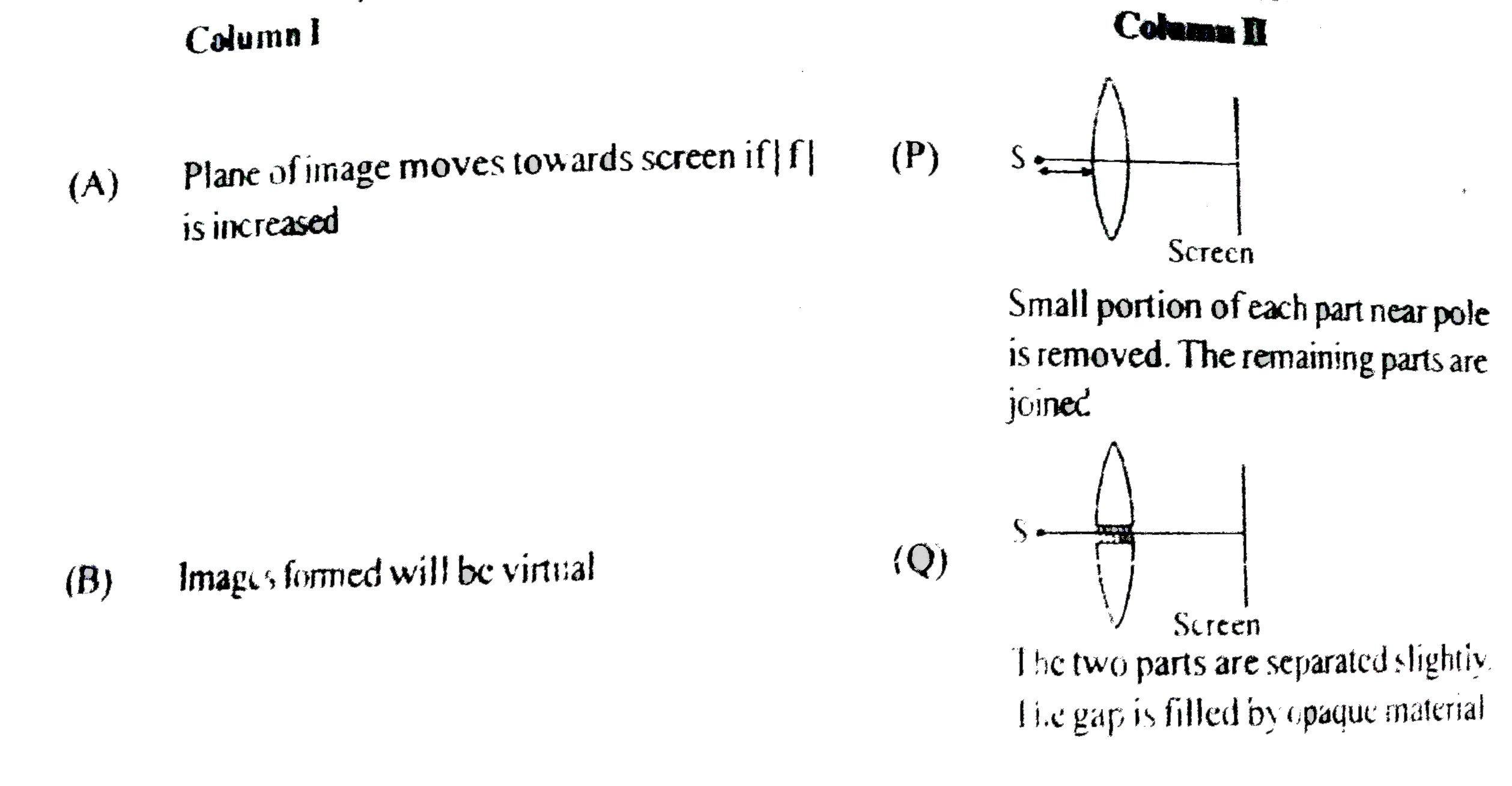

View SolutionThree physical quantities are listed in column I and their values are listed in column II in random order Match the oppropriate quantities.
`{:(,"Column-I",,"Column-II"),("(a)","binding energy of heavy nuclei per nucleon",,"(1) 10 keV"),("(b)","X-ray photon energy",,"(2) 7 MeV"),("(c)","Photon energy of visible light",,"(3) 2 eV"):}`
View SolutionThen choose the correct option in which matching is correct


View Solution`{:(,"Column-I",,"Column-II"),("(A)","beta-rays",,"(P)Continous energy distribution with dark lines in between"),("(B)","y-rays",,"(Q)Continuous energy distribution with sharp peacks in between"),("(C)","Absorption spectrum of Hydrogen",,"(R)Continuous energy distribution"),("(D)","X-rays",,"(S)Discrete energy distribution"):}`
View SolutionQ is energy released in the decay m_(x) is atomic mass of parent nucleus m_(y) is atomic mass of daughter nucleus and m_(e) is mass of elctron then match the following:
`{:(,"Column-I",,"Column-II"),("(A)","k capture",,(P) Q=(m_(x)-m_(y))c^(2)),("(B)",beta^(-) decay,,(Q)Q=(m_(x)-m_(y)-m_(c))c^(2)),("(C)",beta^(+) decay,,(R)Q=(m_(x)-m_(y)-2m_(e))c^(2)),(,,,(S)Q=(m_(x)-m_(y)+2m_(e))c^(2)),(,,,):}`
View Solution
Match the column questions and complete solutions for chapter MASTER PRACTICE PROBLEM of BANSAL MATHS (HINGLISH) of Class 12