Complete Solutions to ILLUSTRATIONS of chapter GRAPHS OF ELEMENTARY FUNCTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | GRAPHS OF ELEMENTARY FUNCTIONS |
| CENGAGE NEW | ILLUSTRATIONS |
| Number Of Questions | 80 |
| Academic Year | 2023-24 |
The equation of a tangent to the parabola `y^2=""8x""i s""y""=""x""+""2` . The point on this line from which the other tangent to the parabola is perpendicular to the given tangent is (1) `(-1,""1)` (2) `(0,""2)` (3) `(2,""4)` (4) `(-2,""0)`
View SolutionDraw the graph of `f(x) = (x^(3)-x)/(x^(2)-1)`.
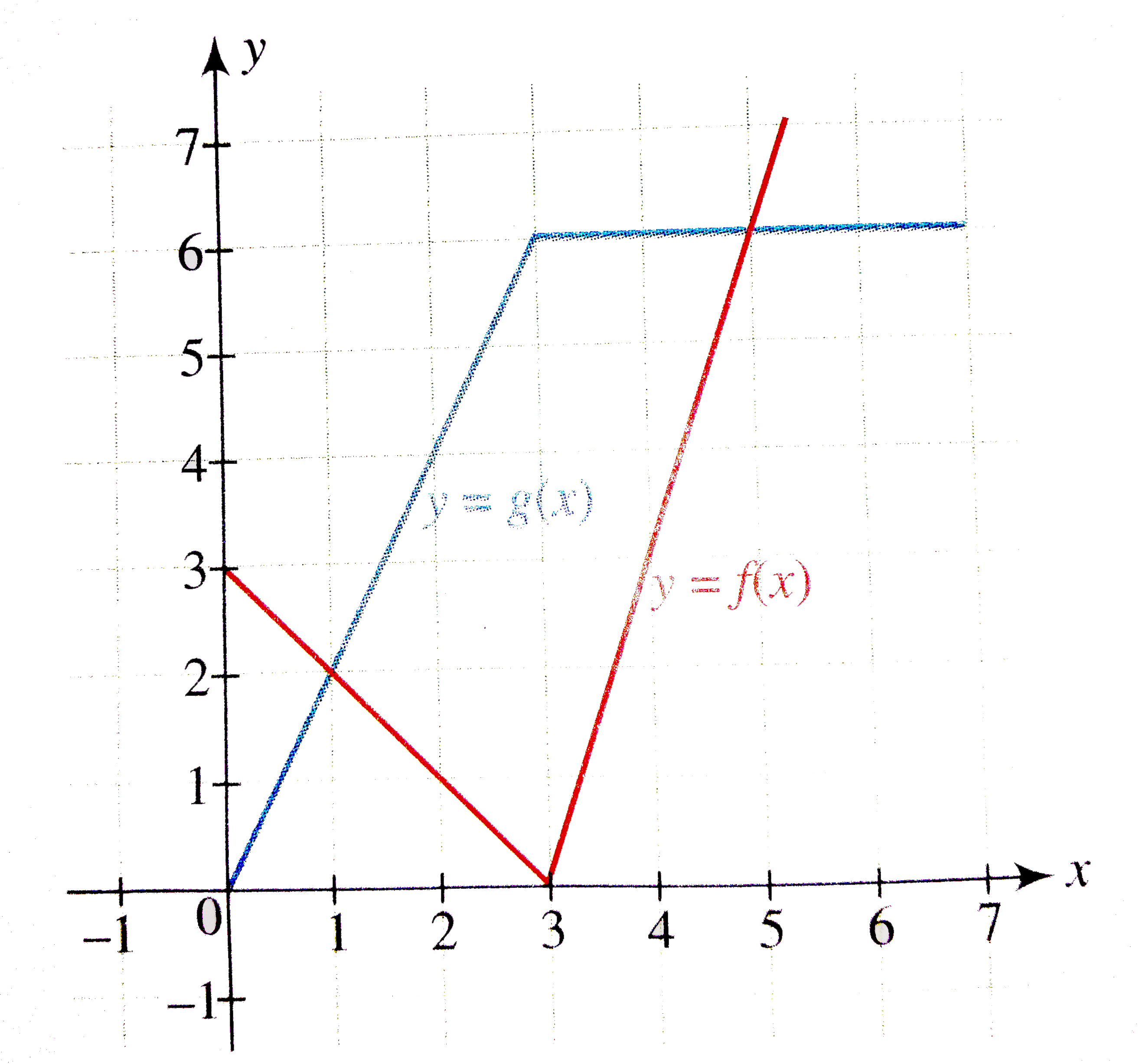
View SolutionGraph of `y=f(x) and y=g(x)` is given in the following figure. If `h(x)= f(g(x))`, then find the value of `h'(2)`.
View SolutionLet `f(x) = (1 - x)^2 sin^2 x + x^2 ` for all x ∈ R, and let `g(x) = ∫((2(t - 1))/(t + 1) - ln t)f(t)dt` for t ∈ [1, x] for all x ∈ (1, ∞).Which of the following is true ?
View SolutionSketch the regions satisfying the following inequalities:
(a) `x gt 2`
(b) `|y| ge 1`
View SolutionShade the regions where points satisfy `|x-y| lt 1`.
View SolutionPlot the region satisfying `|x|+ |y| le 2 and |x|+|y| gt 2`.
View SolutionIf `x lt 2`, then find the values of `x^(2)` graphically.
View SolutionIf `x lt -1`, then find the values of `x^(2)` graphically.
View SolutionDraw the graph of `f(x) = {{:(x^(3)","x^(2) lt 1), (x","x^(2) ge 1):}`
View SolutionIf `x gt 2`, then find the values of `1//x` graphically.
View SolutionIf `x lt -1`, then find the values of `1//x` graphically.
View SolutionWhen `x gt -2`, find the values of `1//x`.
View SolutionWhen `x lt 3`, find the values of `1//x`.
View SolutionDraw the graph of `(1)/(x)+ (1)/(y)=1`.
View SolutionDraw the graph of `y=(1)/(x^(2))`.
View SolutionDraw the graphs of following quadratic functions.
(i) `y=x^(2)+x+1" "` (ii) `y=x^(2)-2x-3`
(iii) `y=2+x-x^(2)" "`(iv) `y=x-1-x^(2)`
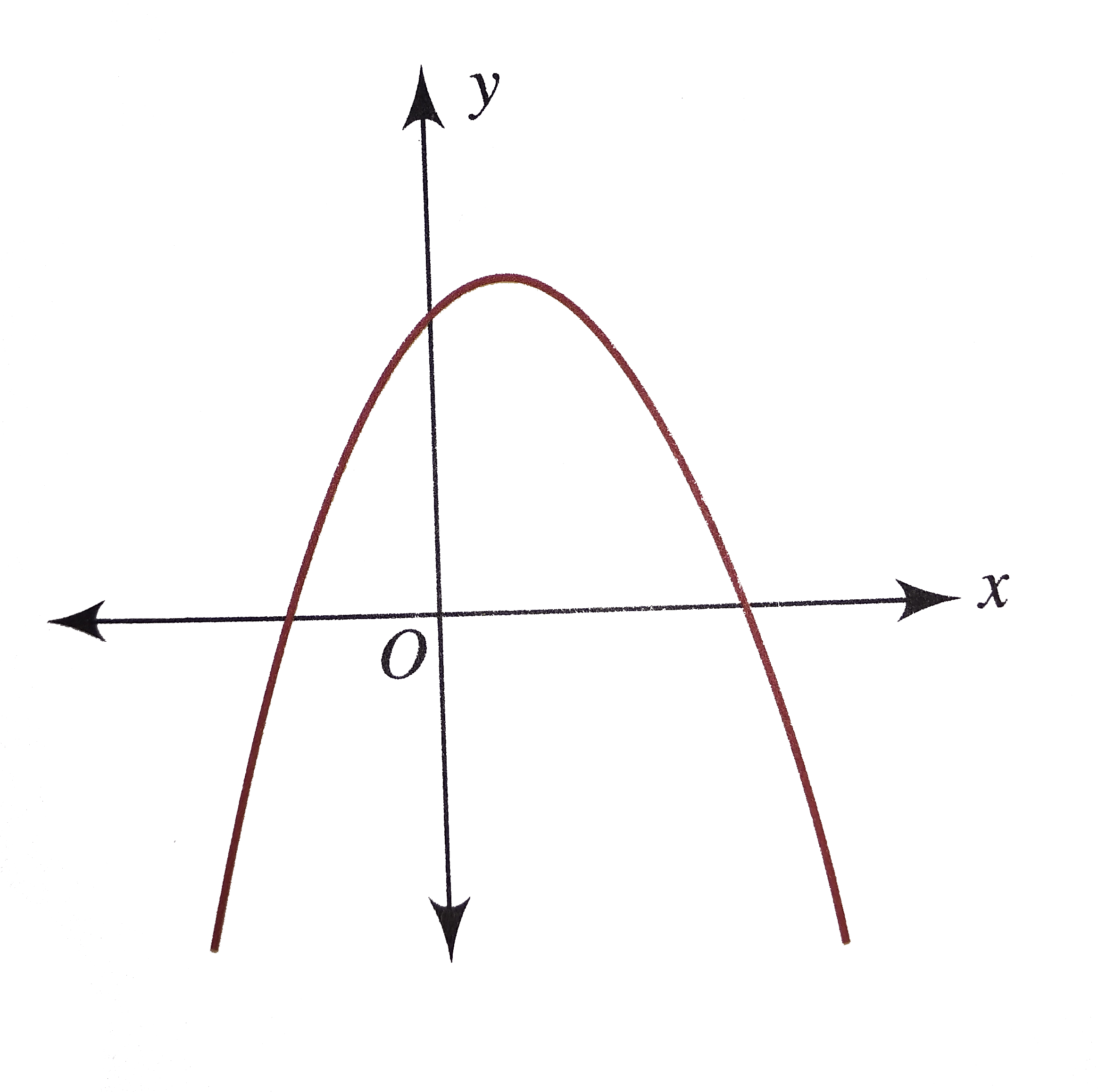
View SolutionThe following figure shows the graph of `f(x)= ax^(2)+ bx+c`, find the signs of `a, b and c`.
View SolutionLet `f(x)=2x(2-x), 0 le x le 2`. Then find the number of solutions of `f(f(f(x)))= (x)/(2)`.
View Solution`f:R to R` is defined as `f(x)= {{:(x^(2)+kx+3",",,"for "xge0),(2kx+3",",,"for "x lt0):}`. If `f(x)` is injective, then find the values of `k`.
View SolutionIf `f(x)=x^3+4x^2+lambdax+1` is a monotonically decreasing function of `x` in the largest possible interval `(-2,-2/3)dot` Then (a)`lambda=4` (b) `lambda=2` `lambda=-1` (d) `lambda` has no real value
View SolutionFor what real values of `a` do the roots of the equation `x^2-2x-(a^2-1)=0` lie between the roots of the equation `x^2-2(a+1)x+a(a-1)=0.`
View SolutionFind the value of `a` for which `a x^2+(a-3)x+1 < 0` for at least one positive real `x`.
View SolutionConsider the inequation `9^(x) -a3^(x) - a+ 3 le 0`, where a is real parameter.
The given inequality has at least one negative solution for `a in ` (a) `(-oo,2)` (b) `(3,oo)` (c) `(-2,oo)` (d) `(2,3)`
View SolutionLet `a ,b ,c` be real. If `a x^2+b x+c=0` has two real roots `alphaa n dbeta,w h e r ealpha<-1a n dbeta>1` , then show that `1+c/a+|b/a|<0`
View SolutionIf `b gt a`, then the equation `(x-a)(x-b)-1=0` has
(a) Both roots in `(a, b)` `" "` (b) Both roots in `(-oo, a)`
(c) Both roots in `(b, +oo)` `" "` (d) One root in `(-oo, a)` and the other in `(b, +oo)`
View SolutionWhen `x gt -2`, find the values of `|x|` graphically.
View SolutionWhen `x lt 3`, find the values of `|x|` graphically.
View SolutionIf `2 le |x| le 5`, then find the values of x from the graph of `y = |x|`.
View SolutionDraw the graph of `f(x)= (|x-1|)/(x-1)`.
View SolutionDraw the graph of `x+ |y|=2y` and check the differentiability.
View SolutionDraw the graph of `f(x)= (x+2)|x-1|`.
View SolutionDraw the graph of the function `f(x)= x- |x-x^(2)|, -1 le x le 1` and find the points of non-differentiability.
View SolutionSolve : `x^(2)- |x+2|+x gt 0`
View SolutionDraw the graph of `f(x)= |2x-1|+ |2x-3|`. Find the range of the function.
View SolutionDraw the graph of `f(x)= |x|-|2x-3|`. Find the range of the function.
View SolutionLet `f(x)=x + 2|x+1|+2| x-1|`. Find the values of `k` if `f(x)=k`
(i) has exactly one real solution,
(ii) has two negative solutions,
(iii) has two solutions of opposite sign.
View Solution`f(x)=|a x-b|+c|x|AAx in (-oo,oo),` where `a >0, b >0,c > 0.` Find the condition if `f(x)` attains the minimum value only at one point.
View Solutionabout to only mathematics
View SolutionIf a continuous function `f` defined on the real line R assume positive and negative values in R, then the equation `f(x)=0` has a root in R. For example, if it is known that a continuous function `f` on R is positive at some point and its minimum value is negative, then the equation `f(x)=0` has a root in R. Consider `f(x)= ke^(x)-x`, for all real x where k is a real constant.
The positive value of k for which `ke^(x)-x=0` has only one root is
View SolutionIf a continuous function `f` defined on the real line R assume positive and negative values in R, then the equation `f(x)=0` has a root in R. For example, if it is known that a continuous function `f` on R is positive at some point and its minimum value is negative, then the equation `f(x)=0` has a root in R. Consider `f(x)= ke^(x)-x`, for all real x where k is a real constant.
For k > 0, the set of all values of k for which `y=ke^(x)-x=0`has two distinct roots is
View SolutionIf `x` and `y` are arbitrary extensive variables, then
View SolutionFind the number of solution of `2^x+3^x+4^x-5^x=0`
View SolutionDraw the graph of `y= log_(x)sqrtx`
View SolutionFind the number of roots of the equation `xlog_(e)x= 1`.
View SolutionIf the graphs of the functions`y= log _(e)x and y = ax` intersect at exactly two points,then find the value of `a`.
View Solutiondraw the graph of `f(x)=x+[x]`, [.] denotes greatest integer function.
View SolutionDraw the graph of the function `f(x) = x-|x2-x| -1 le x le 1`, where `[*]` denotes the greatest integer function. Find the points of discontinuity and non-differentiability.
View SolutionDraw the graph of `f(x) = [x^(2)], x in [0, 2)`, where `[*]` denotes the greatest integer function.
View SolutionDraw the graph of `f(x)= [sqrtx], x in [0, 16)`, where `[*]` denotes the greatest ineger function.
View SolutionDraw the graph of `y= [x]+ sqrt(x-[x])`, where`[*]` denotes the greatest ineger function.
View SolutionDraw the graph of `f(x) = [log_(e)x], e^(-2) lt x lt 10`, where `[*]` represents the greatest integer function.
View SolutionSolve `x^2-4x-[x]=0` (where `[]` denotes the greatest integer function).
View SolutionSketch the region of relation `[x] + [y] = 5, x, y ge 0`, where `[*]` denots the greatest integer function.
View SolutionDraw the graph of `f(x) ={2x}`, where `{*}` represents the fractional part function.
View SolutionFind the domain of `f(x) = sqrt (|x|-{x})` (where `{*}` denots the fractional part of x.
View SolutionSolve : `x^(2) = {x}`, where `{x}` represents the fractional part function.
View SolutionDraw the graph of `y^(2)= {x}`, where `{*}` represents the fractional part function.
View SolutionDraw the graph of `y =(1)/({x})`, where `{*}` denotes the fractional part function.
View SolutionSolve : `4{x}= x+ [x]`(where `[*]` denotes the greatest integer function and `{*}` denotes the fractional part function.
View SolutionGiven the graph of the function `y=f(x)`, draw the graph of `y ="sgn"(x)`.
View SolutionDraw the graph of `f(x) = "sgn"(x^(3) -x)`.
View SolutionDraw the graph of `f(x) = "sgn"(log _(e) x)`.
View SolutionLet a function `f(x)` be defined in `[-2, 2]` as
`f(x) = {{:({x}",",, -2 le xlt -1), (|"sgn "x|",",,-1le x le 1),({-x}",",, 1 lt xle 2):}` where `{x}` and sgn `x` denote fractional part and signum functions, respectively. Then find the area bounded by the graph of `f(x)` an the x-axis.
View SolutionLet `f: R to R ` be defined as `f(x) = e^("sgn "x)+ e^(x^(2))`. Then find the range of the function, and also indentify the type of the function : one-one or many-one.
View SolutionDraw the graph of the function `f(x) = "max"{x, x^(2)}` and write its equivalent definition.
View SolutionLet `f : R to R ` be a function defined by `f(x) = max. {x, x^(3)}`. The set of all points where `f(x) ` is NOT differenctiable is
(a) `{-1, 1}`
(b) `{-1, 0}`
(c ) `{0, 1}`
(d) ` {-1, 0, 1}`
View SolutionFind the equivalent definition of `f(x)=m a xdot{x^2,(-x)^2,2x(1-x)}w h r e0lt=xlt=1`
View SolutionLet f:` R to R and g:R to R` be respectively given by `f(x) =|x|+1 and g(x) =x^(2)+1)`. Define `h: R to R ` by
`h(x) ={{:( max{f(x) , g(x) },if xle0),(min{f(x) ,g(x) },if x gt 0):}`
then number of point at which h(x) is not differentiable is
View SolutionSketch the region of the points satisfying `max. {|x|, |y|} le 4`.
View SolutionConsider the regions `A={(x,y)|x^(2)+y^(2)le100} and B=|(x,y)|sin(x+y)gt0}` in the plane. Then the area of the region `AnnB` is
View SolutionDraw the graphs of the following parabolas :
(i) `x=y ^(2) - 2y -3`
(ii) `x = 6+y -y^(2)`
View SolutionFind the number of roots of the equation `e^(x) = sqrt (-x)`.
View SolutionLet `g(x)=sqrt(x-2k),AA2klt=x<2(k+1),` where `k in ` integer. Check whether `g(x)` is periodic or not.
View SolutionPlot the region in the first quadrant in which points are nearer to the origin than to the line `x=3.`
View SolutionDraw the graph of `y= sqrt (x^(2)-1)`
View SolutionDraw the graph of `y= -sqrt (6-3x^(2))`
View SolutionThe eccentricity of the ellipse `9x^2+25 y^2-18 x-100 y-116=0` is a.`25/16` b. `4/5` c. `16/25` d. `5/4`
View SolutionFind the area enclosed by the curves `y= sqrtx and x= -sqrty` and the circle `x^(2) + y^(2) =2` above the x-axis.
View SolutionConsider a square with vertices at `(1,1),(-1,1),(-1,-1),a n d(1,-1)dot` Set `S` be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region `S` and find its area.
View Solution
ILLUSTRATIONS questions and complete solutions for chapter GRAPHS OF ELEMENTARY FUNCTIONS of CENGAGE MATHS (ENGLISH) of Class 12