Complete Solutions to Illustration of chapter MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS |
| CENGAGE NEW | Illustration |
| Number Of Questions | 92 |
| Academic Year | 2023-24 |
Check the nature of the following differentiable functions (i) f(x) =`e^(x)`+sin xc,x in `R^(+)` (ii)f(x)=sinx+tan x-`2x,x in(0,pi//2)`
View SolutionProve that the function `f(x)=(log)_e(x^2+1)-e^(-x)+1` is strictly increasing `AAx in Rdot`
View SolutionFind the least value of `k` for which the function `x^2+k x+1` is an increasing function in the interval (1,2)
View SolutionFind the range of values of `a` if `f(x)=2e^x-a e^(-x)+(2a+1)x-3` is monotonically increasing for all values of `xdot`
View SolutionIf f(x) and g(x) are differentiable and increasing functions then which of the following functions alwasys increases?
View SolutionLet `g(x)=(f(x))^3-3(f(x))^2+4f(x)+5x+3sinx+4cosxAAx in Rdot` Then prove that `g` is increasing whenever is increasing.
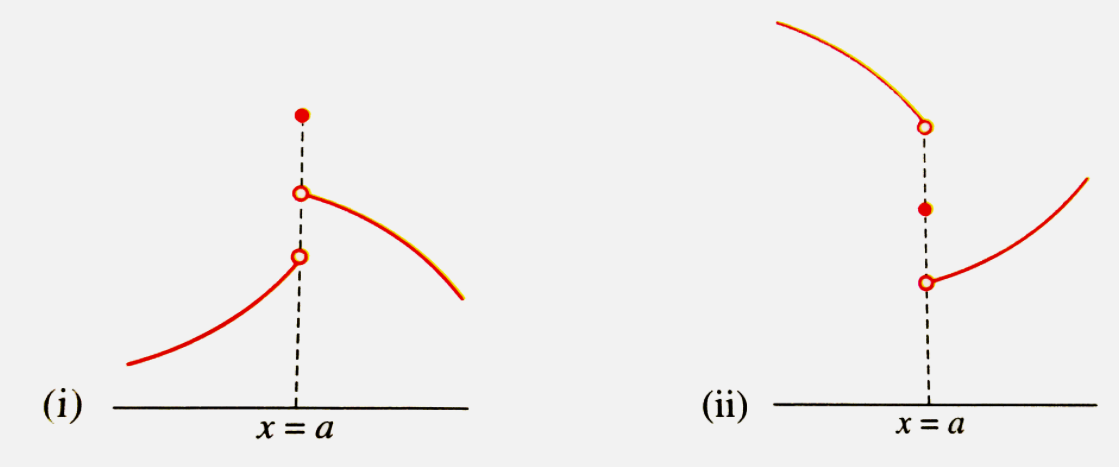
View SolutionFor each of the following graphs, comment whether f(x) is increasing or decreasing or neither increasing nor decreasing at x = a.
`
View SolutionFind the complete set of values of `alpha`for which the function
f(x) =`{(x+1,xlt1`
`alpha`, x =1 , is strictly increasing x=1
`x^(2)-x+3,xlt1`
View SolutionProve that function f(x) =`{-2x^(3)+3x^(2)-6x+5,xlt0` `-x^(2)-x+1, xge0` is decreasing for all x.
View SolutionIf `fogoh(x)` is an increasing function, then which of the following is not possible? `f(x),g(x),a n dh(x)` are increasing `f(x)a n dg(x)` are decreasing and `h(x)` is increasing `f(x),g(x),a n dh(x)` are decreasing
View SolutionLet `f(x)a n dg(x)` be two continuous functions defined from `RvecR` , such that `f(x_1)` > `f(x_2)` and `g(x_1)` < `g(x_2)` `for all` `x_1`>`x_2` `dot` Then what is the solution set of `f(g(alpha^2-2alpha)` > `f(g(3alpha-4))`
View SolutionLet `f:[0,oo)vec[0,oo)a n dg:[0,oo)vec[0,oo)` be non-increasing and non-decreasing functions, respectively, and `h(x)=g(f(x))dot` If `fa n dg` are differentiable for all points in their respective domains and `h(0)=0,` then show `h(x)` is always, identically zero.
View SolutionFind the values of `p` if `f(x)=cosx-2p x` is invertible.
View SolutionFind the critical points(s) and stationary points (s) of the function `f(x)=(x-2)^(2//3)(2x+1)`
View SolutionSeparate the intervals of monotonocity of the following function:
(i) `f(x)=3x^(4)-8x^(3)-6x^(2)+24x+7`
(ii) `F(x) =-sin^(3)x+3sin^(2)x+5,x "in" (-pi//2,pi//2)`
(iii) `f(x)=(2^(x)-1)(2^(x)-2)^(2)`
View Solutionअंतराल ज्ञात कीजिए जिन पर
`f(x) =(4 sin x - 2x - x cos x )/(2+ cos x)`
से प्रदत फलन f(i) निरंतर वर्धमान (ii) निरंतर ह्रासमान है |
View SolutionFind the interval of monotonocity of the function `f(x)=|x-1|x^2dot`
View SolutionFind the intervals of decrease and increase for the function `f(x)=cos(pi/x)`
View SolutionLet `g(x)=f(x)+f(1-x)` and `f''(x)>0AAx in (0,1)dot` Find the intervals of increase and decrease of `g(x)dot`
View SolutionFind the range of the function f(x) =x Si x-`(1)/(2) sin^(2)` x for xin `(0,(pi)/(2))`
View SolutionFind the range of f(x)=`(1)/(pi)sin^(-1)x+tan^(-1)+(x+1)/(x^(2)+2x+5)`
View SolutionFind the number of roots of the equation `log_(e)(1+x)-(tan^(-1)x)/(1+x)=0`
View SolutionFind the number of roots of the function `f(x)=1/((x+1)^3)-3x+sinxdot`
View SolutionProve that `log_(e)(1+x)ltxforxgt0`
View SolutionLet `fa n dg` be differentiable on `R` and suppose `f(0)=g(0)a n df^(prime)(x)lt=g^(prime)(x)` for all `xgeq0.` Then show that `f(x)lt=g(x)` for all `xgeq0.`
View SolutionShow that `1+xin(x+sqrt(x^2+1))geqsqrt(1+x^2)` for all `xgeq0.`
View SolutionIf `a , b >0a n d0
View SolutionProve that `|cosalpha-cosbeta|lt=|alpha-beta|`
View SolutionIf `P(1)=0a n d(d P(x))/(dx)>P(x)` for all x>=1. Prove that P(x)>0 for all x>1
View SolutionFor `0ltxlt(pi)/(2)`,prove that `x gt sin x `
View SolutionProve that `e^(x) ge 1 +x` and hence `e^(x) +sqrt(1+e^(2x))ge(1+x)+sqrt(2+2x+x^(2)) forall` x in R
View SolutionSeparate the intervals of concavity of the following functions
(i) f(x)=`sin^(-1)x`,(ii) f(x)=x+sinx
View SolutionIf graph of the function f(x) =`3x^(4)+2x^(3)+ax^(2)-x+2` is concave upward for all real x, then find values of a,
View SolutionProve that for any two numbers `x_(1) and x_(2)`
`(2e^(x)+e^(x))/(3)gte(2x_(1)+x_(2))/(3)`
View SolutionIf A+B+C=π Prove that in triangle ABC, sin `A+sin B+Cle(3sqrt(3))/(2)`
View SolutionProve that `a_(1)^(m)+a_(2)^(m)+….+a_(n)^(m)()/(n)lt(a_(1)+a_(2)+..+a_(n))/(n)^(m)`
If `0ltmlt1 and a_(i)gt0` for all I.
View SolutionFind the points of inflection for `f(x)=sinx` `f(x)=3x^4-4x^3` `f(x)=x^(1/3)`
View SolutionFind the coordinates of the point of inflection of the curve f(x) `=e^(-x^(2))
View SolutionThe function y=`(ax+b)/(x-1)(x-4)` has turning point at P(2,-1) Then find the values of a and b.
View SolutionHow many ciritcal points functionf(x)=(x-1)|x-3|-4x+12 has? How many of these are points of local extrema?
View SolutionDiscuss the extremum of the function f(x)=(x-1)(x-2)(x-3).How many criticla points f(x) has?
View SolutionFind the points of extrema of the function f(x)=2 sec x+3 cosec x
View SolutionProve that for all a,b in the function f(X) `=3x^(4)-4x^(3)+6x^(2)+ax+b` has exactly one extremium.
View SolutionThe function `f(x)=(x^2-4)^n(x^2-x+1),n in N ,` assumes a local minimum value at `x=2.` Then find the possible values of `n`
View SolutionTest f(x)={x} for the existence of alocal maximum and minimum at x=1, where{.} represents the fractional part function.
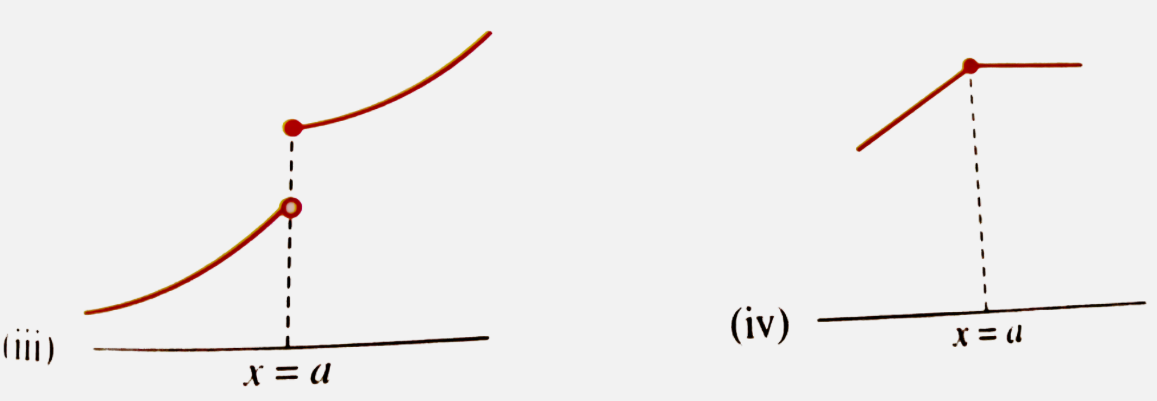
View SolutionConsider the following graphs of the functions. Check each for the extrema at x=a
View SolutionLet f(x)=`{x^(3)+x^(2)+10x, xlt0`.Investigate x=0 for local
`-3sinx,xge0`
maxima/minima.
View SolutionLet `f(x)=a/x+x^2dot` If it has a maximum at `x=-3,` then find the value of `adot`
View SolutionDiscuss the extremum of `f(x)=sinx(1+cosx),x in (0,pi/2)`
View SolutionFind the points at which the function `f` given by `f(x)=(x-2)^4(x+1)^3` has local maxima and local minima and points of inflexion.
View SolutionDiscuss the extremum of `f(x)=40(3x^4 + 8x^3-18 x^2+60)dot`
View SolutionDiscuss extrema of the function
`f(x) =int_(1)^(x)2(x-1)(x-2)^(3)+3(x-1)^(2)(x-2)^(2)dx`
View SolutionLet `f(x)=sin^3x+lambda sin^2x , -pi/2 < x < pi/2` Find the intervals in which `lambda` should lie in order that `f(x)` has exactly one minimum and exactly one maximum.
View SolutionLet `f(x)=sin^3x+lambda sin^2x , -pi/2 < x < pi/2` Find the intervals in which `lambda` should lie in order that `f(x)` has exactly one minimum and exactly one maximum.
View SolutionDiscuss the extrema of `f(x)=x/(1+xtanx),x in (0,pi/2)`
View SolutionDetermine which is bigger,`(1)/(pi)^(1/e) or (1)/(e )^((1)/(pi))`?
View SolutionDiscuss the extrema of the following functions
`(i)f(x)=|x|,(ii)f(x)=e^(-|x|),(iii) f(x)=x^(2//3)`
View SolutionIf 1`f(x)={x^(2),xle0`.Investigate the functions at x for maxima/manima
View SolutionDiscuss the extremum of `f(x)=2x+3x^(2/3)`
View Solution`f(x)={cos(pix)/2,x >0 x+a ,xlt=0` Find the values of `a` if `x=0` is a point of maxima.
View Solutionabout to only mathematics
View Solution`f(x)=|a x-b|+c|x|AAx in (-oo,oo),` where `a >0, b >0,c > 0.` Find the condition if `f(x)` attains the minimum value only at one point.
View SolutionLet `f(x)=2x^3-9x^2+12 x+6.` Discuss the global maxima and minima of `f(x)in[0,2]a n d(1,3)` and, hence, find the range of `f(x)` for corresponding intervals.
View SolutionFind the absolute maximum and absolute minimum values of `f(x)=3x^4-8x^3+12 x^2-48 x+25` in `[0,\ 3]`
View SolutionFind the range of the function `f(x)=4cos^(3)x-8cos(2)x+1`.
View SolutionFind the range of the function `f(x)=2sqrt(x-2)+sqrt(4-x)`
View SolutionA function y =f(x) is represented parametrically as following
`x=phi(t)=t^(5)-20t+7`
`y=psi(t)=4t^(3)-3t^(2)-18t+3`
where t in [-2,2]
Find the intervals of monotonicity and also find the points of extreama.Also find the range of function.
View SolutionFind how many roots of the equations `x^4+2x^2-8x+3=0.`
View SolutionDraw the graph of `y=x^(2)/sqrt(x+1)`
View SolutionDraw the graph of `y=xe^(x)`. Find the range of the function. Also find the point of inflection.
View SolutionMinimum integral value of k for which the equation `e^(x)=kx^(2)` has exactly three real distinct solution,
View SolutionDraw the graph of `f(x)=log_(e)(sqrt(1-x^(2)))`.Find the range of the function .Also find the values of k if f(x) has two distinct real roots.
View SolutionDraw the graph of `f(x)=(x^2-5x+6)/(x^2-x)`
View SolutionFind the value of `a` if `x^3-3x+a=0` has three distinct real roots.
View SolutionProve that there exist exactly two non-similar isosceles triangles `A B C` such that `tanA+tanB+tanC=100.`
View SolutionIf `t` is a real number satisfying the equation `2t^3-9t^2+30-a=0,` then find the values of the parameter `a` for which the equation `x+1/x=t` gives six real and distinct values of `x` .
View SolutionThe tangent to the parabola `y=x^2` has been drawn so that the abscissa `x_0` of the point of tangency belongs to the interval [1,2]. Find `x_0` for which the triangle bounded by the tangent, the axis of ordinates, and the straight line `y=x0 2` has the greatest area.
View SolutionFind the point `(alpha,)beta` on the ellipse `4x^2+3y^2=12 ,` in the first quadrant, so that the area enclosed by the lines `y=x ,y=beta,x=alpha` , and the x-axis is maximum.
View Solution`L L '` is the latus rectum of the parabola `y^2`= 4ax and PP' is a double ordinate drawn between the vertex and the latus rectum. Show that the area of the trapezium `P P^(prime)L L '` is maximum when the distance `P P '` from the vertex is `a//9.`
View SolutionFind the points on the curve `5x^2-8x y+5y^2=4` whose distance from the origin is maximum or minimum.
View SolutionRectangles are inscribed inside a semi-circle of radius `rdot` Find the rectangle with maximum area.
View SolutionA running track of 440 ft is to be laid out enclosing a football field, the shape of which is a rectangle with a semi-circle at each end. If the area of the rectangular portion is to be maximum, then find the length of its sides.
View SolutionIf the sum of the lengths of the hypotenuse and another side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between these sides is `pi/3dot`
View SolutionThe tangent to the parabola `y=x^2` has been drawn so that the abscissa `x_0` of the point of tangency belongs to the interval [1,2]. Find `x_0` for which the triangle bounded by the tangent, the axis of ordinates, and the straight line `y=x0 2` has the greatest area.
View SolutionFind the point `(alpha,)beta` on the ellipse `4x^2+3y^2=12 ,` in the first quadrant, so that the area enclosed by the lines `y=x ,y=beta,x=alpha` , and the x-axis is maximum.
View Solution`L L '` is the latus rectum of the parabola `y^2`= 4ax and PP' is a double ordinate drawn between the vertex and the latus rectum. Show that the area of the trapezium `P P^(prime)L L '` is maximum when the distance `P P '` from the vertex is `a//9.`
View SolutionFind the points on the curve `5x^2-8x y+5y^2=4` whose distance from the origin is maximum or minimum.
View SolutionA sheet of area `40m^2` is used to make an open tank with square base. Find the dimensions of the base such that the volume of this tank is maximum.
View SolutionA sheet of area `40m^2` is used to make an open tank with square base. Find the dimensions of the base such that the volume of this tank is maximum.
View SolutionThe lateral edge of a regular hexagonal pyramid is `1c mdot` If the volume is maximum, then find its height.
View SolutionShow that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius `R` is `(2R)/(sqrt(3))` .
View SolutionShow that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi vertical angle is one-third that of the cone and the greatest volume of cylinder is `4/(27)pih^3tan^2alphadot`
View Solution
Illustration questions and complete solutions for chapter MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS of CENGAGE MATHS (ENGLISH) of Class 12
All Exercises from CENGAGE NEW Class 12 MATHS MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- Concept Application Exercise 6.1
- Concept Application Exercise 6.2
- Concept Application Exercise 6.3
- Concept Application Exercise 6.4
- Concept Application Exercise 6.5
- Concept Application Exercise 6.6
- Concept Application Exercise 6.7
- Exercise
- Illustration
- Linked comprehension type
- Linked comprehension Type
- Matrix Match Type
- Multiple correct answers type
- Numerical Value Type
- Single Correct Answer Type
- Solved Examples