Complete Solutions to SOLVED EXAMPLES of chapter CURRENT ELECTRICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CURRENT ELECTRICITY |
| MODERN PUBLICATION | SOLVED EXAMPLES |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
If current in a conductor linearly drops to zero from initial magnitude `i_0` in time interval `t_0` what amount of charge must have passed through the conductor ?
View SolutionThe frequency of revolution of electrons of electron in its orbit arount some nucleus is `3xx10^(15)` revolutions per seconds .
If we consider the motion of electron as one loop of current , what should be the magnitude of equivalent electric current ?
View SolutionThe speed of electron in a circular orbit of `0.5 Å`, around the proton in a hydrogen atom is `2xx10^6` m/s.
Calculate the equivalent currrent assuming motion of electron as one current loop.
View SolutionThe variation of current for an interval of 20 seconds is shown in the graph. Calculate the amount of charge that must have flown in this interval of time

View SolutionIf a charge flowing through a cross section of wire can be written as `q=5t^2+8tC`, then calculate the electric current at t=0 and t=2s. Calculate the amount of charge that must have flown in the interval of 2 seconds starting from t=0 and also calculate the average electric current for this interval.
View SolutionAssume two copper rods A and B are connected to each other at one end. Lengths of the rods ar equal.
Radii of cross section of A and B are 2 mm and 4 mm respectively. If the current density in A is `9xx10^5 A//m^2` then calculate the current density in B.
View SolutionIf one mole of electrons is passing from point P to another point Q on a straight metal wire in time interval of 1 ms, then what will be the magnitude of current in the wire ? What is the direction of current ?
View SolutionHow many electrons should flow per seconds to constitute a current of magnitude one ampere ?
View SolutionAn incandescent lamp draws a current of 0.5 ampere.
How many electrons are passing through the filament of lamp every hour ?
View SolutionWe know that copper is a conductor of electricity due to presence of free electrons in it. Assume that on an average each copper atom provides one free electron. Find the number of free electrons per unit valume of copper. The density of copper is approximately 9,000 kg /`m^3` and its atomic mass is 63.5 u.
View SolutionThere is a copper wire of radius 1mm and it carries a current of 2 ampere, calculate the drift speed of electrons assuming there are `8.5 xx10^(28)` free electrons per metre cube.
View SolutionA copper wire of cross sectional area `0.5 mm^2` carries a currents of 1A . Assume that each copper atom contributes one free electron . The density of copper is 9,000 `kg//m^3` and atomic mass is 63.5 u. if `v_d` is drift speed of electrons. Now assume that one copper atom is kept at temperature 300 K and it develops thermal motion. Let `v_("rms")` be the root mean square speed of copper atom at given temperature . find the ratio `v_(rms)//v_d` ( HInt: Treat copper atom like a mono-atomic gas particle for the calculation of `v_(rms)`)
View SolutionA metallic wire A of radius 1 mm is joined at one end with another metallic wire B of radius 2 mm .
when a battery is connected between two free ends of this composite wire, a currents of 20 A flows through it.
Calculate the currents density in wire A and also calculate the drift speed of electrons in wire B , if material of B has `9xx 10^(29)` free electrons per unit volume.
View SolutionThe mobility of electrons is defined as the drift velocity acquird by electrons when a unit electric field is applied.
Let a potential diffrence of 120 V be applied across a straight conductor of length 1m. What will be the drift speed of electrons if the mobility of electrons is given to be `6xx10^(-6)m^2V^(-1)s^(-1)` ?
View SolutionThere is a conducting wire of length l and radius of cross section r. The number of free electrons per unit volume of the conductor is n and the mobility of electrons is `mu`. A battery of potential difference V is connected across its length. Find electric current flowing through the wire. Assume e as the magnitude of charge on electron.
View SolutionThere is one rod of metal whose electrical resistance is R. What will be the new resistance if the rod is stretched to
(a) double its initial length?
(b) increase its length by double of its initial length ?
Assume that density of material remains constant.
View SolutionThere is one hollow pipe of metal of length L . The inner radius of the pipe is `r_1` and the outer radius is `r_2` . The resistivity of material of pipe is `rho`. Find the resistance.
View SolutionA thin copper rod of radius 1mm having an electrical resistance of `100 Omega` is connected to battery of emf 12 volts and negligible internal resistance through a wire of negligible resistance. Calculate current density in the wire. Also , calculate the number of electrons entering one and of the rod per seconds.
View SolutionThe resistivity of copper is approximately `1.67xx10^(-8)Omegam`.
Calculate the electrical resistance of a hollow tube made of copper of external radius 20 cm and length 20 cm . The thickness of copper is 50 mm .
View SolutionThe current density in a conductor is `5 A //m^2` when an electric field of 50 V/m is applied across it. Calculate the conductivity of the material.
View SolutionThe electrical resistance of a 5 m long wire is `3 Omega` Calculate the electrical resistivity and conductivity of material if its cross section is `0.03 mm^2` .
View SolutionWe have a 100 m long thin copper wire of resistance `100 Omega` it is melted to make a small rod of length 10 m.
what will be the new resistance ?
View SolutionWe have one wire of resistance `R_1` and it is stretched to n times its initial length to change its resistance to `R_2` calculate `R_2//R_1` .
View SolutionTwo cylinders P and Q of equal mass are made from the same metal. If the radius of P is n times the radius of Q , then calculate ratio of their resistances.
View SolutionA wire made of material A has resistance `R_1` another wire made of material B having P time the length and q times the radius of first wire has resistance `R_2` . If resistivity of B is r times that of A, then calculate`R_2//R_1` .
View SolutionCurrent flowing in two wires A and B of the same length is same when the same potential difference is applied across them. If conductivity of A is n times to that of B, then calculate the ratio of radii of cross section of the two wires.
View SolutionCalculate the drift speed developed in a metal wire when V potential difference is applied across length l of the wire. The number of free electrons per unit volume is n and conductivity of the material is `sigma`.
View SolutionThe resistivity of material of a wire is `2xx10^(-8) Omegam` and the number of free electrons per unit volume is `9xx10^(28)` per `m^3` . Calculate the relaxation time which is defined as the average time interval between two successive collisions.
Also calculate the mean free path of electron (distance covered by electron between two successive collisions) if the drift velocity of electrons is `1.7 xx10^(-4)m//s`.
View SolutionThe density of silver is 10.5 g/cc and its atomic mass is approximately 108 g . Assume each atom contributes one free electron and calcute the number of free electrons per unit volume for the silver. Resistivity of the silver is `1.6 xx10^(-8) Omega`m.
What potential difference must be applied across the silver wire of length 0.1 m and area of cross section `1mm^2` so that a current of 2A flows through it ? what will be the current density for the wire and drift speed of electrons ?
View SolutionUsing the microscopic form of Ohm's law `(J=sigma E)` , prove that conductivity of a metal can be written as `sigma="ne"mu`. Here n is the number of free electrons per unit volume and `mu` is mobility of free electrons . In case of semiconductors there are two types of conduction particles, one is free electrons and the other is known as a hole. Charge on the hole may be assumed to be equal and opposite of that on electron. The number density of free electrons and holes in the semiconducting material are n and p respectively. Assuming `mu_e and mu_h` as mobility of free electrons and holes respectively , write the exopression of conductivity of the semiconducting material.
View SolutionThe temperature coefficient of resistance of a material is `0.004 ""^@C^(-1)`. Let `R_0` be the resistance of a wire made from this material at `0^@C` . What should be the temperature of this object so that its resistance increases by `2R_0` ?
View SolutionThe resistance of a thin metallic cylinder changes from `4.25 Omega "to" 4.75 Omega` when its temperture is incrased from `10^@C "to 110^@C`. Calculate the resistance of the same object when it is kept at temperature `0^@C` . Also calculate the temperature coefficient of resistance.
View SolutionThe temperature coefficient of resistance of tungsten is `0.0045^@C^(-1)`. A standard resistance made from this material is rated to have resistance `2 Omega` but it is found that resistance is `2.115 Omega` when measured at `40^@C`. If we assume that the difference is due to unknown temperature at which resistance rating is done, then calculate this temperature.
View SolutionCalculate the effective resistance between A and B in the given circuit. All resistances shown are R.

View SolutionThere is one rod of length L. the resistivity of its material is given by `rho=alphax+beta`. Here x is the distance of `alpha` point on rod from one of its ends. Assume A as the area of cross section of rod. Find the electrical resistance of the rod.
View SolutionA metallic wire with resistance `lambda` per unit length is bent to form `alpha` circle of radius R. Calculate the effective resistance between the effective resistance between the points P and Q , making an angle of `90^@` with each other at the centre.

View SolutionCalculate the current drawn from the battery in the following circuit.

View SolutionCalculate the equivalent resistance between A and B in the following network.

View SolutionTwo resistance `R_1 and R_2` when connected in series produce equivalent resistance equal to x. and when the same two resistance are connected in parallel then equivalent resistance becomes y. Calculate the product of magnitudes of `R_1 and R_2` in terms of x and y.
View SolutionTwo resistors of 5 `Omega and 10 Omega` are connected in parallel to a battery of emf 16 V and a current of 4 A is drawn from the battery . How will you explain the given magnitude of current ? Do you see any discrepancy in the given magnitude of current ?
View SolutionTwo identical rectangular `(l xx b)` metal plates P and Q of same thickness are connected in series as shown in the figure and `alpha` current I is passed through the combination.

Let `V_P and V_Q` be the potential difference developed across both the plates. find `V_P//V_Q`. The material is same for both the plantes.
View SolutionWe have a wire of uniform cross section and its electrical resistance is R . This wire is cut in n equal parts and each part is stretched so that its length becomes equal to the length of the original wire. Now all these parts are connected in parallel. Calculate the equivalent resistance now.
View SolutionFind the equivalent resistance between A and B .

View SolutionA capacitor of `10 muF` is connected between the points P and Q of the following circuit. Calculate energy stored by the capacitor in steady state condition.

View SolutionFind eqvivalenet resistance between points P and Q for the following network of resistances.

View SolutionAll resistors are having same resistance R. Find the equivalent resistance between points A and D.

View SolutionFind the equivalent resistance between P and Q for the following network of circuit. All resistacnes are identical having the same resistance R

View SolutionCalculate the electric current drawn from battery in the given circuit.

View SolutionThree colour strips of a colour -coded resistor in order are blue, orange green. What current will flow through it when a battery of 100 volt is connected across it ?
View SolutionA battery of negligile internal resistance connected in a circuit is maintaining a current of 5 A and it is found that battery does a work of 800 J in an interval of 2 minutes. What is the emf of the battery ?
View SolutionPotential difference across the terminal of `alpha` battery drops by 1 V when `alpha` current of 1 A is drawn from its positive terminal by connecting it to `alpha` circuit . What is the internal resistacne of the battery ?
View SolutionA battery of unknown emf and internal resistance is given to a student for the experiment. When student connects the battery to an external resistance of `10 Omega` then 1A current flows through the circuit and when the same is connected to `15 Omega` resistance then 0.75 A current flows through the circuit . Calculate the emf and internal resistance of the given battery.
View SolutionWe have a chargeable battery of emf 12 V and internal resistance of `1 Omega` The battery can take a maximum of 20 A current during the charging process. If we have a charger, which can maintain a potential difference of 60 V, then what resistance is needed to be connected in series with the charger to charge the given battery ?
what terminal potential difference do you expect across the terminal of battery being charged ?
View SolutionThe terminal potential difference (V) between the terminals of a battery depends on current (i) according to the following relation.
`V=8-3i`
What is the emf of the battery ? What is the internal resistance of battery ?
View SolutionCalculate heat produced in five minutes across a resistor of `20 Omega` when 3A current flows through it .
View SolutionThe rating of an electric bulb is 220 V-100 W. if a rated voltage is applied then how many electrons will pass through the filament in one second ?
View SolutionAn electric iron is rated as 220 V-850W. What is the resistance of its heating element ? How much current will it draw when the rated voltage is applied on it ?
View SolutionThe efficiency of a motor is defined as the ratio of mechanical power output to that with input electric power. The motor is designed to operate at 100 V and it draws a current of 15 A . If output mechanical power of motor is 800 W, then calculate the efficiency of motor .
View SolutionThe rating of a heating element is 220 V-1,000 W. if the heating elements is stretched to double of its initial length then what will be the power rating for the same voltage ?
View SolutionThe stamp on an electic bulb reads 220V-60 W. if the supply voltage available is 100 V then what current will be drawn by the bulb ?
View SolutionTwo bulbs are rated as 220 V-100W and 220 V-60 W. How much power will be consumed when both of them are connected in series across the supply of 220 V ?
View SolutionOne heater coil takes time `t_1` to heat a glass of water and another takes time `t_2` to heat the same amount of water. How much time will it take to heat the same amount of water when the two are connected in series and when the two are connected in parallel ? voltage applied is same in all cases.
View SolutionState the characterisitics of fuse wire.
View SolutionIf a fuse wire of certain material blows at 10 A current, then what should be the radius of the fuse wire made from same material which blows at 20 A ?
View SolutionFind the potential difference across each cell and the rate of energy dissipated in R in the given figure .

View SolutionThe circuit diagram in figure below has two cells `varepsilon_1 and varepsilon_2` with emfs 4 V and 2V respectively, each one having an internal resistance of `2 Omega` The external resistance R is of `8 Omega` Find the magnitude and direction of currents flowing through the two cells .

View SolutionApply Kirchhoff's rules to the loops ACBPA and ACBQA to write the expressions for the currents `I_1,I_2 and I_3` in the network shown in the figure below.

View SolutionIn the network of resistors , connected to a battery of negligible internal resistance, find the equivalent resistance between the points A and B . If 1 A current is drawn from battery then what is the emf of battery ?

View SolutionCalculate the current flowing through each of the cells shown in the circuit below. Also calculate the potential difference across each cell.

View SolutionFor the circuit shown here Calculate the potential difference between B and D

View SolutionDetermine the currents flowing through the galvanometer G of the Wheatstone bridge as shown in the figure below, in the unbalanced position of bridge.

View SolutionFind the equivalent resistance between the terminals A and B in the network shown below Given the value of each resistance R is of `5 Omega` Also, calculate the current in the arm CF.

View SolutionBattery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance `1 Omega` (Fig. 3.23). Determine the equivalent resistance of the network and the current along each edge of the cube.
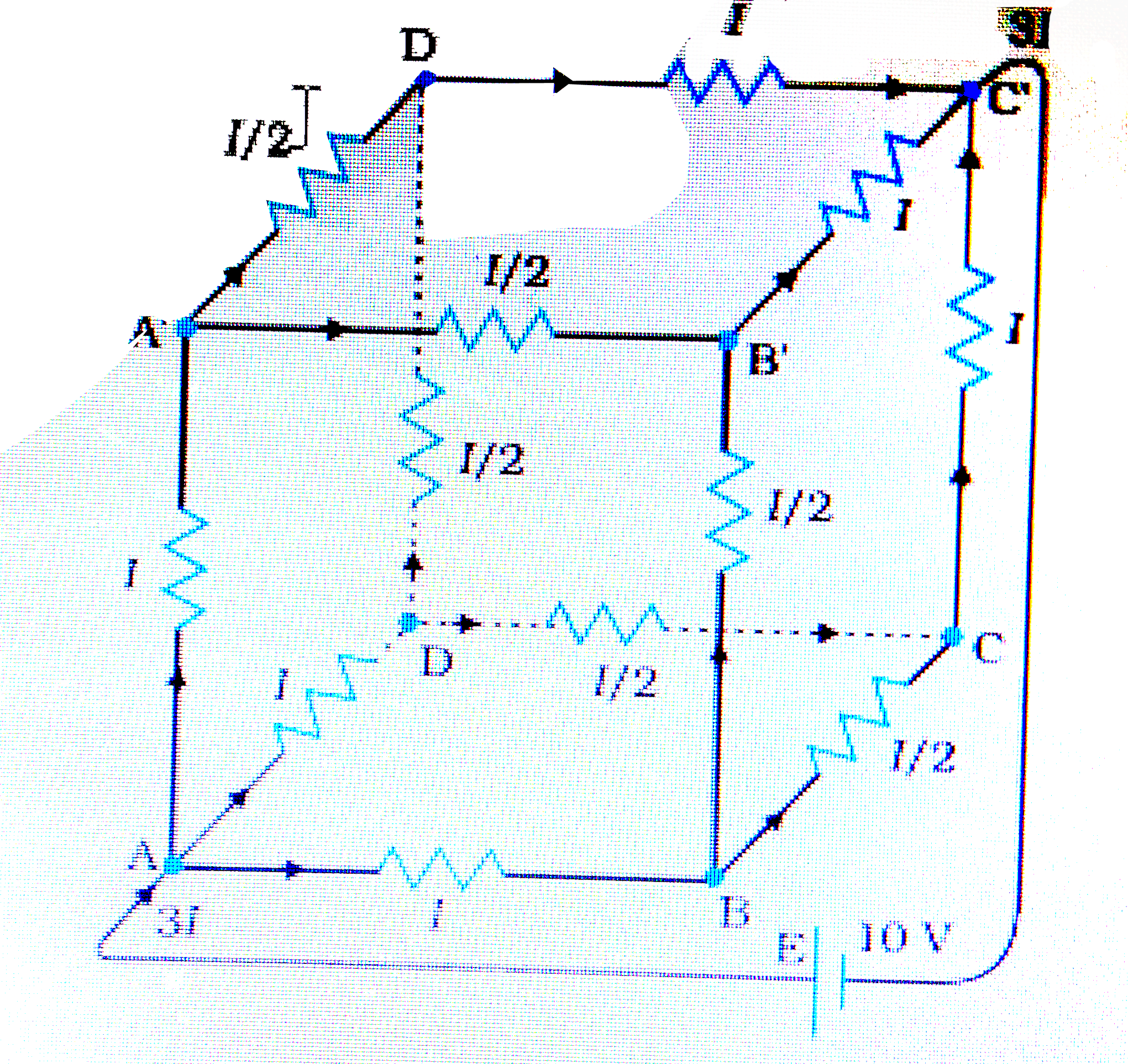
View SolutionFind the current supplied by battery of 12 V in the following circuit diagram . What is the potential difference across the `10 Omega` resistor ?

View SolutionFind the electric current drawn from a battery of emf 12 V for the following circuit. Consider the capacitor to by fully charged.

View SolutionCalculate `I,i_1,i_2 and i_3` for the following circuit.

View SolutionTwo batteries of emfs `E_1 and E_2` are connected to drive current in external resistance R , as shown in the given figure. The internal resistances are `r_1 and r_2` respectively .
Calculate the electric current flowing through external resistance R , and then evaluate the emf and internal resistance of one single battery that can replace the two used in circuit .

View SolutionA battery is formed by connecting three cells in series .
The emfs of cells are 5 V, 2.5 V and 1.5 V and their internal resistance are `0.5 Omega ,0.05 Omega and 0.45 Omega` respectively.
This battery is connected across a load resistance of `5 Omega` what current will be supplied by the battery ? if the cell of emf 1.5 V were connected with reverse polarity then what would have been the current supplied by the battery ?
View SolutionA resistance of `1 Omega` is connected to a battery of emf 2 V and internal resistance `0.4 Omega` what current is flowing through the circuit ? If another battery of double the emf is connected in series with the earlier one then current flowing in the circuit becomes double . what should be the internal resistance of battery ?
View SolutionA resistance of `97 Omega` is connected to a battery of emf 10 V . To measure the current passing in the circuit, an ammeter is inserted in series with the resistance. It is found that the ammeter reads 100 mA. What is the internal resistance of the battery if `2 Omega` is the resistance of ammeter ?
View SolutionHow can we convert a galvanometer into an ammeter ?
View SolutionThe wheatstone bridge shown in the given figure shows no deflection in the galvanometer joined between the point Q and S. calculate the values of X.

View SolutionCalculate the current drawn from the battery by the network of resistors shown in the figure.

View SolutionAll resistors in the following network are identical and having a resistacne R . Find the equivalent resistance between A and B as shown.

View SolutionFind the current drawn from the battery in the following circuit.

View SolutionEach resistor in the circuit has a resistance of `10 Omega` what currents is flowing through the battery ?

View SolutionFind the value of the unknown resistance X, in the following circuit, if no current flows through the section PO. Also calculate the current drawn by the circuit from the battery of emf 5V and negligible internal resistance .

View SolutionFind the equivalent resistance between the points A and B of the network shown in the figure given below.

View SolutionIn a metre bridge experimental set-up, shown in the figure below, the null point D is obtained at a distance of 40 cm from end A of the metre bridge wire. If a resistance of `10 Omega` is connected in series with X, null point is obtained at AD= 60 cm . Caluclate the values of X and Y.

View SolutionAn unknown resistance is connected in a left gap of a metre bridge . The balance point is obtained when a resistance of `10 Omega` is taken out from the resistance box in the right gap. On increasing the resistance from the resistance box by `12.5 Omega` the balance point shifts by 20 cm.
find the unknown resistance.
View SolutionA resistance `R=2 Omega` is connected to one of the gaps in a metre bridge ,which uses a wire of length 1m. An unknown resistance `X gt 2 Omega` is connected in the other gap as shown in the figure. The balance point is noticed at l from the positive end of the battery. on interchanging R and X, it is found that the balancing point further shifts by 20 cm (away from end A). Neglecting the end correction, calculate the value of unknown resistance X used

View SolutionAn ideal voltmeter and ammeter are connected in a circuit as shown in the figure. When the key is open, the voltmeter reads 24 V and when it is closed then the ammeter reads 0.5 Amp.

Calculate emf and internal resistance of the battery.
View SolutionA galvanometer shows full scale deflection when a current of 1 mA is passed through it . The resistance of the coil used in galvanometer is `100 Omega` How will you convert it into an ammeter which should be able to measure the current up to 5 A ?
View SolutionA galvanometer shows full-scale deflection when current of 1 mA is passed through it. Resistance of the coil used in the galvanometer is `100 Omega` what maximum potential difference can be measured if it is used as a voltmeter ? How will you modify it to measure potential difference up to 2 V ?
View SolutionA galvanomter scale is divided into 100 equal divisions. The current sensitivity is 10 divisions per mA and voltage sensitivity is 5 divisions per mV. How will you convert it to read (i) 8 A for full scale and (ii) 1 division per volt ?
View SolutionA 10 m long potentiometery wire has a resistance of `20 Omega` it is connected to a battery of emf 6 V and internal resistance `4 Omega` find the potential gradient along the wire.
View SolutionA constant voltage of 3 V is supplied to a potentiometer wire. A cell of emf 2 V is balanced by a voltage drop across 416 cm of the wire. Find the total length of the potentiometer wire.
View SolutionCalculate the current through branch EF in the circuit shown below.

View SolutionWhy are we getting zero current in the branch EF of the previous example ?
View SolutionIn figure given a long uniform potentiometer wire AB is having a constant potential gradient along its length. The null points for the two primary cells of emfs `varepsilon_1 and varepsilon_2` are connected in the manner shown are obtained at a distance of 120 cm and 300 cm from the end A. Find (i) `varepsilon_1//varepsilon_2` and (ii) position of null point for the cell `varepsilon_1`.
How is the sensitivity of potentiometer increased ?

View Solution
SOLVED EXAMPLES questions and complete solutions for chapter CURRENT ELECTRICITY of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 PHYSICS CURRENT ELECTRICITY
- Chapter Practice Test
- CONCEPTUAL QUESTIONS
- HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL
- NCERT SOLVED (NCERT Additional Exercises)
- NCERT SOLVED (NCERT Exemplar Problems Subjective Questions)(Short Answers Type Questions)
- NCERT SOLVED (NCERT Exemplar Problems Subjective Questions)(Very Short Answers Type Questions)
- NCERT SOLVED (NCERT Textbook Exercises)
- Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (A. MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER)
- Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION FOR COMPETITIVE EXAMINATIONS)
- Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION JEE (ADVANCED) FOR IIT ENTRANCE)
- Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION JEE (MAIN) & OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)
- Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (C. MULTIPLE CHOICE QUESTIONS WITH MORE THAN ONE CORRECT ANSWER)
- Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS ASSERTION REASON TYPE QUESTIONS)
- Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS BASED ON A GIVEN PASSAGE/COMPREHENSION)
- Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS INTEGER TYPE QUESTIONS)
- Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS MATRIX MATCH TYPE QUESTIONS)
- Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (NCERT EXEMPLAR PROBLEMS)
- PRACTICE PROBLEMS
- REVISION EXERCISES (ADDITIONAL QUESTIONS)
- REVISION EXERCISES (FILL IN THE BLANKS)
- REVISION EXERCISES (LONG ANSWER QUESTIONS)
- REVISION EXERCISES (NUMERICAL PROBLEMS)
- REVISION EXERCISES (SHORT ANSWER QUESTIONS)
- REVISION EXERCISES (VERY SHORT ANSWER QUESTIONS)
- SOLVED EXAMPLES
- TOUGH AND TRICKY PROBLEMS