Complete Solutions to Exercise 7a of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| NAGEEN PRAKASHAN | Exercise 7a |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
Which of the following pairs of triangles are congruent ? Also state the condition of congruency in each case :

(iv) In `DeltaABC` and `DeltaDEF, AB=EF, BC=DF` and `angleB=angleF`
(v) In `DeltaABC` and `DeltaPQR, AB=QR, AC=PR` and `angleB=angleR`
(vi) In `DeltaABC` and `DeltaPQR, angleA=angleP, AC=PR` and `AB=PQ`
(vi) In `DeltaABC` and `DeltaPQR, AB=QR, angle A=angle Q` and `AC=QP`.
View SolutionIn a `DeltaABC, D` in mid-point of BC, AD is produced upto E so that `DE=AD`, prove that :
(i) `DeltaABD` and `DeltaECD` are congruent (ii) `AB=EC`
(iii) AB is parallel to EC.
View SolutionIn the given figure, `AB=DB` and `AC=DC`. If `angleABD=58^(@), DeltaDBC=2x-4^(@), angleACB=y+15^(@)` and `angleDCB=63^(@)` find the values of `x` and `y.`

View SolutionBD is the disector of angle ABC. From a point P in BD, perpendiculars PE and PF are drawn to AB and BC respectively, prove that :
(i) Triangle BEP is conguent to triangle BFP (ii) PE=PF.
View SolutionGiven a `DeltaABD` in which `AB=AD` and `AC` bisects `BD`. Prove that :
`DeltaABC cong DeltaADC`.
View SolutionIn a tringle ABC, AB = AC and bisector of angle A meets BC at D. Prove that :
(i) `DeltaABD cong DeltaACD` (ii) `AD` is perpendicular to BC.
View SolutionIn quadrilateral ABCD, AB=DC and AD=BC. Prove that the sides AB and DC are parallel to each other.
View SolutionIn `DeltaABC, AB = AC` and the bisectors of `angleB` and `angleC` meet AC and AB at point D and E respectively. Prove that `BD = CE`.
View SolutionIn `DeltaABC, angleB= angleC`. Prove the perpendiculars from the mid-point of BC and AC are equal.
View SolutionFind the value of x and y in each of the following figures containing two congruent triangles :

View SolutionIn the adjoining figure, `angleBAC=angleBDC` and `angleABC=angleBCD`. Prove that :
(i) `DeltaABC cong DeltaDCB`
(ii) `DeltaABE cong DeltaDCF`.

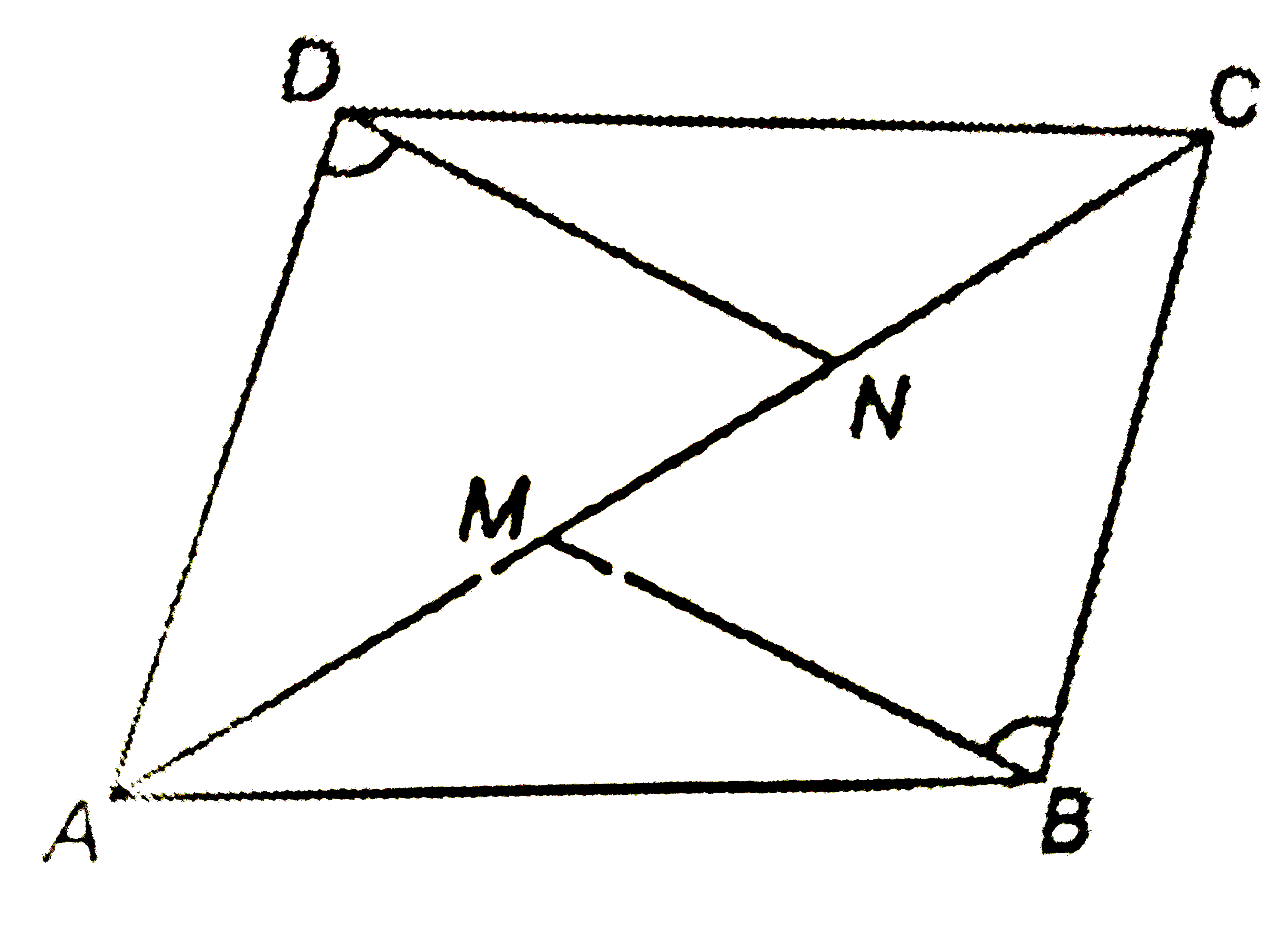
View SolutionIn the adjoining figure, ABCD is a quadrilateral. M and N are the points on AD and CD respectively such that `AB = BC, angleABM=angleCBN` and `angleMBD=angleNBD`. Prove that `BM = BN`.

View SolutionGiven `AD=DC` and DB biscets `angleADC`.
(i) Prove that, `DeltaADB cong DeltaCDB`
(ii) If `angleABD=48^(@)`, find `angleCBD`.
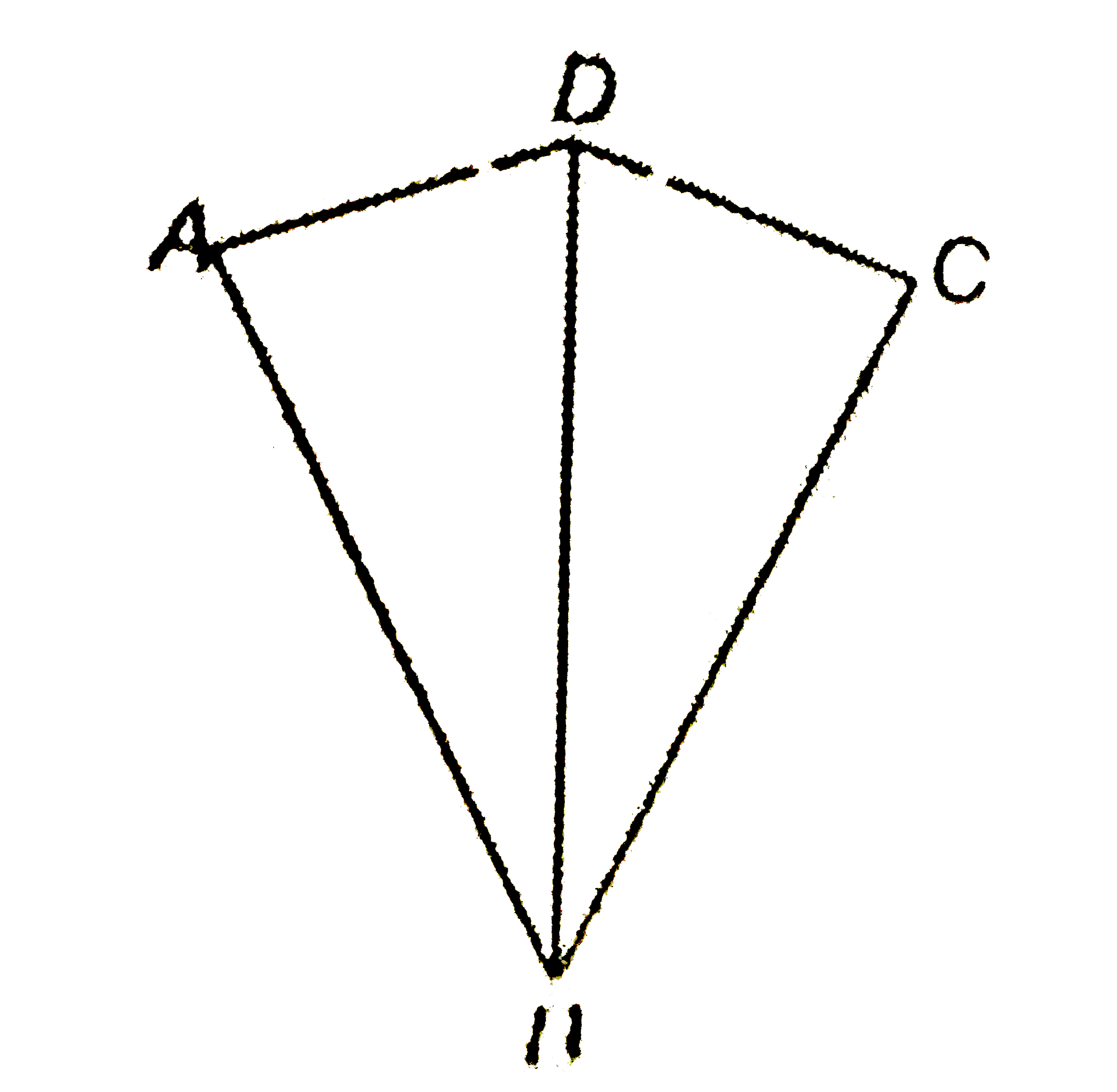
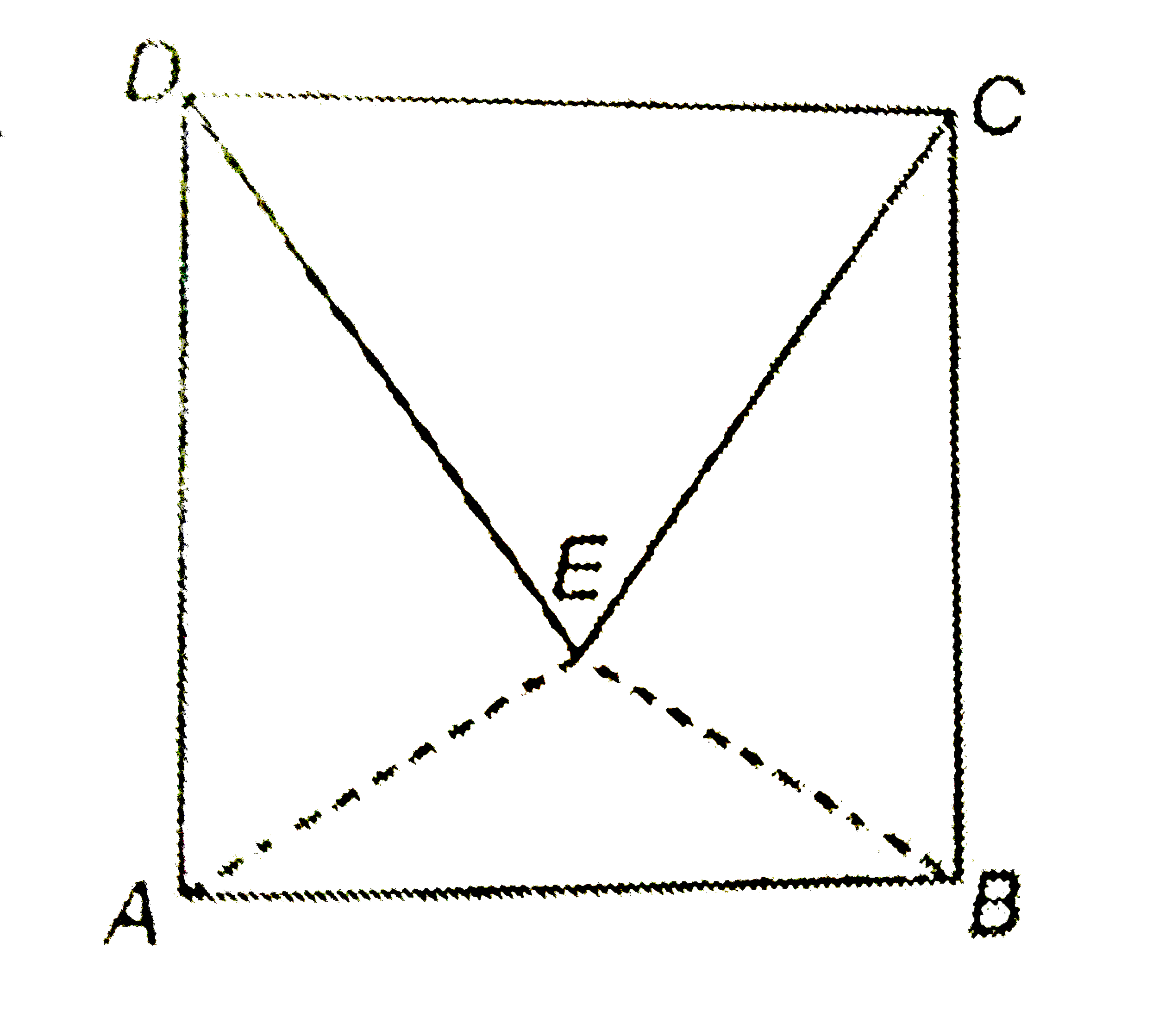
View SolutionThe adjoining figure shows a square ABCD and an equilateral triangle DEC. Prove that :
(i) `angleADE=angleBCE=30^(@)`
(ii) `Delta cong DeltaBCE`
View SolutionEquilateral triangles ABD and ACE are drawn on sides AB and AC respectively of a `DeltaABC` outside it. Prove that :
(i) `angleDAC= angleEAB` (ii) `DC = BE`
View SolutionThe following figure shows a square ABCD and an equilateral triangle DCE. Prove that :
(i) `angleADE=angleBCE=150^(@)`
(ii) `DeltaADE cong DeltaBCE`
(iii) `AE = BE`

View SolutionThe given figure showns a parallelogram ABCD. Squares ABPQ and ADRS are drawn on sides AB and AD respectively of the parallelogram ABCD. Prove that :
(i) `angleSAQ=angleABC`
(ii) `SQ=AC`
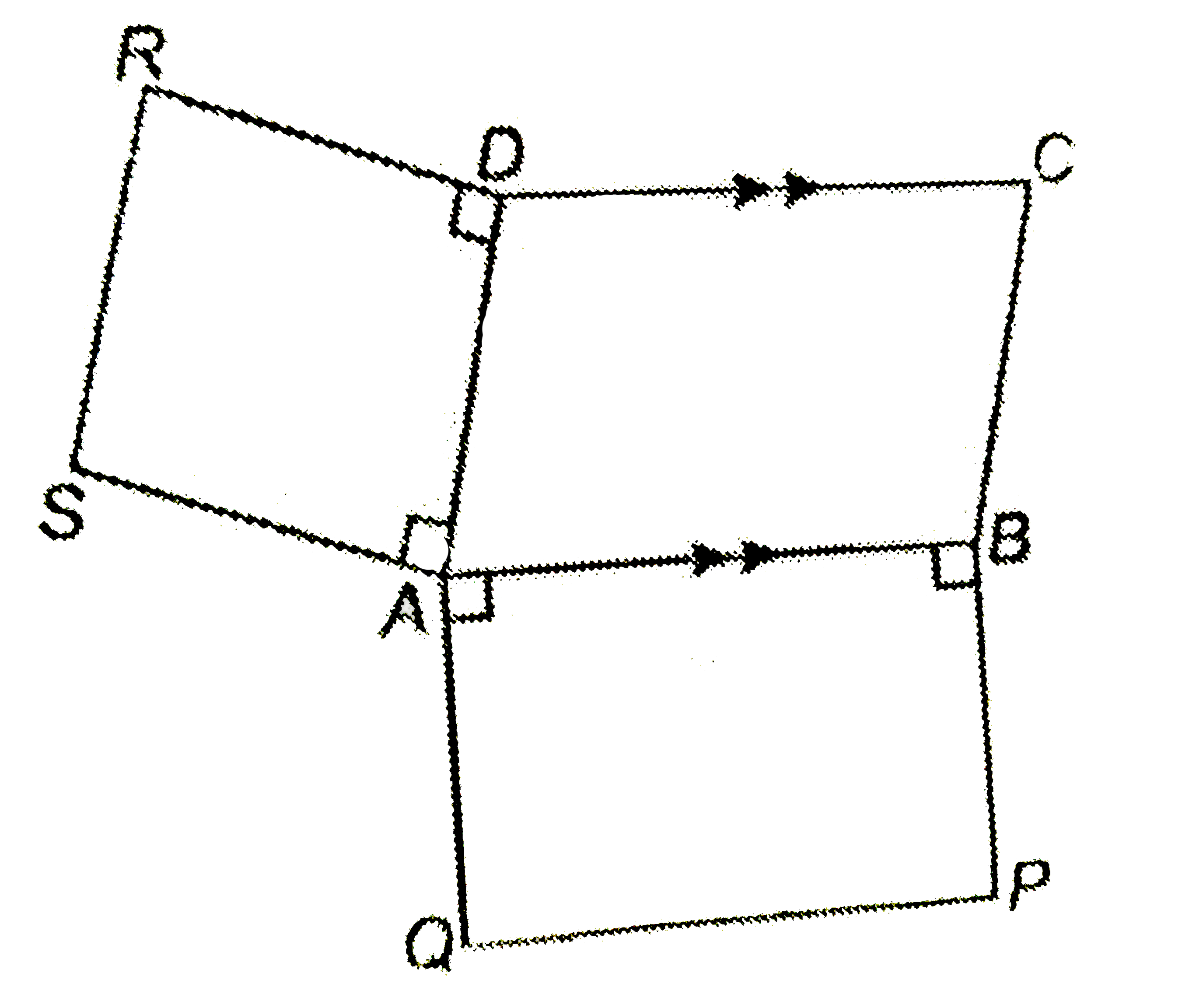
View SolutionIn a `DeltaABC, BD` is the median to the side Ac, BD is produced to E such that BD = DE. Prove that AE is parallel to BC.
View SolutionIn the given figure, `angleBDC=angleBEA` and `AB = BC`. Show that AE=CD.
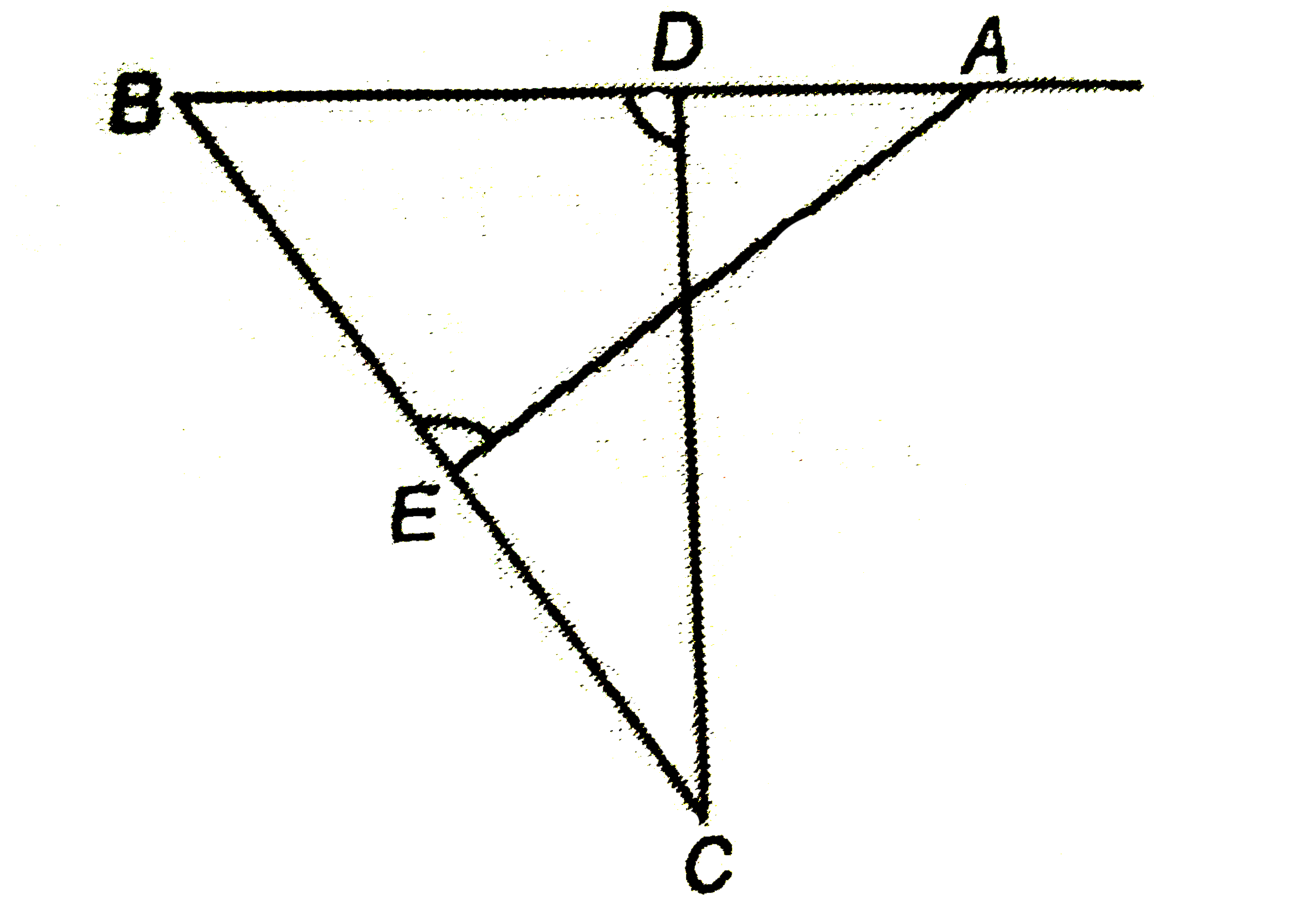
View SolutionIf the diagonals of a quadrilateral bisect each other at right angle, prove that the quadrilateral is a rhombus.
View SolutionIn the adjoining figure, BM and DN are the perpendiculars from B and D respectively to AC such that BM = DN. Prove that BO = OD.

View SolutionIn the adjoining figure, `AB=EF, BC=DE, angleABC=angleFED=90^(@)`, prove that `AD = CF`.
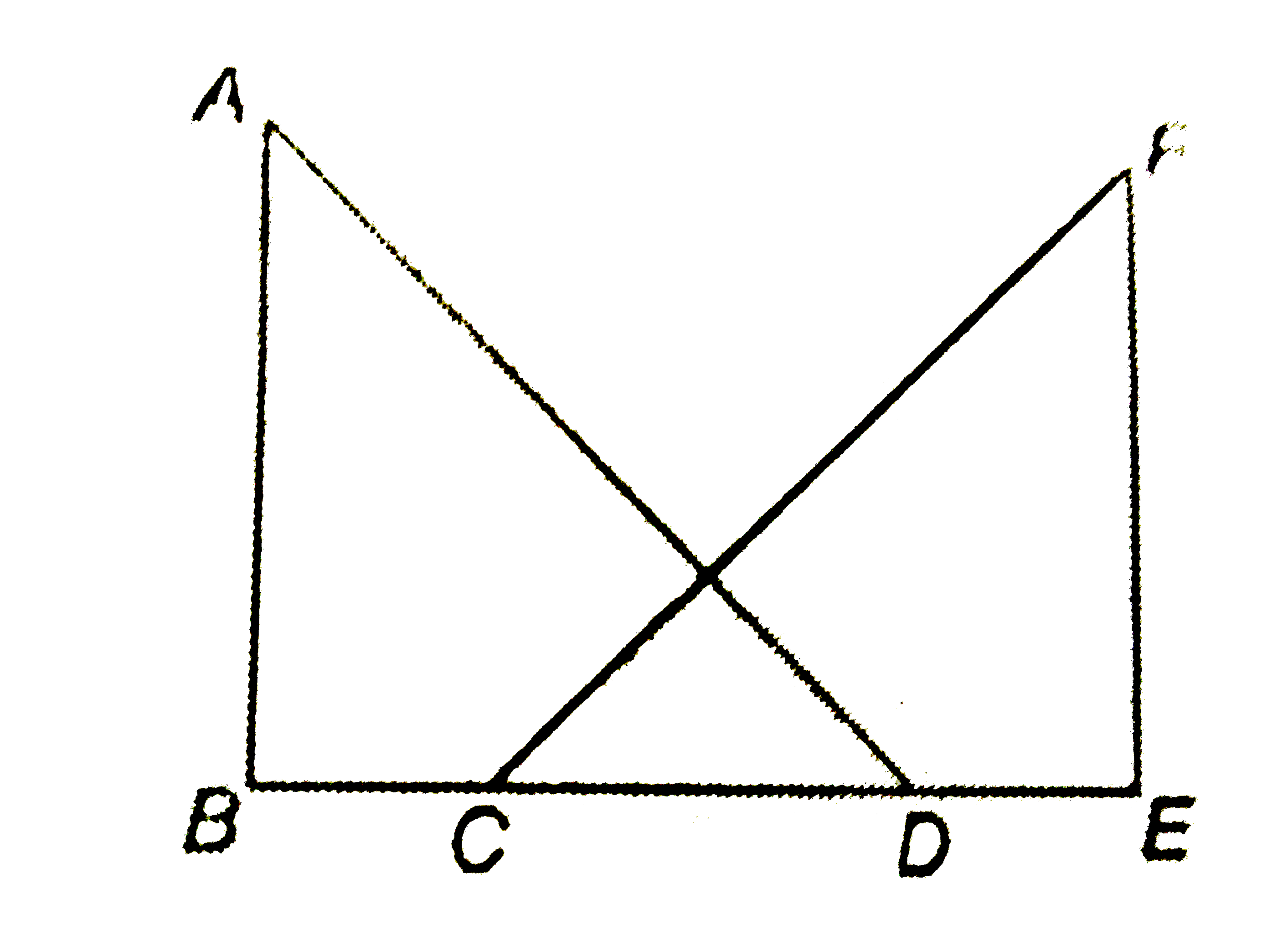
View SolutionIn the adjoining figure, ABCD is a parallelogram. If `angleMBC = angleNDA`, prove that `AM = NC`.
View SolutionIn the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the angles Q and R respectively of the triangle PQR. If `XS bot PQ`. Prove that :
(i) `DeltaXTQ cong DeltaXSQ`
(ii) PX bisects angle P.

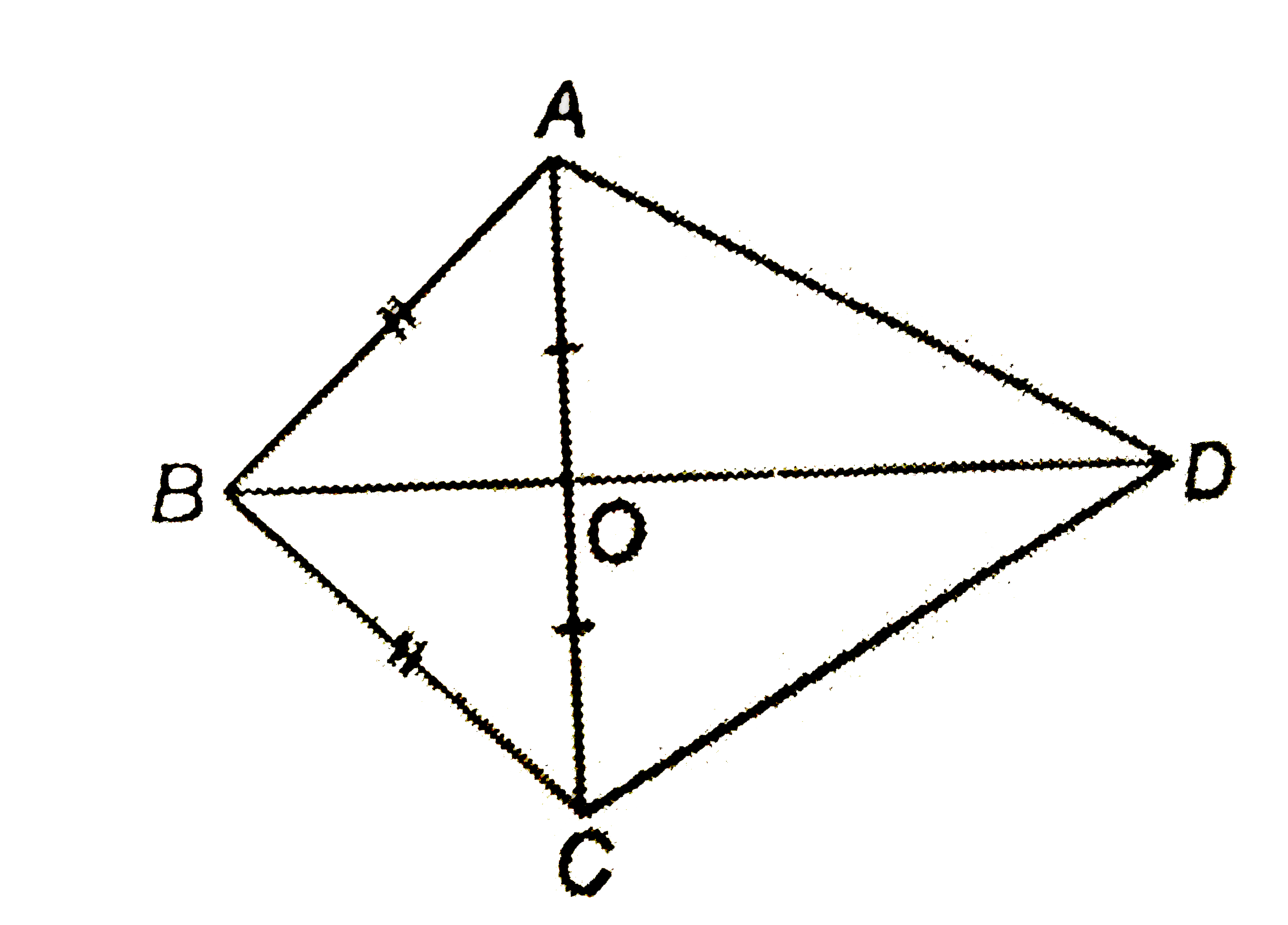
View SolutionIn the following figure, OA = OC and AB = BC. Prove that :
(i) `angleAPB=90^(@)`
(ii) `DeltaAOD cong DeltaCOD`
(iii) `AD = CD`
View SolutionIn the adjoining figure, ABCD is a paralogram. The side AB is produced to P such that AB=BP and the side AD is produced to Q such that AD = DQ. Prove that CP = CQ.
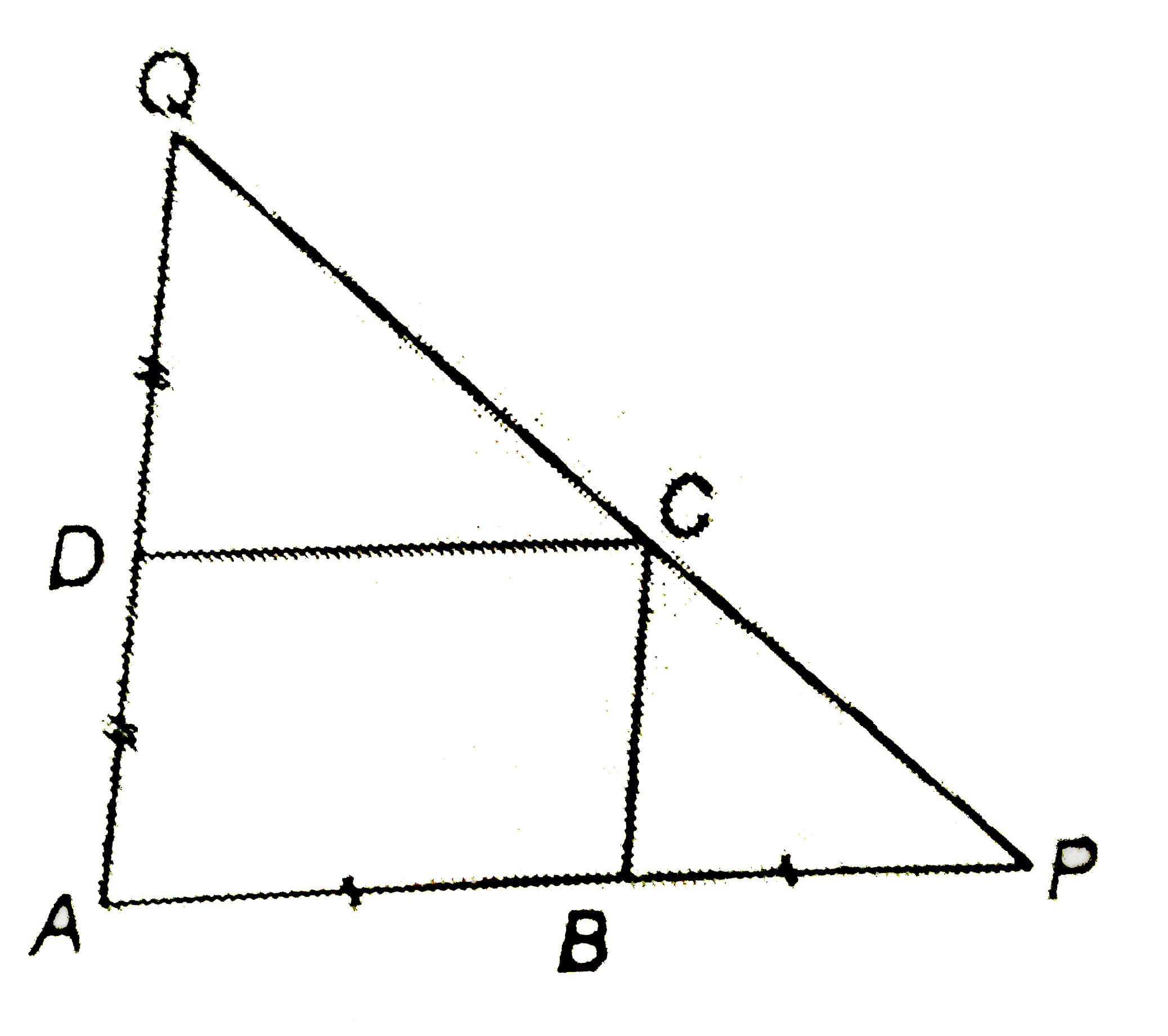
View SolutionIn the following figures, `AB=PQ, AC=PR` and `AM=PN`. Prove that `DeltaABC cong DeltaPQR`.
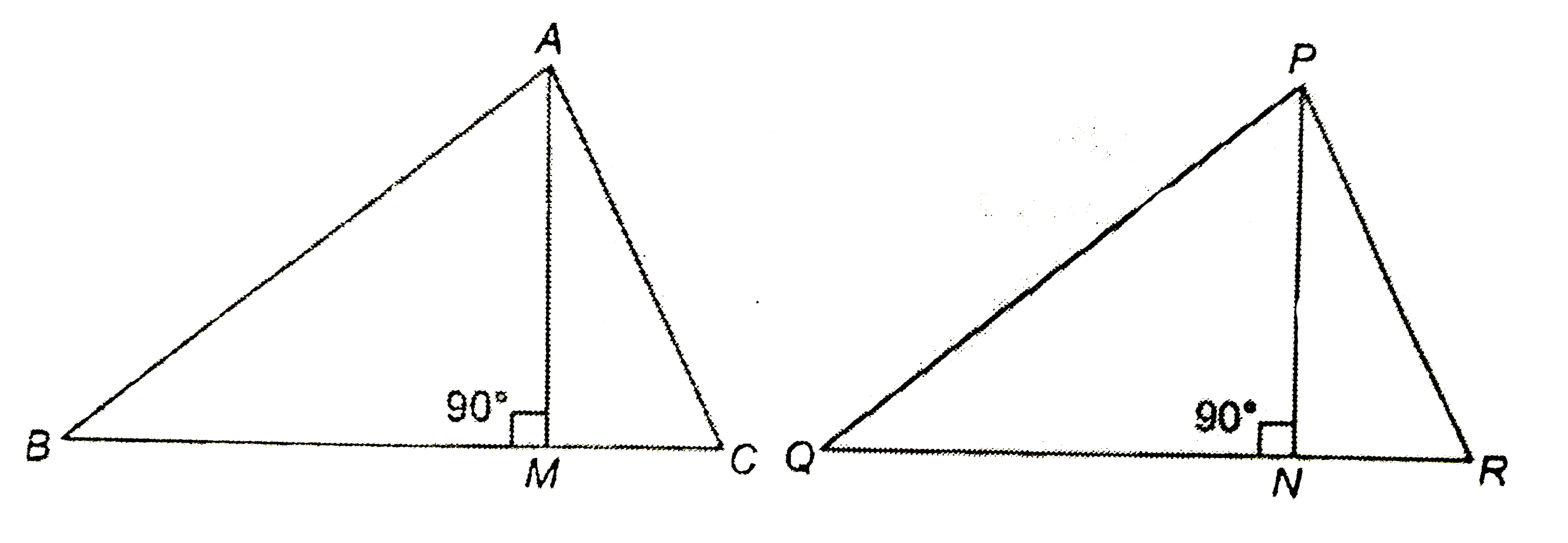
View SolutionProve that the medians of an equilateral triangle are equal.
View SolutionABCD is a square EF is parallel to BD. R is the mid-point of EF. Prove that :
(i) `BE = DF`
(ii) AR bisects angle BAD
(iii) If AR produced it will pass through C.

View SolutionThe following figure shows a triangle ABC in which Ab = AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that :
(i) AM = AN
(ii) `DeltaAMC cong DeltaANB`
(iii) `BN=CM`
(iv) `DeltaBMC cong DeltaCNB`

View SolutionIn the given figure, `AB"||"DC` and `angleD=angleC`. Prove that :
(i) `AD = BC`
(ii) `AC = BD`
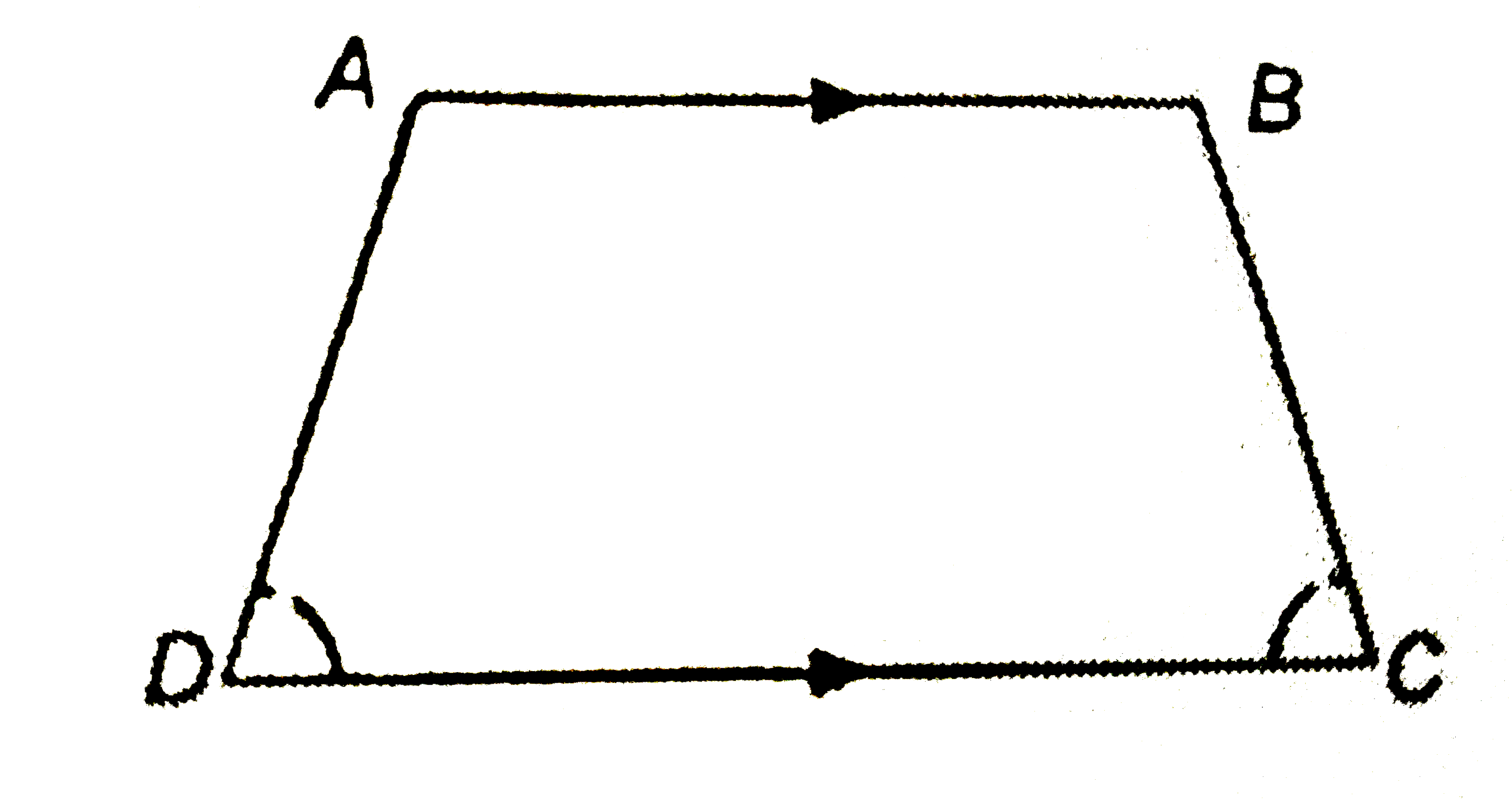
View SolutionIn the following figure, `AB||FD, AC||GE` and `BD = CE`. Prove that :
(i) BG=DF
(ii) CF=EG

View SolutionIn the adjoining figure, `angleAYZ=angleBYX=90^(@), AY = YZ` and `XY = BY`. Prove that `AB = ZX`.
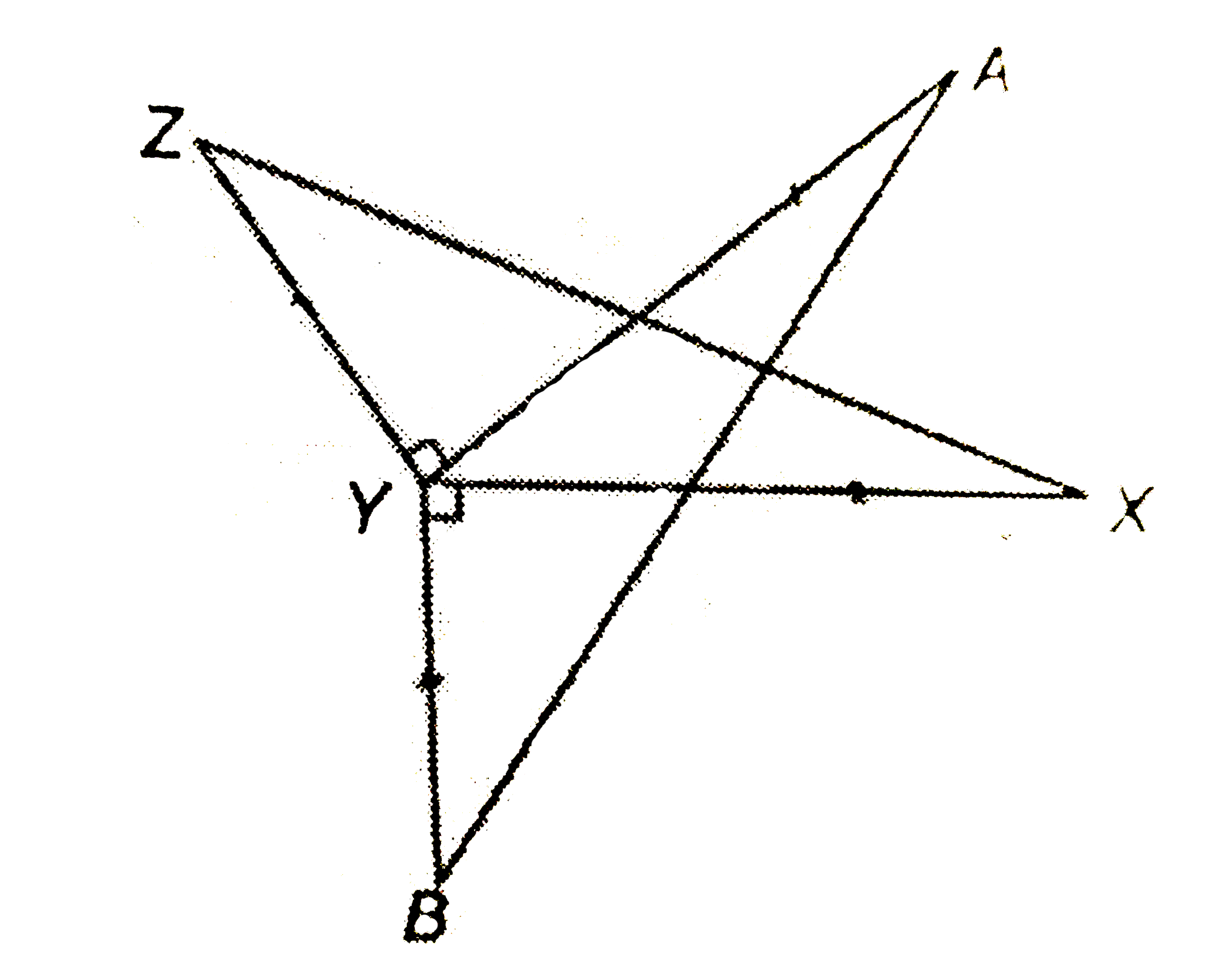
View SolutionIn the adjoining figure, ABCD is a square and PAB is an equilateral triangle. Find :
(i) `angleAPD`
(ii) `anglePDC`
(iii) `angleDPC`
(iv) Prove that `DP = CP`

View SolutionIn the adjoining figure, `DeltaABC` is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.

View Solution
Exercise 7a questions and complete solutions for chapter TRIANGLES of NAGEEN MATHS (HINGLISH) of Class 9