Complete Solutions to Solved Examples of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| NAGEEN PRAKASHAN | Solved Examples |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
In the given figure, prove that `AC = BD`.

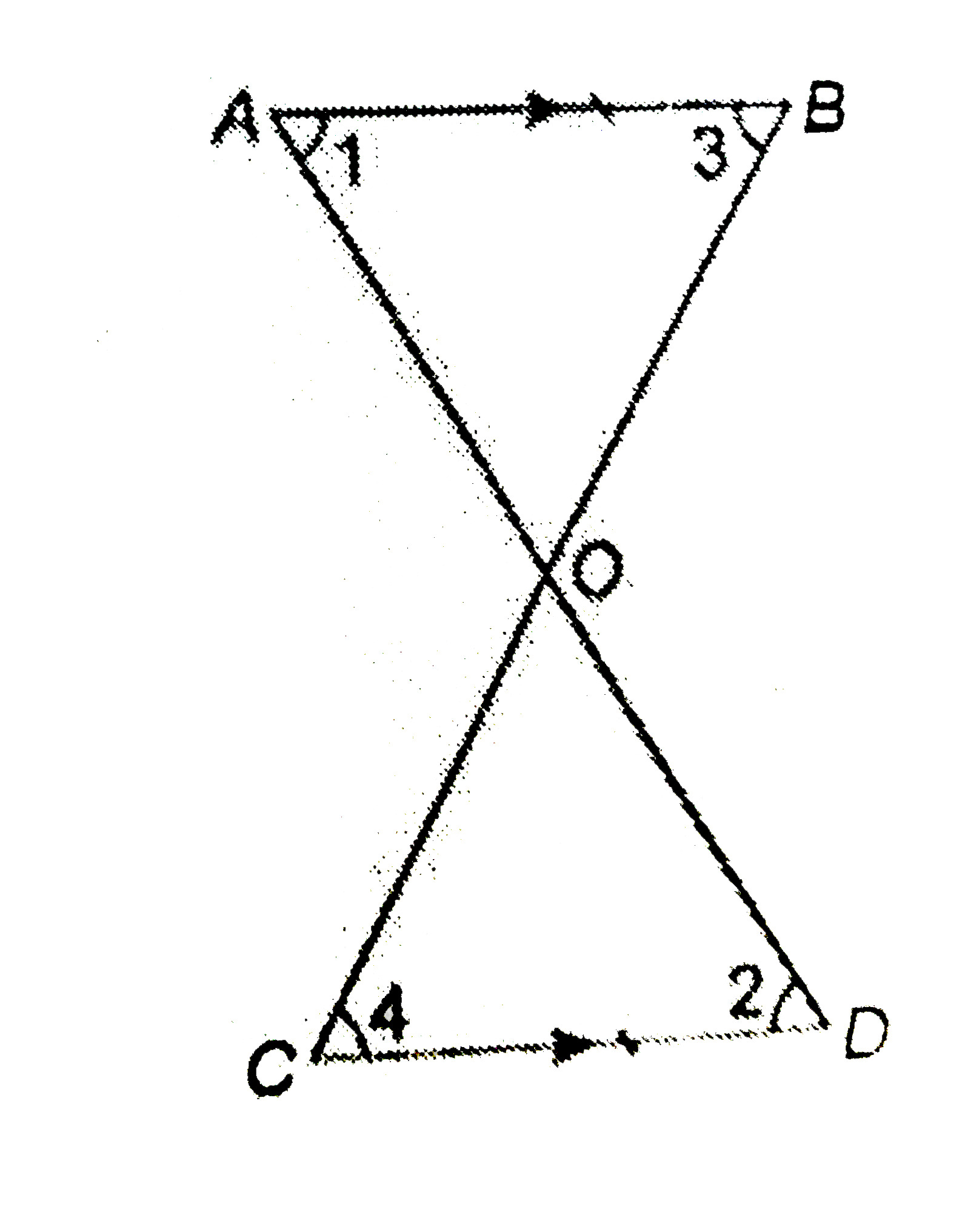
View SolutionIn the adjoining figure, AB = CD and AB||CD prove that
(i) `DeltaAOB cong DeltaDOC`
(ii) AD and BC bisect each other at the point O.
View SolutionThe sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and the median PM of triangle PQR respectively. Prove that the triangles ABC and PQR are congruent.
View SolutionIn the adjoining figure, BD = CE and `angleADB=angleAEC=90^(@)`, prove that
(i) `DeltaABD cong DeltaACE` (ii) ABC is an isosceles triangle.

View SolutionIn the adjoining figure, D is the mid-point of BC. If BM and CN are perpendiculars from B and C respectively on AD and AD produced, then prove that BM = CN.

View SolutionUse the information marked to prove :
(i) `DeltaEAC cong DeltaDBC` (ii) `EC = DC`
Also state the Euclid's axiom used in proving the congruency of two triangles.
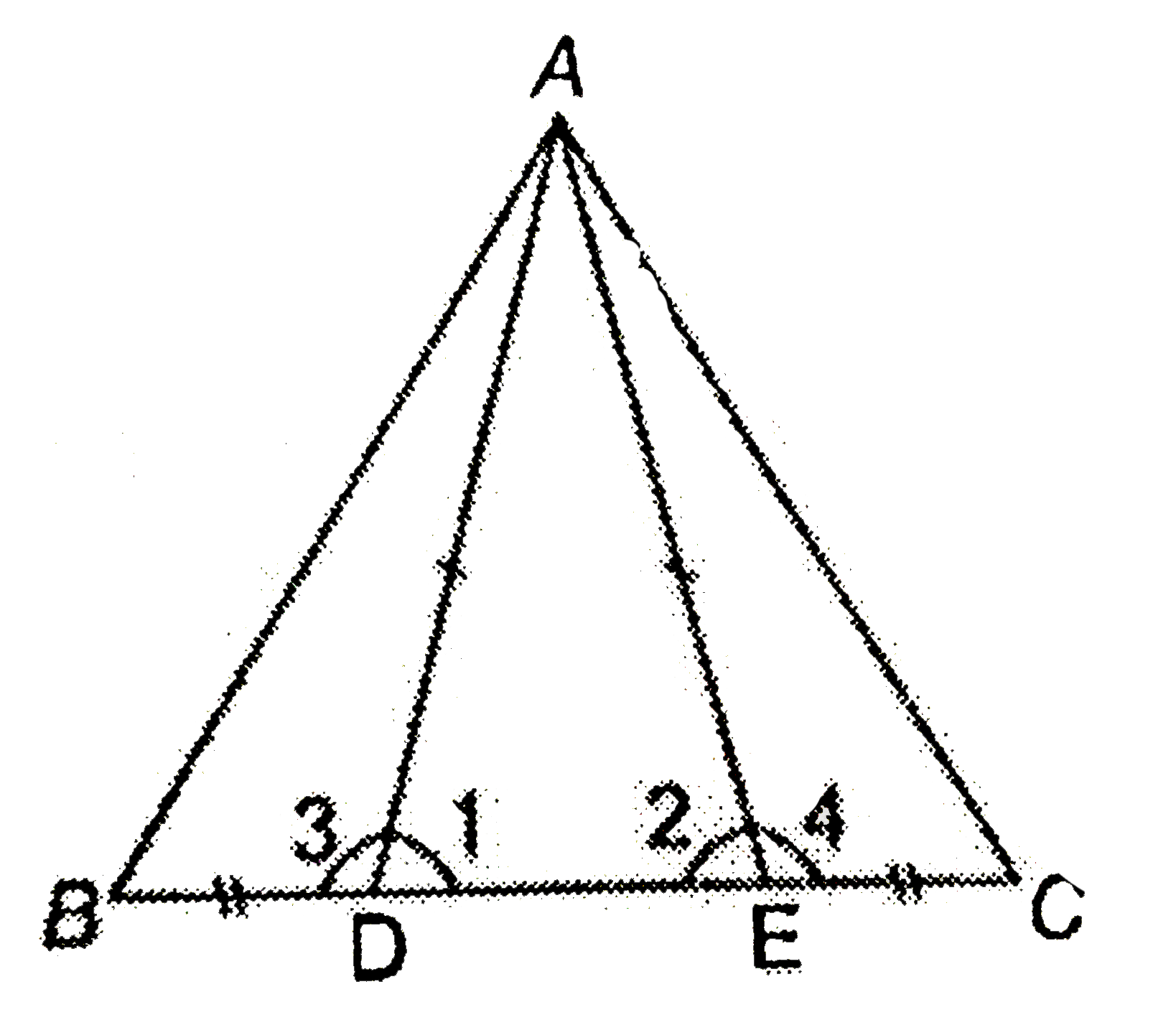
View SolutionIn the adjoining figure ABCD is a parallelogram, ABM is a line segment and E is the mid-point of BC. Prove that :
(i) `DeltaDCE cong DeltaMBe` (ii) `AB = BM`
(iii) `AM=2DC`
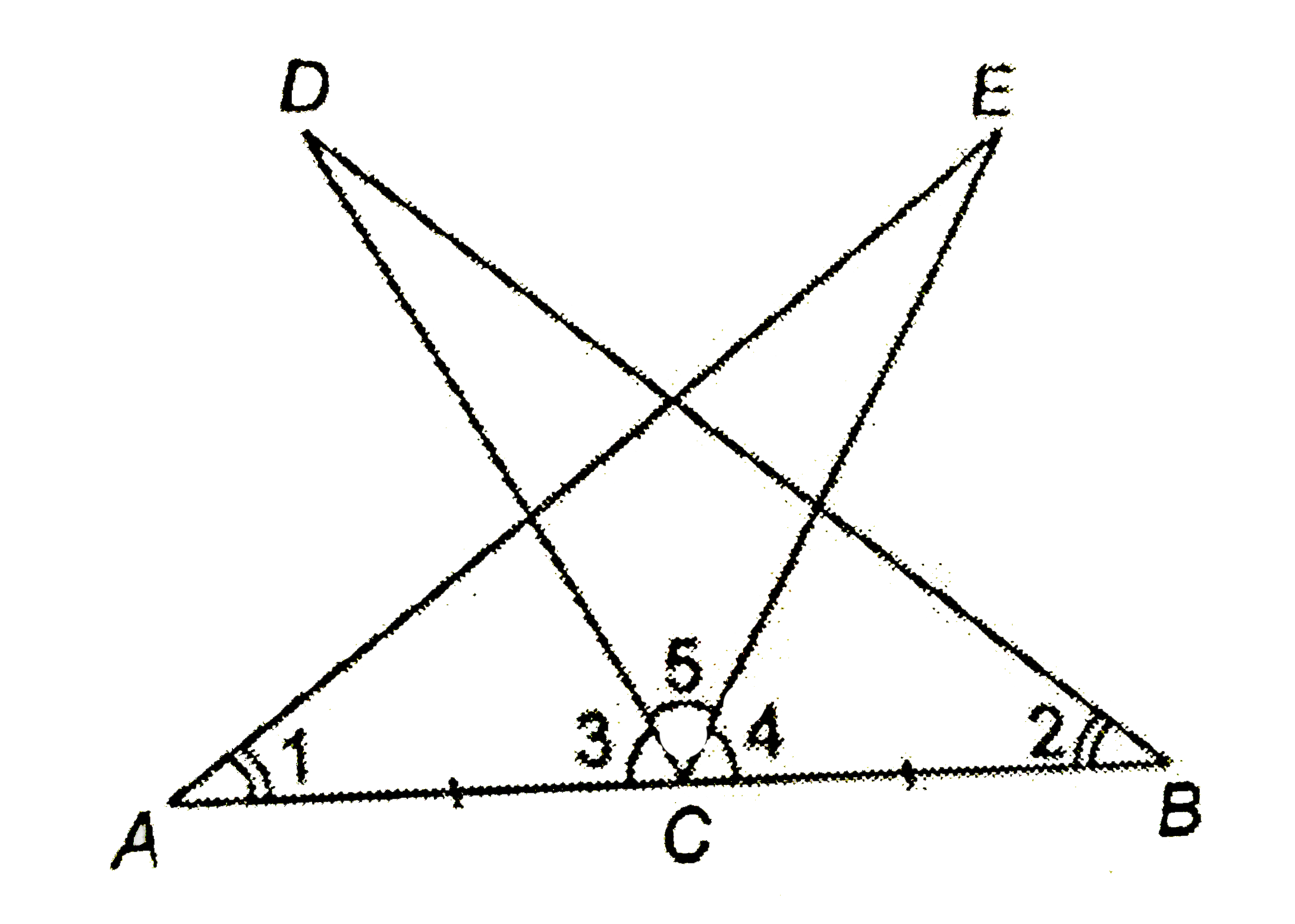
View SolutionIn the given figure, D and E are the points on the base BC of `DeltaABC` such that `BD=CE, AD= AE` and `angleADE=angleAED`, prove that `DeltaADB cong DeltaAEC`.
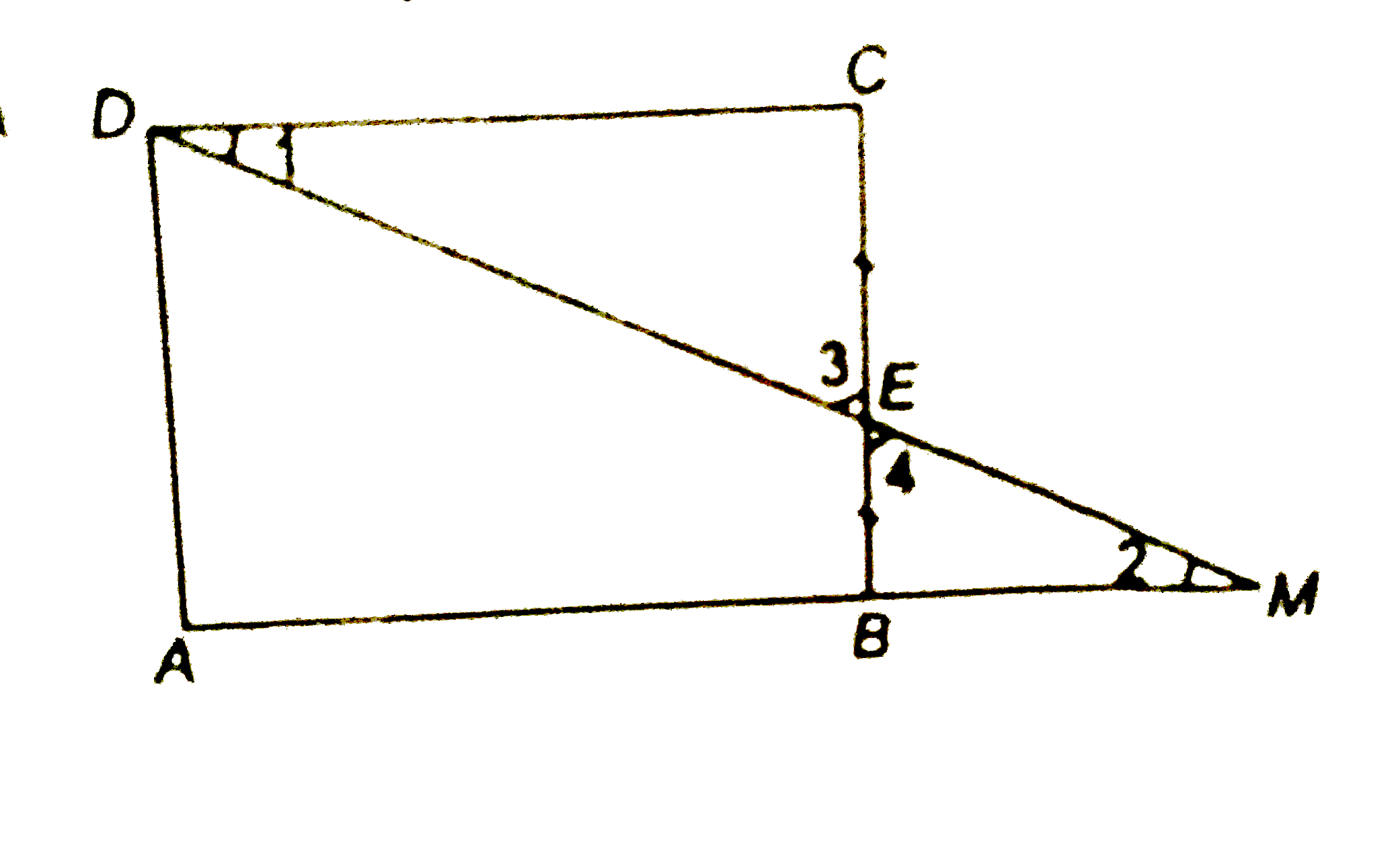
View SolutionIn the given figure, `PS=PR, angleTPS=angleQPR`. Prove that `PT=PQ`.
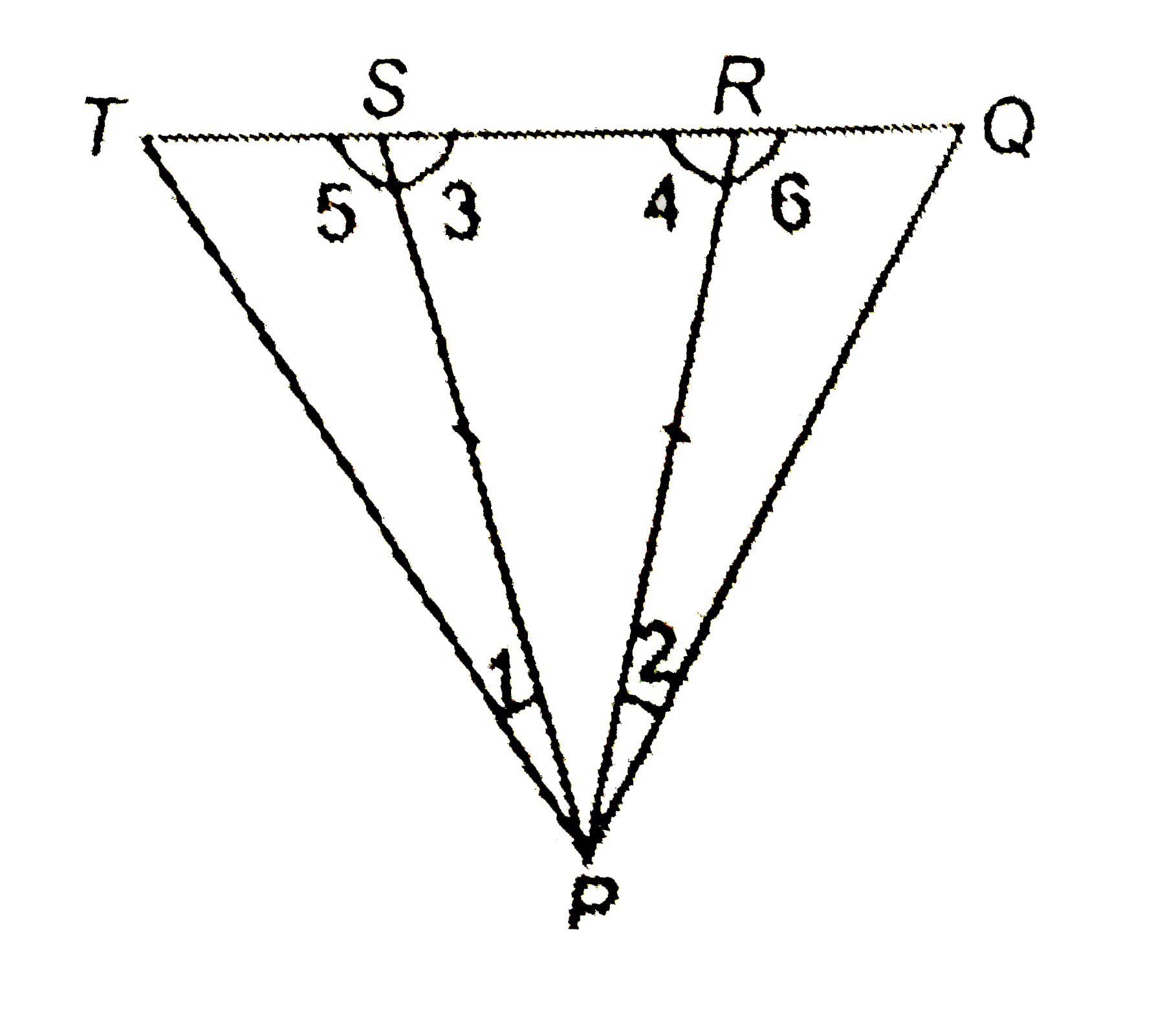
View SolutionIn right triangle ABC, right angle at C, M is the mid-point of the hydrotenuse AB. C is joined to M and produced to a point D such that `DM=CM`. Point D is joined to point B. Show that
(i) `DeltaAMC cong DeltaBMD` (ii) `angleDBC=angleACB`
(iii) `DeltaDBC cong DeltaACB` (iv) `CM=1/2 AB`
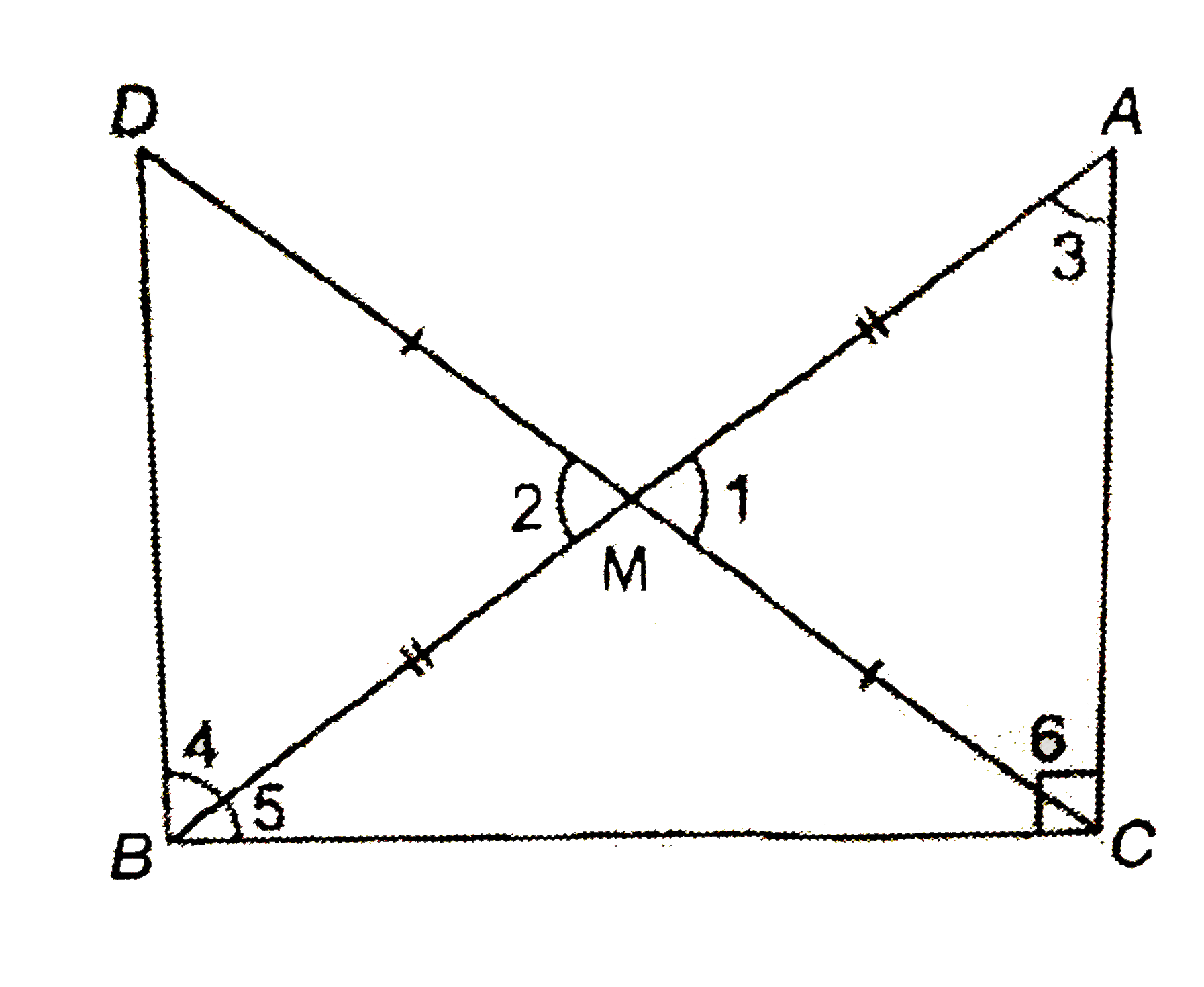
View SolutionIn the given figure, `AC=AE, AB=AD` and `angleBAD=angleEAC`. Prove that `BC=DE`.
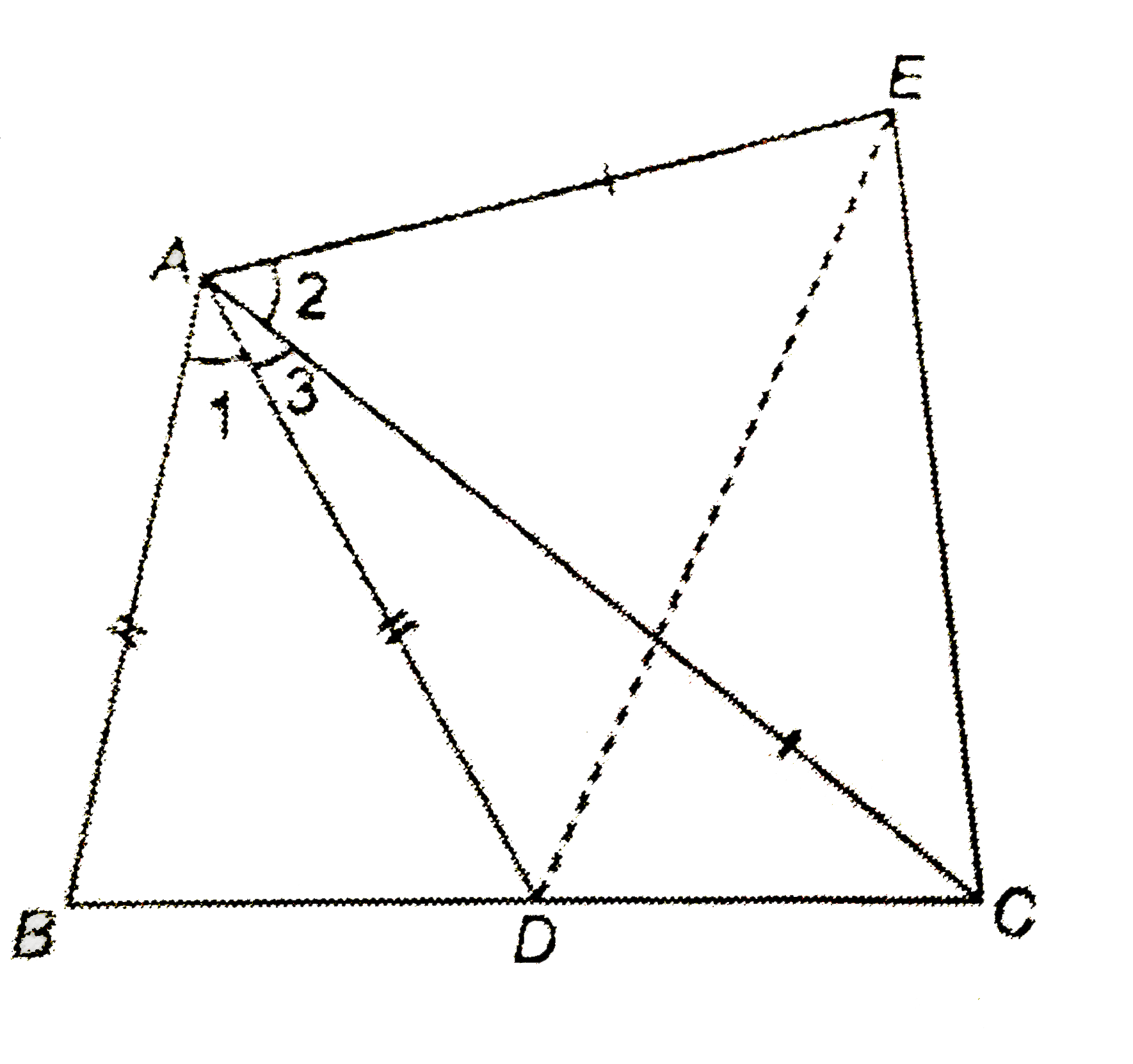
View SolutionIf the bisector of the vertical angle of a triangle bisects the base of the triangle. then the triangle is isosceles. GIVEN : A `A B C` in which `A D` is the bisector of `/_A` meeting `B C` in `D` such that `B D=D Cdot` TO PROVE : ` A B C` is an isosceles triangle.
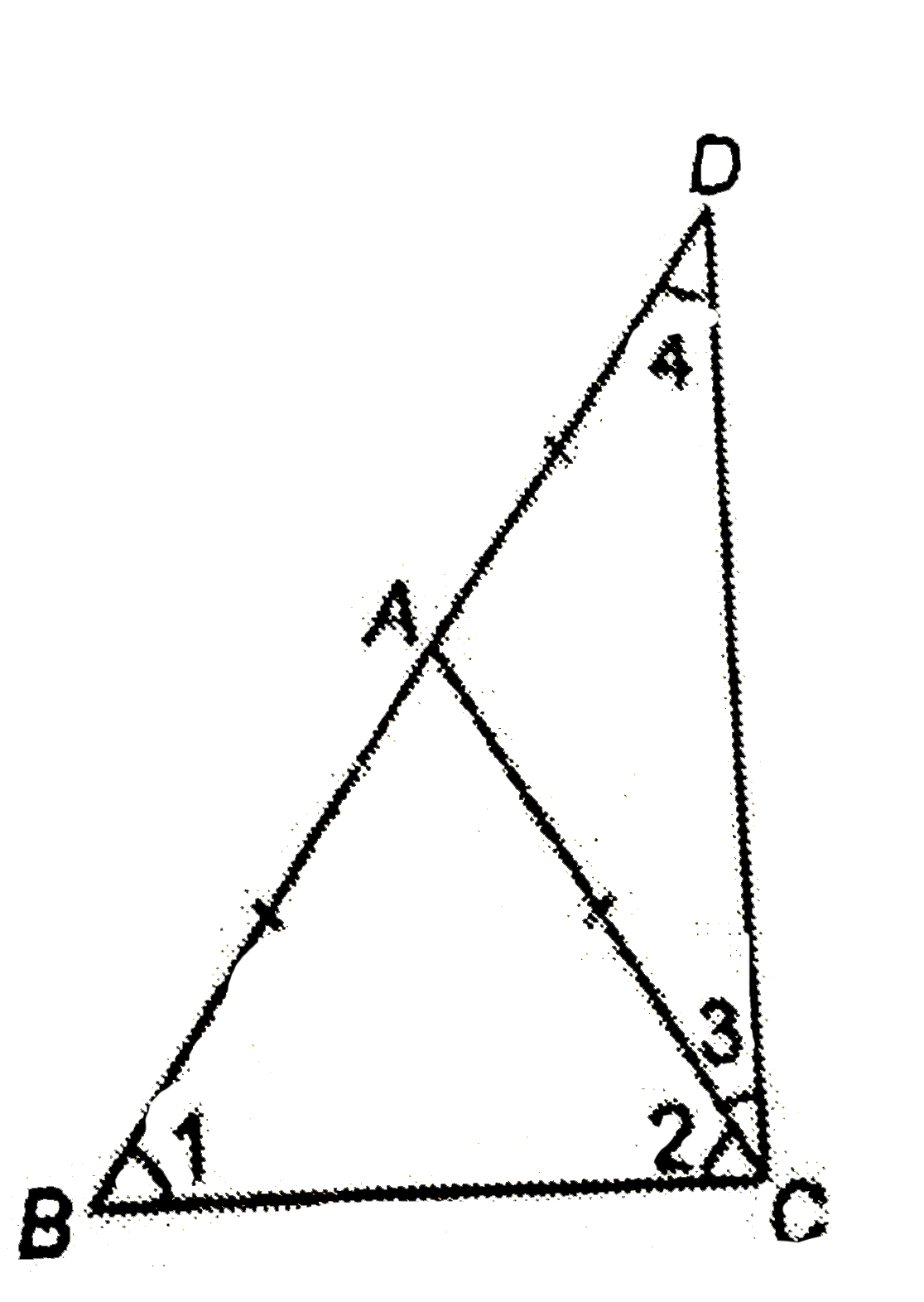
View Solution`DeltaABC` is an isosceles triangle with `AB=AC`, side BA is produced to `D` such that `AB=AD.` Prove that `angleBCD` is a right angle.
View SolutionIf `DeltaABC` is an isosceles triangle with AB = AC. Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

View SolutionIn the adjoining figure, find the measure of angle FEB, if the lengths of sides AD, DF and FE are equal and `angleACB=65^(@)`.

View Solution`A B C` is a triangle in which `/_B` =2 `/_CdotD` is a point on `B C` such that `A D` bisects `/_B A C` and `A B=C D` . Prove that `/_B A C=72^0dot`
View SolutionIn `DeltaABC, angleA=100^(@), angleC=30^(@)`. Find (i) largest side, (ii) smallest side of `DeltaABC`.
View SolutionIn `DeltaABC, D` is any point on side BC. Prove that
`AB+BC+CA gt 2AD`
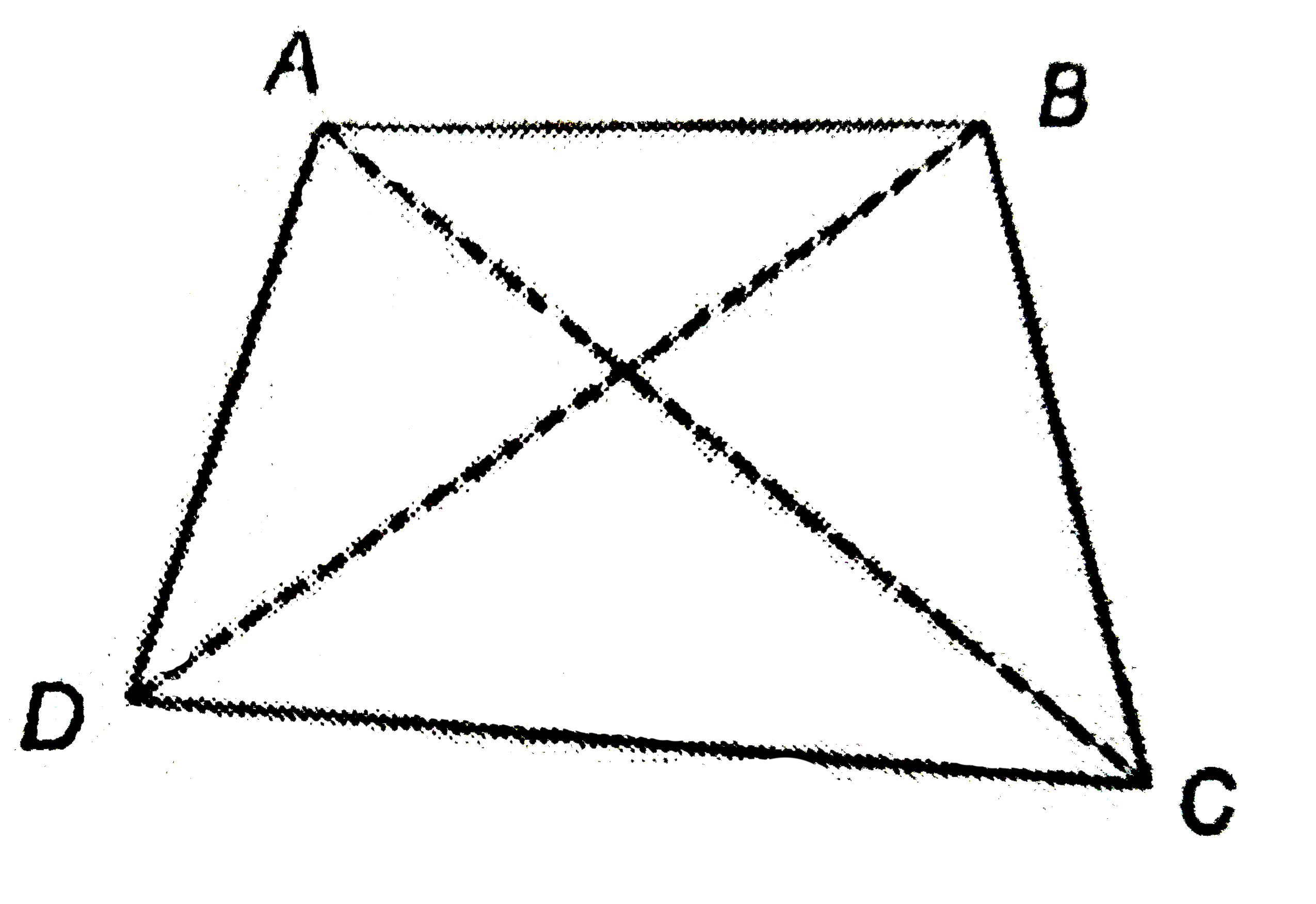
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) `AB+BC+CD+DA lt 2(AC+BD)`
(b) `AB+BC+CD+DA gt (AC+BD)`

View SolutionShow that the difference of any two sides in a triangle is smaller than the third side.
View SolutionIn `DeltaABC, BC=CA` and `angleA=40^(@)`. Find the largest side of `DeltaABD`.
View SolutionIn `DeltaABC, AD` is the bisector of `angleA`. Write AB, BD and DC in descending order of their length.

View SolutionIn `squareABCD, AB` is the smallest and CD is the largest side. Prove that :
(i) `angleB gt angleD` (ii) `angleA gt angle C`
View SolutionIf D any point on the BC of an isosceles triangle ABC then prove that `AB gt AD` and `AC gt AD`.

View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that `AD gt AB`.

View SolutionIn the adjoining figure, ABC is a triangle and D is any point in its interior. Show that `BD+DC lt AB +AC`.
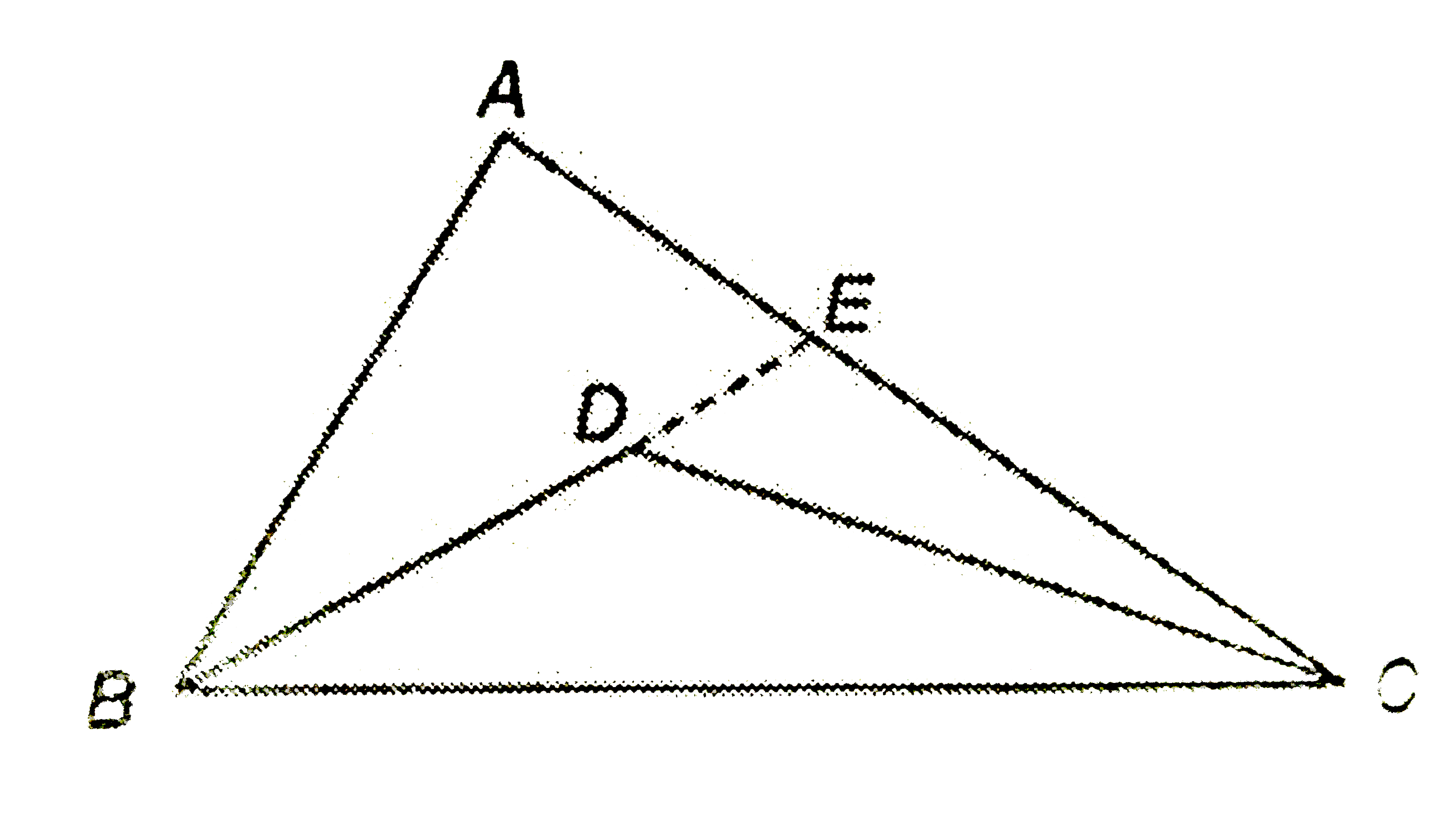
View SolutionProve that the perimeter of any triangle is greater than the sum of three altitudes.
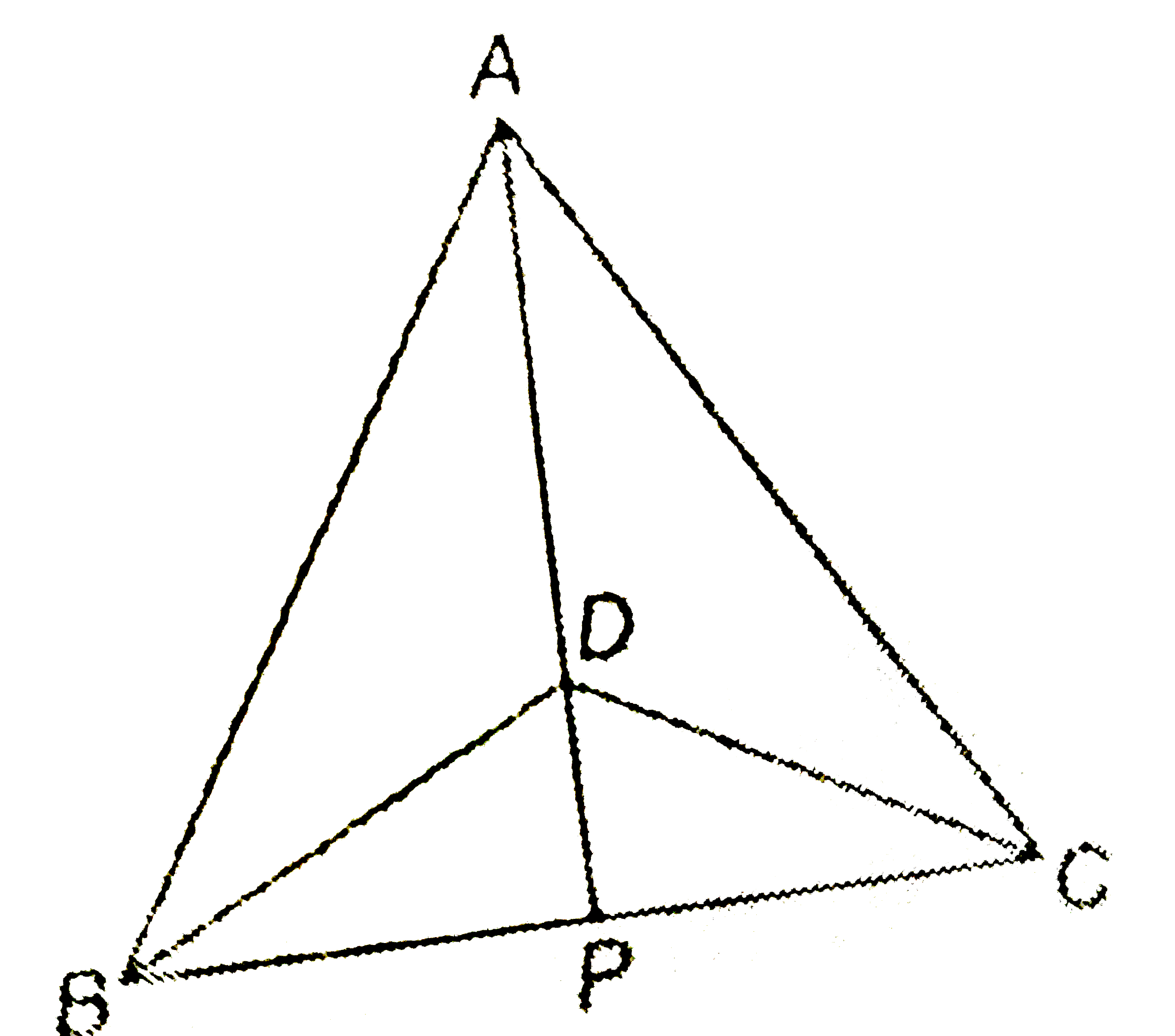
View Solution`DeltaABC` and `DeltaDBC` are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that :
(i) `DeltaABD cong DeltaACD`
(ii) `DeltaABP cong DeltaACP`
(iii) AP bisects `angleA` as well as `angleD`
(iv) AP is the perpendicular bisector of BC.
View SolutionIn figure, `angleB lt angleA` and `angleC lt angleD`. Show that `AD lt BC`.
View SolutionS is any point on side QR of a `DeltaPQR`. Show that `PQ+QR+RP gt 2PS`.
View SolutionBisector of the angles B and C of an isosceles triangle ABC with Ab = AC intersect each other at O. Shown that external angle agjacent to `angleABC` is equal to `angleBOC`.
View SolutionProve that sum of any two sides of a triangle is greater than twice the median with respect to the third side.
View SolutionShow that in a quandrilateral `ABCD, AB + BC + CD+ DA lt 2 (BD+AC)`.
View Solution
Solved Examples questions and complete solutions for chapter TRIANGLES of NAGEEN MATHS (HINGLISH) of Class 9