Complete Solutions to EXERCISE 8.1 of chapter QUADRILATERALS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | QUADRILATERALS |
| Mathematics | EXERCISE 8.1 |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
If the two diagonals of a parallelogram are equal; it is a rectangle.
View SolutionShow that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
View SolutionThe angles of a quadrilateral are in the ratio `3\ :\ 5\ :\ 9\ :\ 13`. Find all the angles of the quadrilateral.
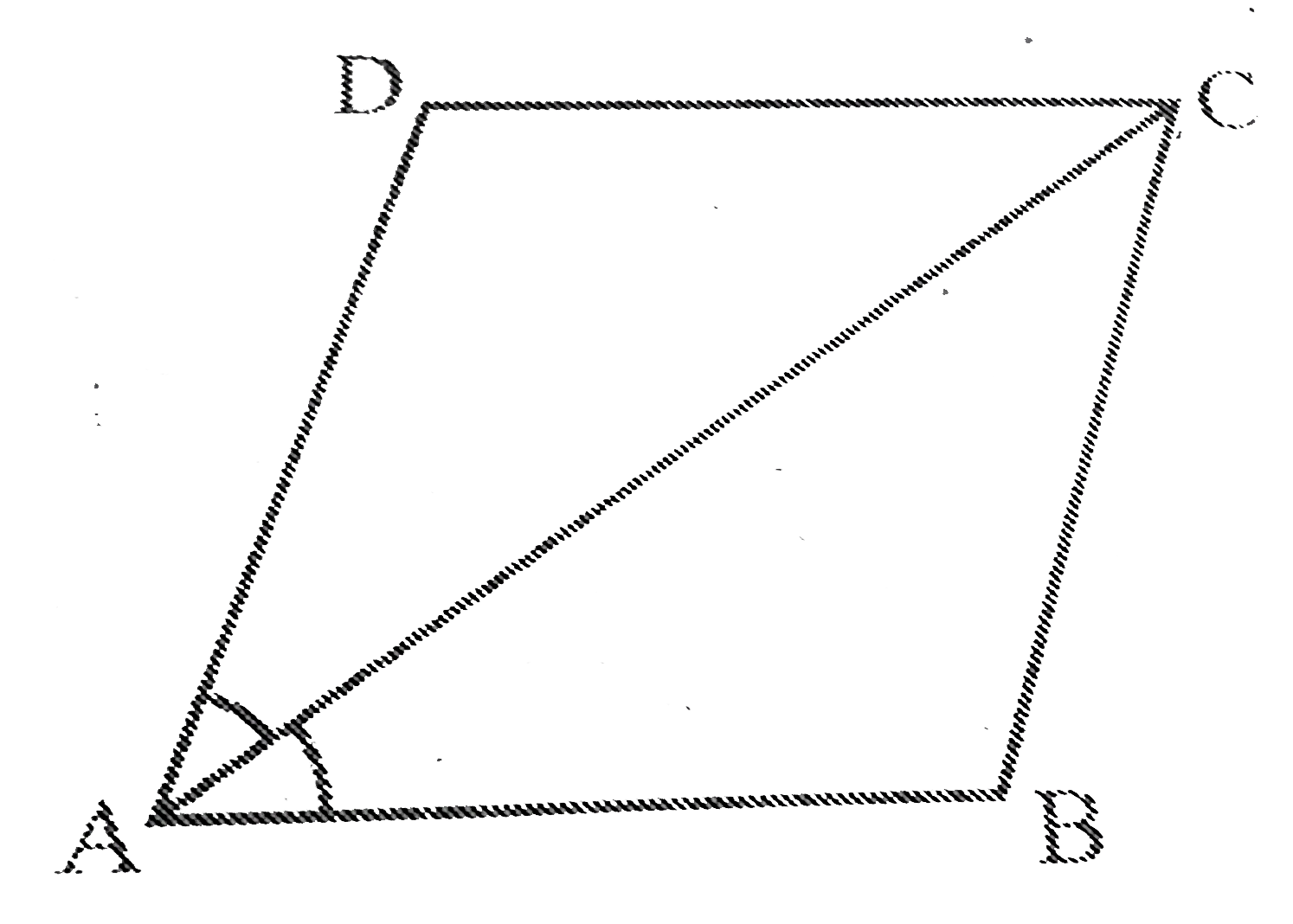
View SolutionDiagonal AC of a parallelogram ABCD bisects `\ /_A`. Show that
(i) it bisects `\ /_C` also,
(ii) ABCD is a rhombus.
View Solution`A B C D` is a rhombus. Show that diagonals `A C` bisects `/_A` as well as `/_C` and diagonal `B D` bisects `/_B` as well as `/_D`
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that if the diagonals of a quadrilateral are equal and bisect each other at right angle, then it is a square.
View SolutionABCD is a rectangle in which diagonal AC bisects `/_A` as well as `/_C` . Show that: (i) ABCD is a square (ii) diagonal BD bisects `/_B` as well as `/_Ddot` .
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that `D P = B Q`. Show that:
(i) `DeltaA P D~= DeltaC Q B`
(ii) `A P = C Q`
(iii) `DeltaA Q B~= DeltaC P D`
(iv) `A Q = C P`
(v) APCQ is a parallelogram.

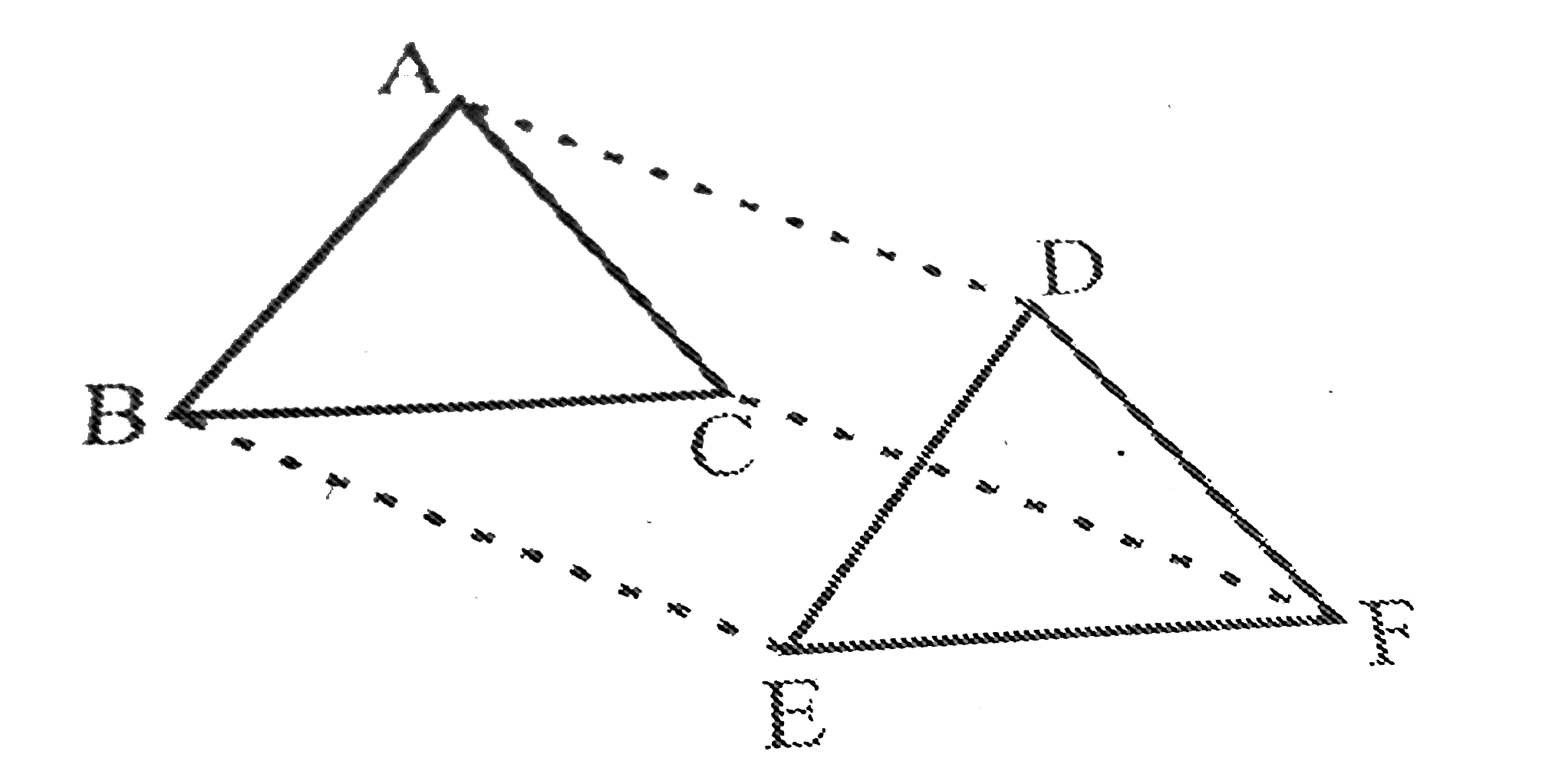
View SolutionIn `DeltaA B C`and `DeltaD E F`, `A B\ =\ D E`, `A B\ ||\ D E`, `B C\ =\ E F` and `B C\ ||\ E F`. Vertices A, B and C are joined to vertices D, E and F respectively (see Fig. 8.22).Show that
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ ABC ≅ ∆ DEF.
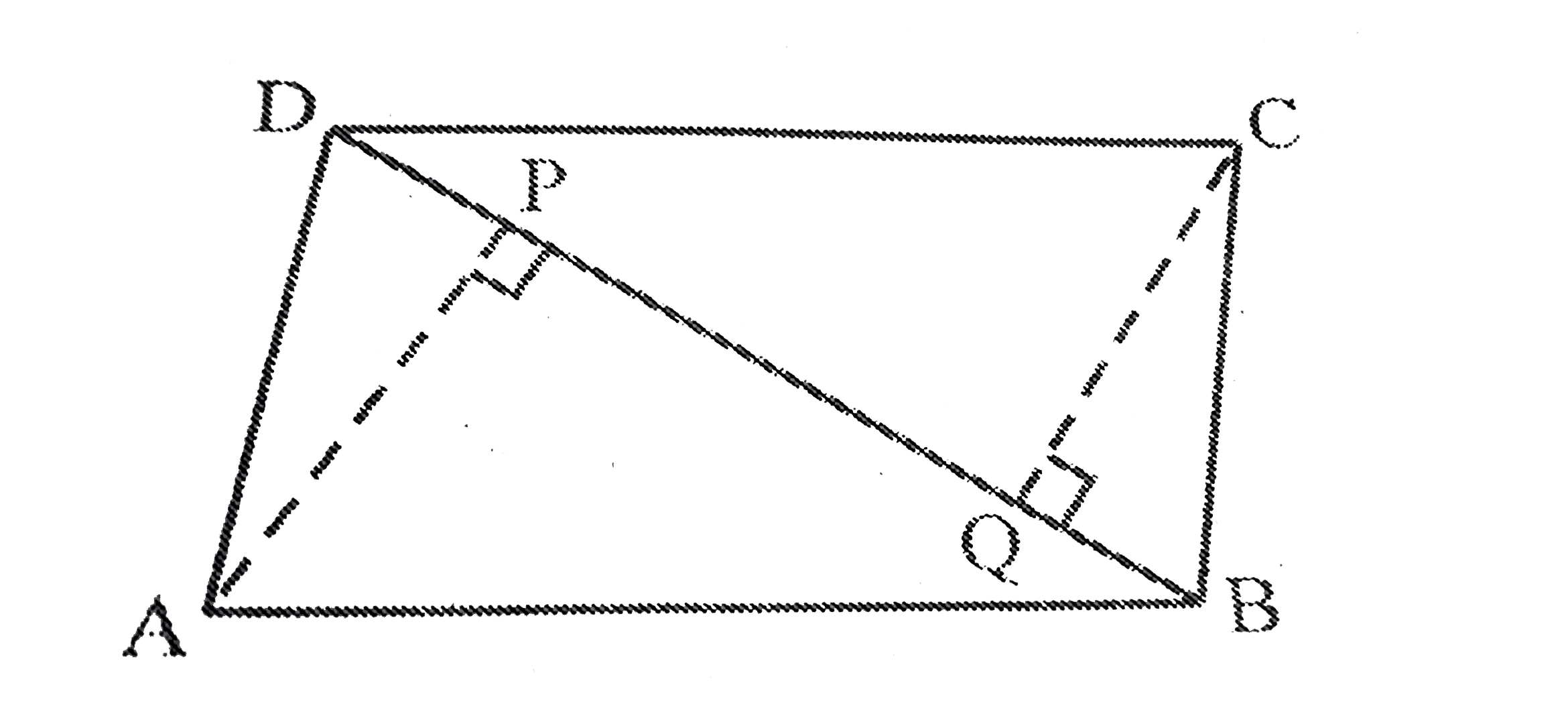
View SolutionABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD . Show that
(i) `DeltaA P B~=\ DeltaC Q D`
(ii) `A P\ =\ C Q`
View SolutionIn Figure, `A B C D` is a trapezium in which `A B || C D` and `A D=B C`. Show that :
(i) `/_A=/_B`
(ii) `/_C=/_D`
(iii) ` A B C~= B A D`
(iv) diagonal `A C=d i agon a lB D`
View Solution
EXERCISE 8.1 questions and complete solutions for chapter QUADRILATERALS of NCERT MATHEMATICS(ENGLISH) of Class 9