Complete Solutions to Areas Of Parallelograms And Triangles of chapter Areas of Parallelograms and Triangles of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | Areas of Parallelograms and Triangles |
| NCERT EXEMPLAR | Areas Of Parallelograms And Triangles |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
The median of a triangle divides it into two
View SolutionIn which of the following figures, you find two polygons on the same base and between the same parallels?
View SolutionThe figure obtained by joining the mid-points of the adjacent sides of a rectangle of sides 8 cm and 6 cm, is
View SolutionIn the figure, the area of parallelogram ABCD is

View SolutionIn figure, if parallelogram ABCD and rectangle ABEM are of equal area, then
View SolutionThe mid-point of the sides of triangle along with any of the vertices as the fourth point make a parallelogram of area equal to
View SolutionTwo parallelograms are on equal bases and between the same parallels.
The ratio of their areas is
View SolutionABCD is a quadrilateral whose diagnonal AC divides it into two parts, equal in are, then ABCD
View SolutionIf a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is
View SolutionIn a trapezium ABCD, AB || DC, AB = a cm, and DC = b cm. If M and N are the midpoints of the nonparallel sides, AD and BC respectively then find the ratio of ar(DCNM) and ar(MNBA).
View SolutionABCD is a parallelogram and X is the mid-point of AB. `(AXCD)= 24 cm^(2)`, then `ar (ABC) = 24 cm^(2)`.
View SolutionPQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm and A is any point on PQ. If PS = 5 cm, then ar `(DeltaPAS) = `.
View SolutionPQRS is a parallelogram whose area is `180 cm^(2)` and A is any point on the diagonal QS. The area of `DeltaASR?`
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, `ar (DeltaBDE) = (1)/(2) ar (DeltaABC)`.
View SolutionIn the figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then, `ar (DeltaDPC) = ar (EFGD)`.
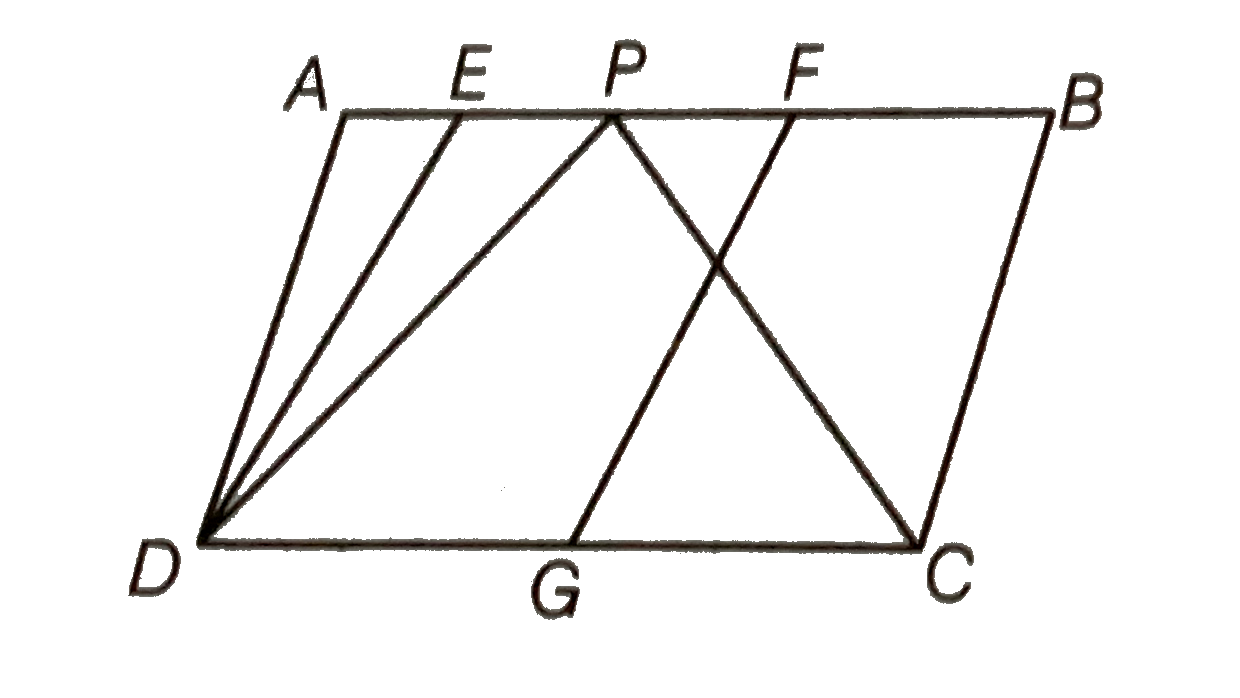
View SolutionIn the figure, PSDA is a parallelogram. Points Q and R are taken on PS such that `PQ = QR = RS " and " PA || QB || RC`. Prove that `ar (PQE) = ar (CFD)`.
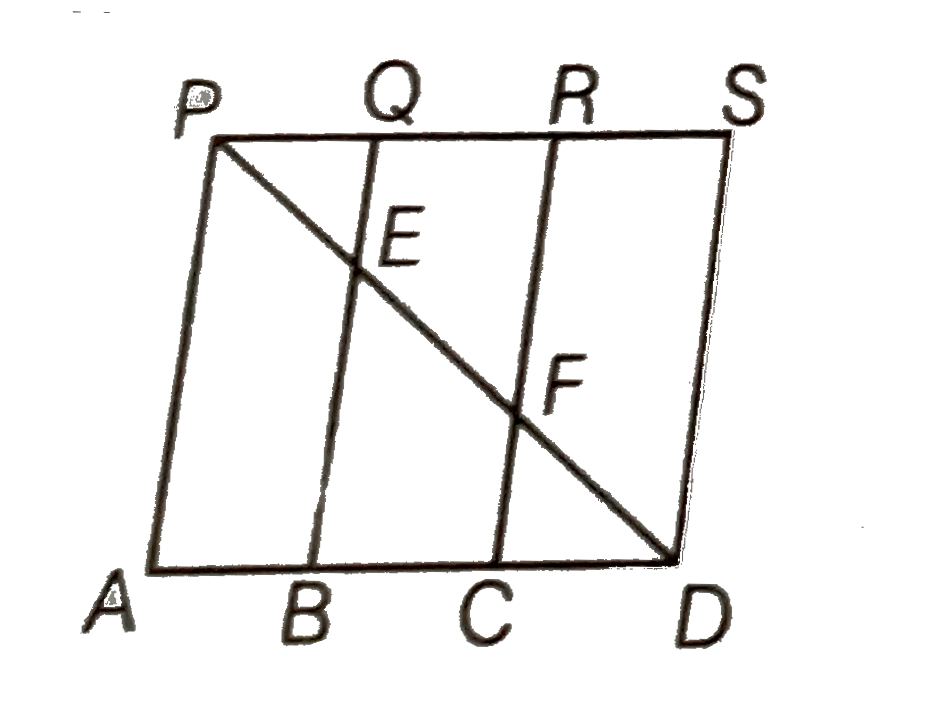
View SolutionX and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z (see figure). Prove that `ar (DeltaLZY) = ar (MZYX)`.
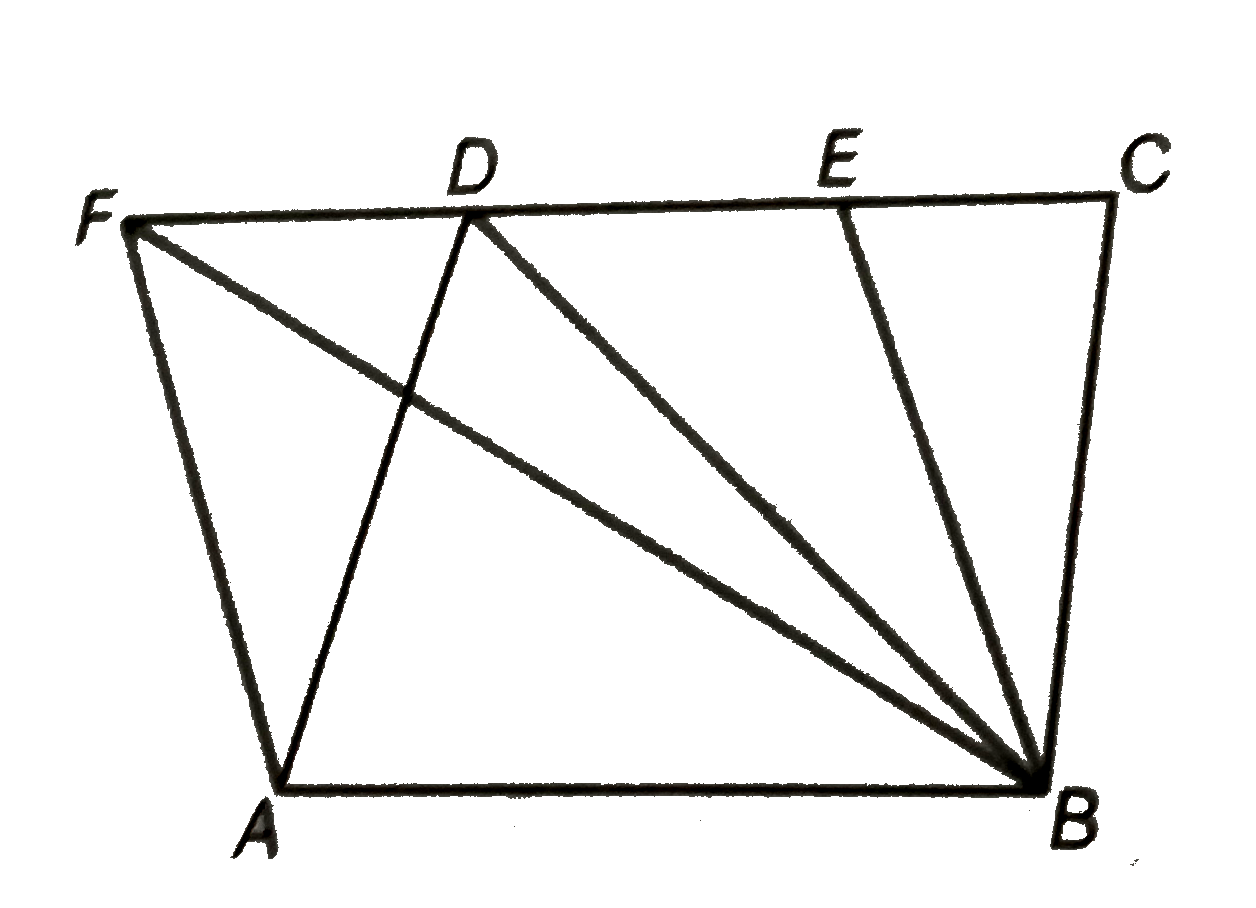
View SolutionThe area of the parallelogram ABCD is `90 CM^(2)`. Find
(i) ar (ABEF) (ii) ar `(DeltaABD)`
(iii) ar `(DeltaBEF)`
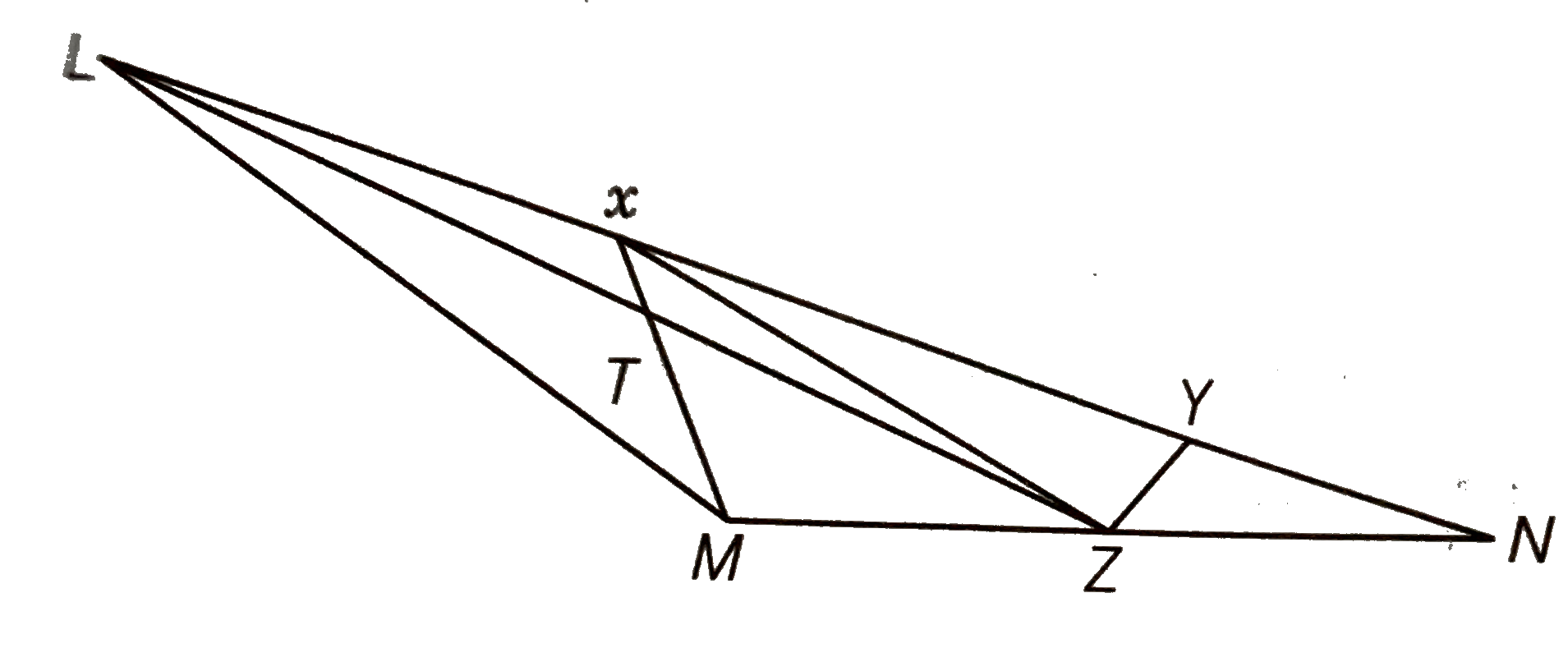
View SolutionIn `Delta` ABC, D is the mid-point of AB and P is any point on BC. If `CQ || PD` meets AB and Q (shown in figure), then prove that
`ar (DeltaBPQ) = (1)/(2) ar (DeltaABC)`.

View SolutionABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that `ar (DeltaAER) = ar (DeltaAFR)`.

View SolutionO is any point on the diagonal PR of a parallelogram PQRS (figure). Prove that `ar (DeltaPSO) = ar (DeltaPQO)`.

View SolutionABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F.
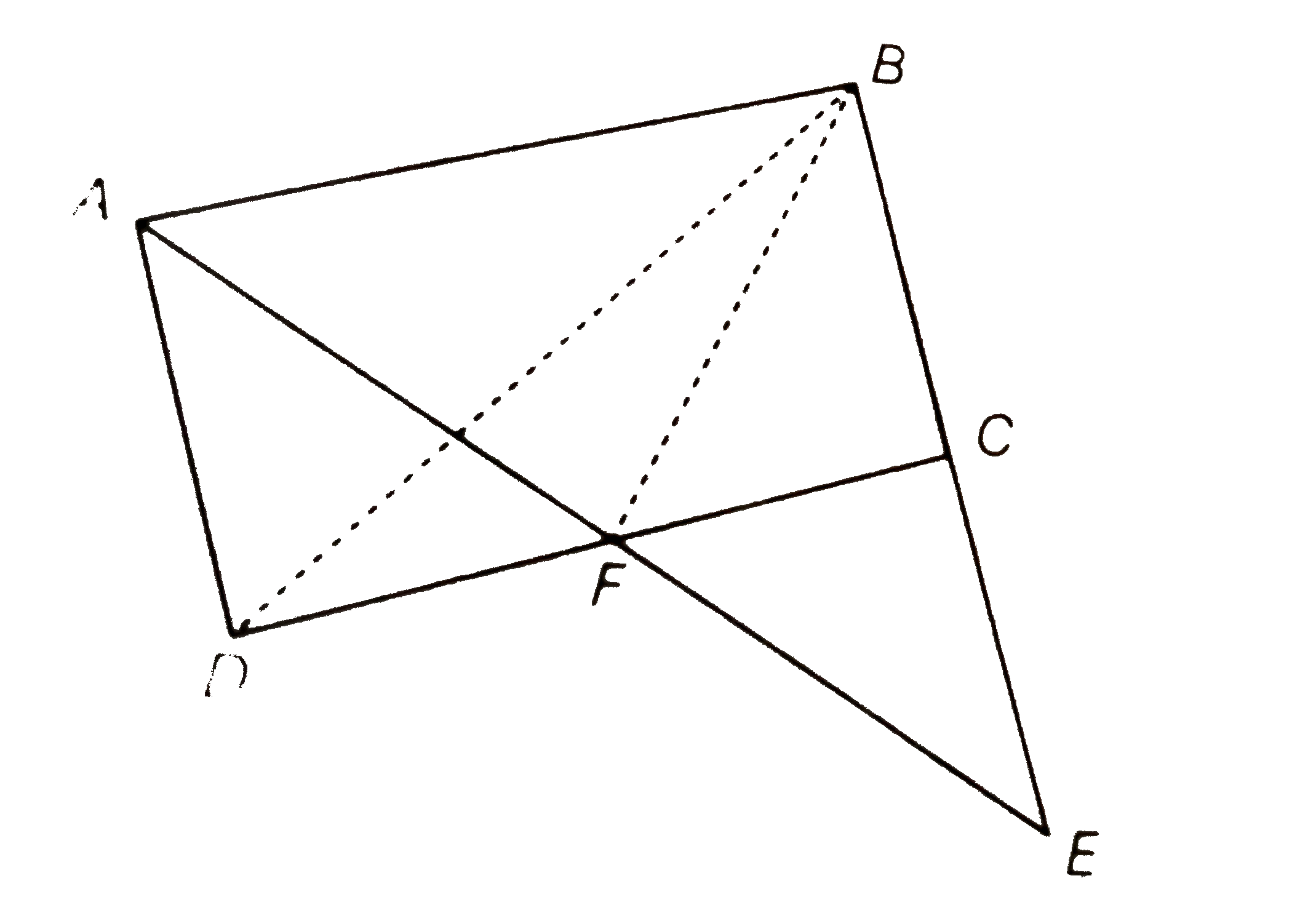
If `ar (DeltaDFB) = 3 cm^(2)`, then find the area of the parallelogram ABCD.
View SolutionIn trapezium ABCD, `AB || DC` and L is the mid-point of BC. Through L, a line `PQ || AD` has been drawn which meets AB in P and DC produced in Q. Prove that ar (ABCD) = ar (APQD).

View SolutionIf the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram, so formed will be half of the area of the given quadrilateral (figure).

View SolutionA point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that `ar(DeltaADF) = ar (ABFC)`.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line a drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionThe median BE and CF of a triangle ABC intersect at G. Prove that the area of `DeltaGBC =` area of the quadrilateral AFGE.
View SolutionIn figure, `CD || AE` and `CY || BA`. Prove that `ar (DeltaCBX) = ar (DeltaAXY)`.

View SolutionABCD is trapezium in which `AB||DC`, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that
`ar (DCYX) = (7)/(9) ar (XYBA)`.
View SolutionIn `DeltaABC` , if L and M are the points on AB and AC, respectively such that `LM || BC`. Prove that `ar (DeltaLOB) = ar (DeltaMOC)`.
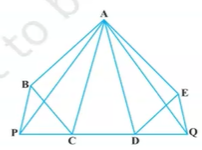
View SolutionIn figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that `ar (ABCDE) = ar (DeltaAPQ)`.
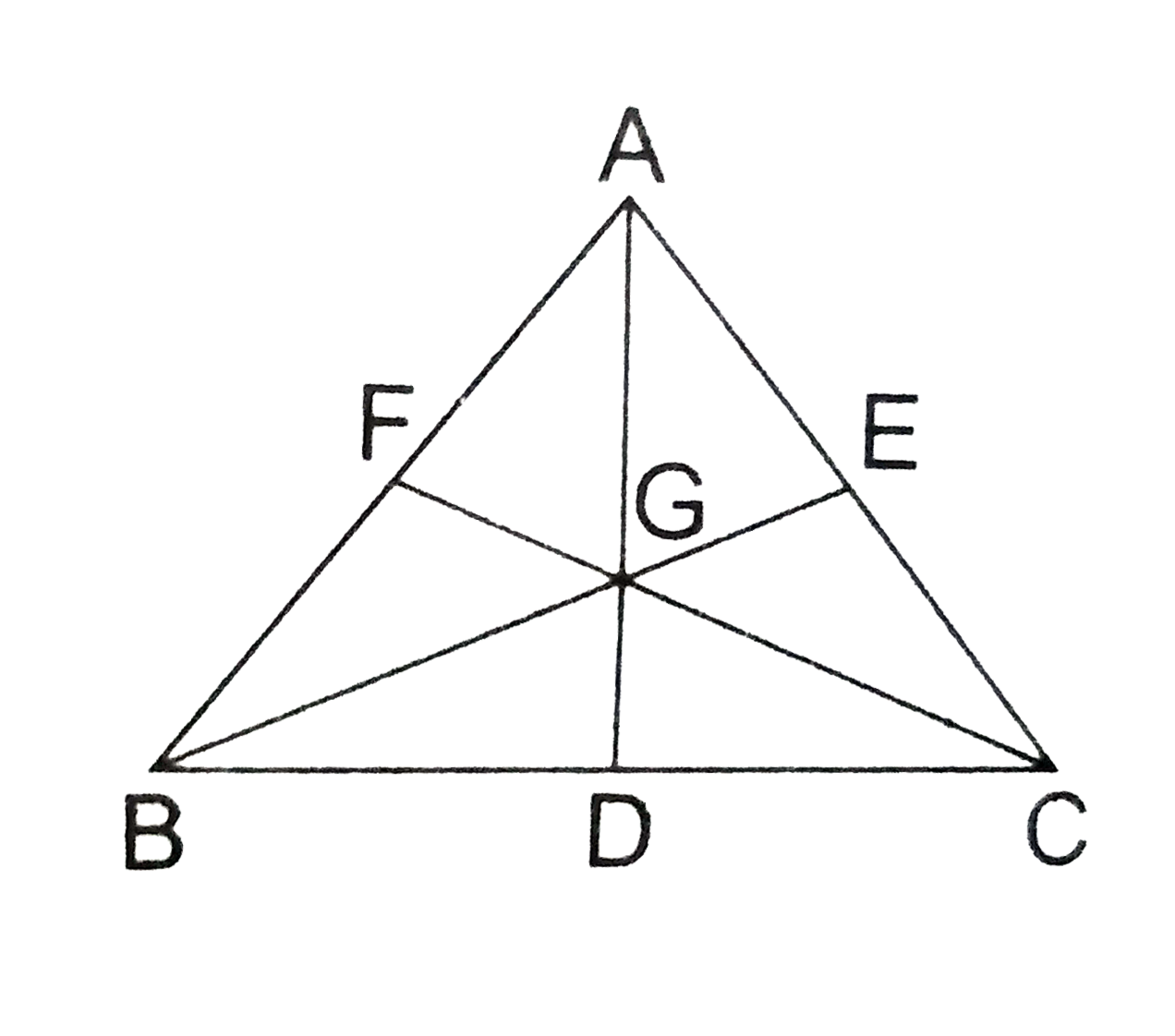
View SolutionIf the medians of a `triangle`ABC intersect at G, show that
`ar(triangleAGB)=ar(triangleAGC)=ar(triangleBGC)`
`=(1)/(3)ar(triangleABC)`.
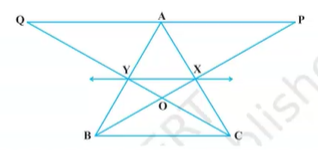
View SolutionIn figure X and Y are the mid-points of AC and AB respectively, `QP || BC` and CYQ and BXP are straight lines. Prove that `ar (DeltaABP) = ar (DeltaACQ)`.
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that `ar (DeltaPEA) = ar (DeltaQFD)`.
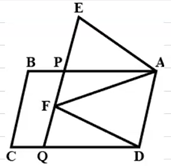
View Solution
Areas Of Parallelograms And Triangles questions and complete solutions for chapter Areas of Parallelograms and Triangles of NCERT MATHS (HINGLISH) of Class 9
