Competition File (Assertion Reason Type Questions) from MODERN PUBLISHERS PHYSICS (HINGLISH) MECHANICAL PROPERTIES OF FLUIDS for Class 11
| Class 11 | PHYSICS |
| Chapter | MECHANICAL PROPERTIES OF FLUIDS |
| MODERN PUBLISHERS PHYSICS (HINGLISH) | Competition File (Assertion Reason Type Questions) |
| Medium | English |
| Academic Year | 2023-2024 |
Question 21
Two small spherical metal balls, having equal masses, are made from materials of densities ρ1andρ2(ρ1=8ρ2) and have radii 1 mm and 2mm respectively, they are made to fall vertically (from rest) in a viscous medium whose coefficient of viscosity equal η and whose density is 0.1 ρ2. The ratio of their terminal velocities would be View SolutionQuestion 22
A U-tube with both ends open to the atmosphere is partially filled with water. Oil, which is immiscible with water. Is poured into one side until it stands at a distance of 10mm above the water level on the other side. Meanwhile the water rises by 65mm from its original level (see diagram). The density of the oil is:
 View Solution
View SolutionQuestion 26
Two non-mixing liquids of densities ρ and (n>1) are put in a container. The height of each liquid is h. A solid cylinder of length L and density d is put in this container. The cylinder floats with its axis vertical and length pL(p<1) in the denser liquid. The density d is equal to : View SolutionQuestion 27
A ball is made of a material of density ρ where ρoil<ρ<ρwater with ρoil and ρwater representing the densities of oil and water, respectively. The oil and water are immiscible. If the above ball is in equilibrium in a mixture of this oil and water, which of the following pictures represents its equilibrium position?View SolutionQuestion 30
A small soap bubble of radius 4 cm is trapped inside another bubble of radius 6 cm without any contact. Let P2 be the pressure inside the inner bubble and P0, the pressure outside the outer bubble. Radius of another bubble with pressure difference P2−P0 between its inside and outside would be : View SolutionQuestion 33
Assume that a drop of liquid evaporates by decreases in its surface energy, so that its temperature remains unchanged. What should be the minimum radius of the drop for this to be possible? The surface tension is T, density of liquid is ρ and L is its latent heat of vaporization.View SolutionQuestion 34
A uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring such that it is half submerged in a liquid of density σ at equilibrium position. The extension x0 of the spring when it is in equlibrium is:View SolutionQuestion 36
An open glass tube is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46 cm. what will be length of the air column above mercury in the above now ?
(Atmospheric pressure = 76 cm of Hg)View SolutionQuestion 37
On heating water, bubbles being formed at the bottom of the vessel detach and rise. Take the bubbles to be spheres of radius R and making a circular contact of radius r with the bottom of the vessel. If r<<R and the surface tension of water is T, value of r just before bubbles detach is: (density of water is ρw)
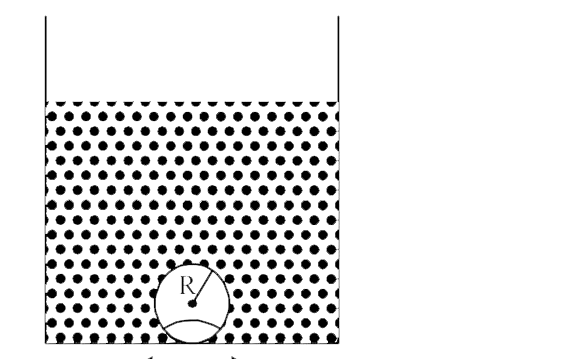 View Solution
View SolutionQuestion 39
A tank with a small hole at the bottom has been filled with water and kerosene (specific gravity 0.8). The height of water is 3 m and that of kerosene 2 m. When the hole is opened the velocity of fluid coming out from it is nearly: (take g = 10 ms−2 and density of water =103 kg m−3)View SolutionQuestion 46
If two glass plates have water between them and are separated by very small distance (see figure). It is very difficult to pull them apart. It is because the water in between forms cylindrical surface on the side that gives rise ot lower pressure in the water in comparison to atmosphere. If the radius of the cylindrical surface is R and surface tension of water is T then the pressure in water between the plates is lowr by: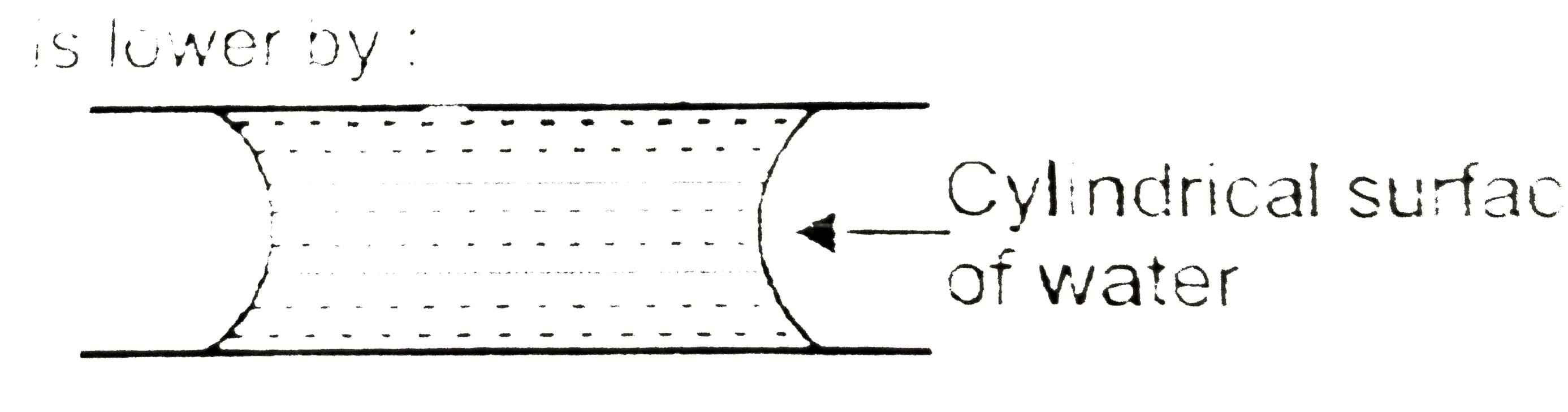 View Solution
View SolutionQuestion 47
_E01_261_Q01.png)
Consider a water jar of radius R that has water filled up to height H and is kept on a stand of height h (see figure) through a hole of radius r(r<<R) at its bottom the water leaks out and the stream of water coming down towards the ground has a shape like a funnel as shown in the figure. it the radius of the cross-section of water stream when it hits the ground is x. then.View SolutionQuestion 48
A wooden block floating in a bucket of water has 4/5 of its volume submerged. When certain amount of an oil is poured into the bucket, it is found that the block is just under the oil surface with half of its volume under water and half in oil. The density of oil relative to that of water is:View SolutionQuestion 49
The ratio of surface tensions of mercury and water is given to be 7.5 while the ratio of their densities is 13.6. Their contact angles, with glass, are close to 135° and 0°, respectively. It is observed that mercury gets depressed by an amount h in a capillary tube of radius r1 while water rises the same amount h in a capillary tube of radius r2. The ratio, (r1/r2) , is then close toView SolutionQuestion 50
When liquid medicine of density ρ is to put in the eye, it is done with the help of a dropper. As the bulp on the top of the dropper is pressed, a drop forms at the opening of the dropper. We wish to estimate the size of the drop. We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy. To determine the size, we calculate the net vertical force due to the surface tension T when the radius of the drop is R. When this force becomes smaller than the weight of the drop, the drop gets detached from the dropper.
If the radius of the opening of the dropper is r, the vertical force due to the surface tension on the drop of radius R (assuming r ltltR) is View SolutionQuestion 51
When liquid medicine of density ρ is to be put in the eye, it is done with the help of a dropper. As the bylb on the top of the dropper is pressed. A drop frons at the opening of the dropper. We wish to estimate the size of the drop.
We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy, To determine the size. We calculate the net vertical force due to the surface tension T when the radius of the drop is R. when this force become smaller than the weight of the drop the drop gets detached from the dropper.
If r=5×10−4m,ρ=103kgm−3,g=10ms−2,T=0.11Nm−1, The radius of the drop when it detaches from the dropper is approximately,View SolutionQuestion 52
When liquid medicine of density ρ is to be put in the eye, it is done with the help of a dropper. As the bylb on the top of the dropper is pressed. A drop frons at the opening of the dropper. We wish to estimate the size of the drop.
We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy, To determine the size. We calculate the net vertical force due to the surface tension T=0.11 when the radius of the drop is R=1.4mm. when this force become smaller than the weight of the drop the drop gets detached from the dropper.
After the drop detaches, its surface energy is View SolutionQuestion 53
Water is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)View SolutionQuestion 54
Water is filled up to a height h in a beaker of radiys R as shown in the figure. The density of water is ρ, the surface tension of water is T and the atmospheric pressure is P0. Consider a vertical section ABCD of the water column through a diameter of the beaker. The force on water on one side on this section by water on the other side of this section has magnitude
 View Solution
View SolutionQuestion 55
Two soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2. The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap. Water used to make bubbles is 0.04N/m. Find the ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B respectively. [Neglect the effect of gravity.]View SolutionQuestion 56
A cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice.
[Take atmospheric pressure =1.0×105N/m2, density of water=1000kg//m^3andg=10m//s^2. Neglect any effect of surface tension.]View SolutionQuestion 57
A glass tube of uniform internal radius (r) has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble of radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve.
 View Solution
View SolutionQuestion 58
A spherical solid ball of volume V is made of a material of density ρ1. It is falling through a liquid of density ρ2(ρ2<ρ1). Assume that the liquid applies a viscous force on the ball that is proportional to the square of its speed v, i.e., Fviscous=−kv2(k>0). The terminal speed of the ball is View SolutionQuestion 63
A glass capillary tube is of the shape of a truncated cone with an apex angle α so that its two ends have cross sections of different radii. When dipped in water vertically, water rises in it to a high h, where the radius of its cross section is b. If the surface tension of water is S, its density if ρ, and its contact angle with glass is θ, the value of h will be (g is the acceleration due to gravity)
 View Solution
View SolutionQuestion 65
A uniform capillary tube of inner radius r is dipped vertically into a beaker filled with water. The water rises to a height h in the capillary tube above the water surface in the beaker. The surface tension of water is σ. The angle of contact between water and the wall of the capillary tube is θ. Ignore the mass of water in the meniscus. Which of the following statements is (are) true? View SolutionQuestion 67
Two solid spheres A and B of equal volumes but of different densities dAanddB are connected by a string. They are fully immersed in a fluid of density dF. They get arranged into an equilibrium state as shown in the figure with a tension in the string. The arrangement is possible only if
 View Solution
View SolutionQuestion 72
A small tank of cylindrical shape and of radius R is containing a liquid of density σ. On rotating the vessel about its axis with angular velocity ω, the liquid rises at the sides of vessel through height h. P1andP2 are pressure at sides and at the centre of tank respectively, thenView SolutionQuestion 74
Two spheres P and Q of equal radii have densities ρ1 and ρ2, respectively. The spheres are connected by a massless string and placed in liquids L1 and L2 of densities σ1 and σ2 and viscosities η1 and η2, respectively. They float in equilibrium with the sphere P in L1 and sphere Q in L2 and the string being taut(see figure). If sphere P alone in L2 has terminal velocity →Vp and Q alone in L1 has terminal velocity →VQ, then
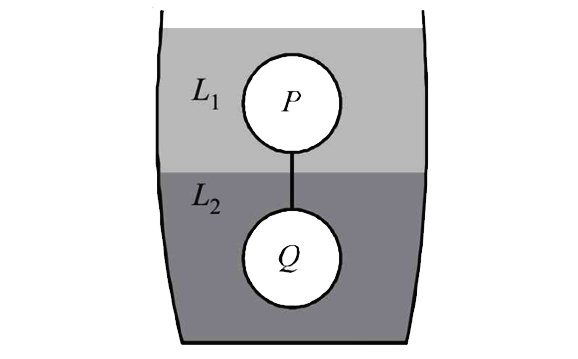 View Solution
View SolutionQuestion 75
A solid sphere of radius R and density ρ is attached to one end of a mass-less spring of force constant k. The other end of the spring is connected to another solid sphere of radius R and density 3ρ. The complete arrangement is placed in a liquid of density 2ρ and is allowed to reach equilibrium. The correct statements(s) is (are)View SolutionQuestion 76
When a liquid moves steadily under some pressure through a horizontal tube, it moves in the form of cylindrical layers coaxial to the ends of the tube. The velocity of different layers is different. The velocity of the layer is maximum along the axis of the tube and it decreases as one moves towards the walls of the tube. According to Poiseuille, the rate of flow of liquid through a horizontal capillary tube varies as the relation Vαpr4ηl where l and r are the length and radius of the tube and p is the pressure different between the ends of the tube and is the constant of proportionality.
The dimensional formula for rate of flowView SolutionQuestion 77
When a liquid moves steadily under some pressure through a horizontal tube, it moves in the form of cylindrical layers coaxial to the ends of the tube. The velocity of different layers is different. The velocity of the layer is maximum along the axis of the tube and it decreases as one moves towards the walls of the tube. According to Poiseuille, the rate of flow of liquid through a horizontal capillary tube varies as the relation Vαpr4ηl where l and r are the length and radius of the tube and p is the pressure different between the ends of the tube and is the constant of proportionality.
πpr48ηl is dimensionally equivalent to (R is the resistance)View SolutionQuestion 78
When a liquid moves steadily under some pressure through a horizontal tube, it moves in the form of cylindrical layers coaxial to the ends of the tube. The velocity of different layers is different. The velocity of the layer is maximum along the axis of the tube and it decreases as one moves towards the walls of the tube. According to Poiseuille, the rate of flow of liquid through a horizontal capillary tube varies as the relation Vαpr4ηl where l and r are the length and radius of the tube and p is the pressure different between the ends of the tube and is the constant of proportionality.
When two capillary tubes through which the liquid is flowing are joined in series then the equivalent liquid resistance isView SolutionQuestion 79
When a liquid moves steadily under come pressure through a horizontal tube, it moves in the form of cylindrical layers coaxial to the exds of the tube. The velocity of different layers is different. The velocity of the layer is maximum along the axis of the tube and it decreases as one moves towards the walls of the tube. According to Poiseuille, the rate of flow of liquid through a horizontal capillary tube varies as the relation Vαpr4ηl where l and rare the length and radius of the tube and p is the pressure different between the ends of the tube and is the constant of proportionality.
Which of the following is correct: View SolutionQuestion 80
Streamline flow of the liquid is the flow in which every particle of the liquid follows the same path as the path of the preceeding particle and has the same velocity as that of the preeding particle while crossing through the same points. Two streamlines can never cut each other. When a liqui moves randomly or in irregular manner such that its velocity becomes greater than the critical velocity than the flow is turbulent flow. Critical velocity is given by vc=Kηpr.
For liquids having Reynold number greater than 3000 the flow is View SolutionQuestion 81
Streamline flow of the liquid is the flow in which every particle of the liquid follows the same path as the path of the preceeding particle and has the same velocity as that of the preeding particle while crossing through the same points. Two streamlines can never cut each other. When a liqui moves randomly or in irregular manner such that its velocity becomes greater than the critical velocity than the flow is turbulent flow. Critical velocity is given by vc=Kηpr.
For flow to be streamlined theView SolutionQuestion 82
Streamline flow of the liquid is the flow in which every particle of the liquid follows the same path as the path of the preceeding particle and has the same velocity as that of the preeding particle while crossing through the same points. Two streamlines can never cut each other. When a liqui moves randomly or in irregular manner such that its velocity becomes greater than the critical velocity than the flow is turbulent flow. Critical velocity is given by vc=Kηpr.
Which of the following is incorrect?View SolutionQuestion 83
Streamline flow of the liquid is the flow in which every particle of the liquid follows the same path as the path of the preceeding particle and has the same velocity as that of the preeding particle while crossing through the same points. Two streamlines can never cut each other. When a liqui moves randomly or in irregular manner such that its velocity becomes greater than the critical velocity than the flow is turbulent flow. Critical velocity is given by vc=Kηpr.
The viscosity of water is 0.0013 Nsm^(−2). The maximum velocity of water in a tube of diameter 0.3 cm for the flow to be laminar isView SolutionQuestion 84
A wooden cylinder of diameter 4r height H and density pdet<a is kept on a hole of diameter 2r of a tank filled with water of density as shown in the figure. If level of liquid starts decreasing slowly when the level of liquid is at a height h1 above the cylinder the block just starts moving up. Then value of h1 is: View Solution
View SolutionQuestion 87
A spray gun is shown in the figure where a piston pushes air out of a nozzle. A thin tube of uniform cross section is connected to the nozzle. The other end of the tube is in a small liquid container. As the piston pushes air through the nozzle, the liquid from the container rises into the nozzle and is sprayed out. For the spray gun shown, the radii of the piston and the nozzle are 20mm and 1mm respectively. The upper end of the container is open to the atmosphere.

If the piston is pushed at a speed of 5mms−1, the air comes out of the nozzle with a speed of View SolutionQuestion 88
A spray gun is shown in the figure where a piston pushes air out of a nozzle. A thin tube of uniform cross section is connected to the nozzle. The other end of the tube is in a small liquid container. As the piston pushes air through the nozzle, the liquid from the container rises into the nozzle and is sprayed out. For the spray gun shown, the radii of the piston and the nozzle are 20mm and 1mm respectively. The upper end of the container is open to the atmosphere.

If the piston is pushed at a speed of 5mms−1, the air comes out of the nozzle with a speed of View SolutionQuestion 89
A small spherical monoatomic ideal gas bubble (γ=5/3) is trapped inside a liquid of density p1 (see figure). Assume that bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0. Height of the liquid is H and atmospheric pressure is P0. -Neglect surface tension.
As the bubble moves upwards, besides the buoyancy force the following forces are acting on it.View SolutionQuestion 90
A small spherical monoatomic ideal gas bubble (γ=5/3) is trapped inside a liquid of density ρ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure P0 (Neglect surface tension).

When the gas bubble is at a height y from the bottom, its temperature is-View SolutionQuestion 91
A small spherical monoatomic ideal gas bubble (γ=5/3) is trapped inside a liquid of density ρ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure P0 (Neglect surface tension).

When the gas bubble is at a height y from the bottom, its temperature is-View SolutionQuestion 102
Statement-1 : The stream of water flowing at high speed from a garden hose pipe tends to spread like a foundtion when held vertically up, but tends to narrow down when held vertically down.
Statement-2 : In any steady flow of an incompressible fluid, the volume flow rate of the fluid remain constant.View SolutionQuestion 109
In a capillary tube, liquid rises to a height of 4 cm. In the same capillary tube, mercury falls to a depth of 3 cm. The density of liquid and mercury are 1.5 g/cc and 13.6 g/cc. Then angles of contact of liquid and mercury with the same capillary tubes are 0∘and140∘, respectively. What is the ratio of magnitudes of approximate surface tension of mercury and the liquid?View SolutionQuestion 111
The cross sectional area of a horizontal pipe is decreasing from 5×10−2m2 to 1×10−2m2?. Water is flowing with speed of 5 m/s through this pipe with a pressure of 5×105Pa through the larger cross section. The pressure at the smaller cross section of the pipe is n×104Pa. Find the value of n. View SolutionQuestion 115
Consider two solid spheres P and Q each of density 8gmcm−3 and diameters 1cm and 0.5cm, respectively. Sphere P is dropped into a liquid of density 0.8gmcm−3 and viscosity η=3 poiseulles. Sphere Q is dropped into a liquid of density 1.6gmcm−3 and viscosity η=2 poiseulles. The ratio of the terminal velocities of P and Q isView Solution
All Exercises from MODERN PUBLISHERS PHYSICS (HINGLISH) Class 11 PHYSICS MECHANICAL PROPERTIES OF FLUIDS
- PRACTICE PROBLEMS
- CONCEPTUAL QUESTIONS
- PROBLEMS
- NCERT (ADDITIONAL EXERCISES)
- NCERT (EXEMPLAR PROBLEMS (SUBJECTIVE QUESTIONS))
- NCERT (SHORT ANSWER TYPE QUESTIONS)
- NCERT (TEXTBOOK EXERCISES)
- NCERT FILE (EXEMPLAR PROBLEMS (OBJECTIVE QUESTIONS))
- NCERT FILE (MCQ)
- HOTS (HIGHER ORDER THINKING SKILLS) (ADVANCED LEVEL))
- REVISION EXERCISE (ADDITIONAL QUESTIONS)
- REVISION EXERCISE (FILL IN THE BLANKS)
- REVISION EXERCISE (LONG ANSWER QUESTIONS)
- REVISION EXERCISE (NUMERICAL PROBLEMS)
- REVISION EXERCISE (SHORT ANSWER QUESTIONS)
- REVISION EXERCISE (VERY SHORT ANSWER QUESTIONS)
- COMPETITION FILE (A. MCQ (OBJECTIE TYPE QUESTIONS))
- COMPETITION FILE (ASSERTION REASON TYPE QUESTIONS)
- COMPETITION FILE (B. MCQ (AIPMT/NEET & OTHER STATE BOARDS FOR MEDICAL ENTRANCE))
- COMPETITION FILE (C. MCQ WITH MORE THAN ONE CORRECT ANSWERS)
- COMPETITION FILE (D. MCQ BASED ON A GIVEN PASSAGE/COMPREHENSION)
- COMPETITION FILE (INTEGERS TYPE QUESTIONS)
- COMPETITION FILE (JEE (ADVANCED) FOR IIT ENTRANCE)
- COMPETITION FILE (JEE (MAIN) & OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)
- COMPETITION FILE (MATCHING TYPE QUESTIONS )
- CHAPTER PRACTISE TEST
- SOLVED EXAMPLES







