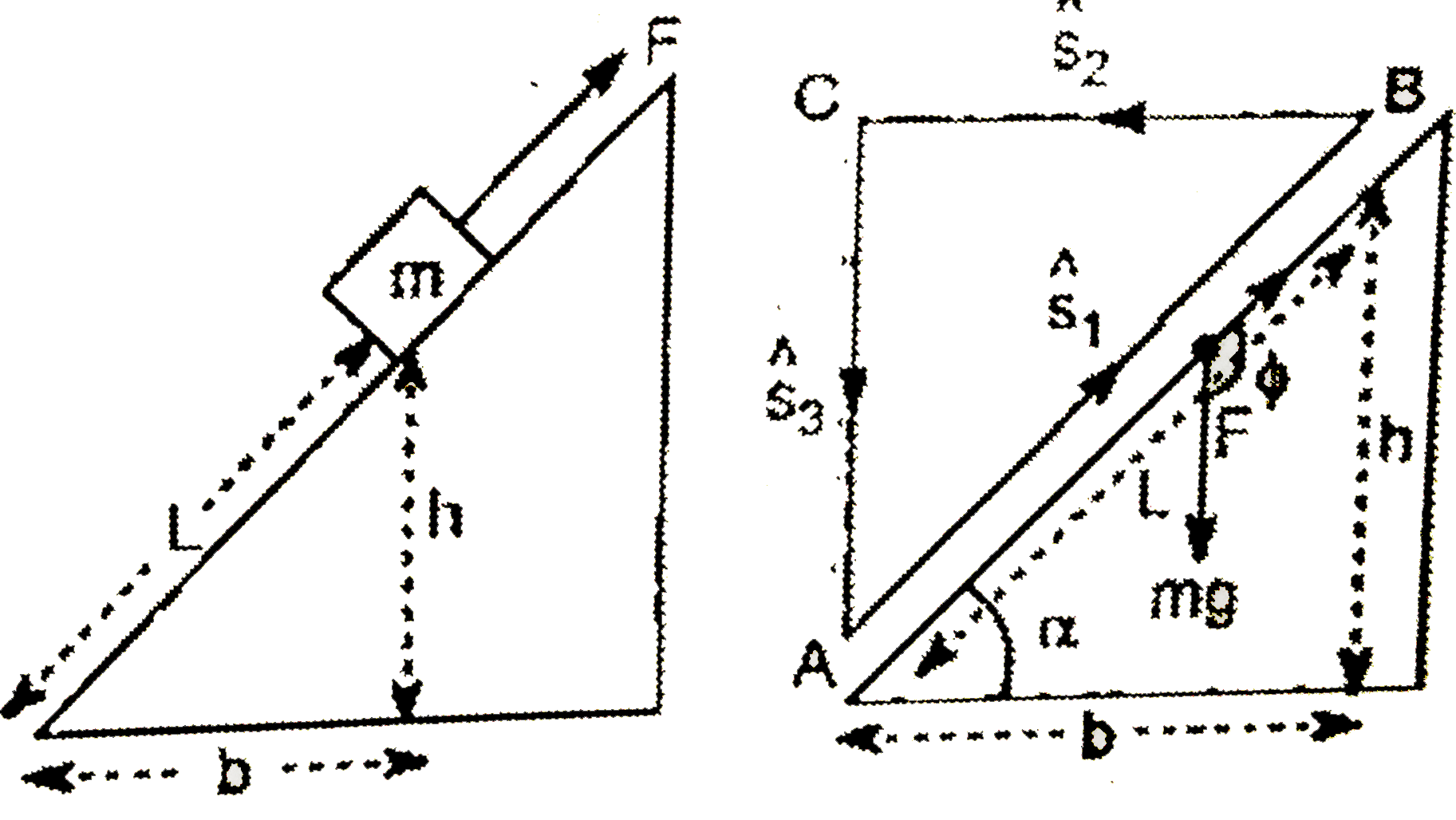Eample from SHREE BALAJI PHYSICS (HINGLISH) WORK AND ENERGY for Class 11
| Class 11 | PHYSICS |
| Chapter | WORK AND ENERGY |
| SHREE BALAJI PHYSICS (HINGLISH) | Eample |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
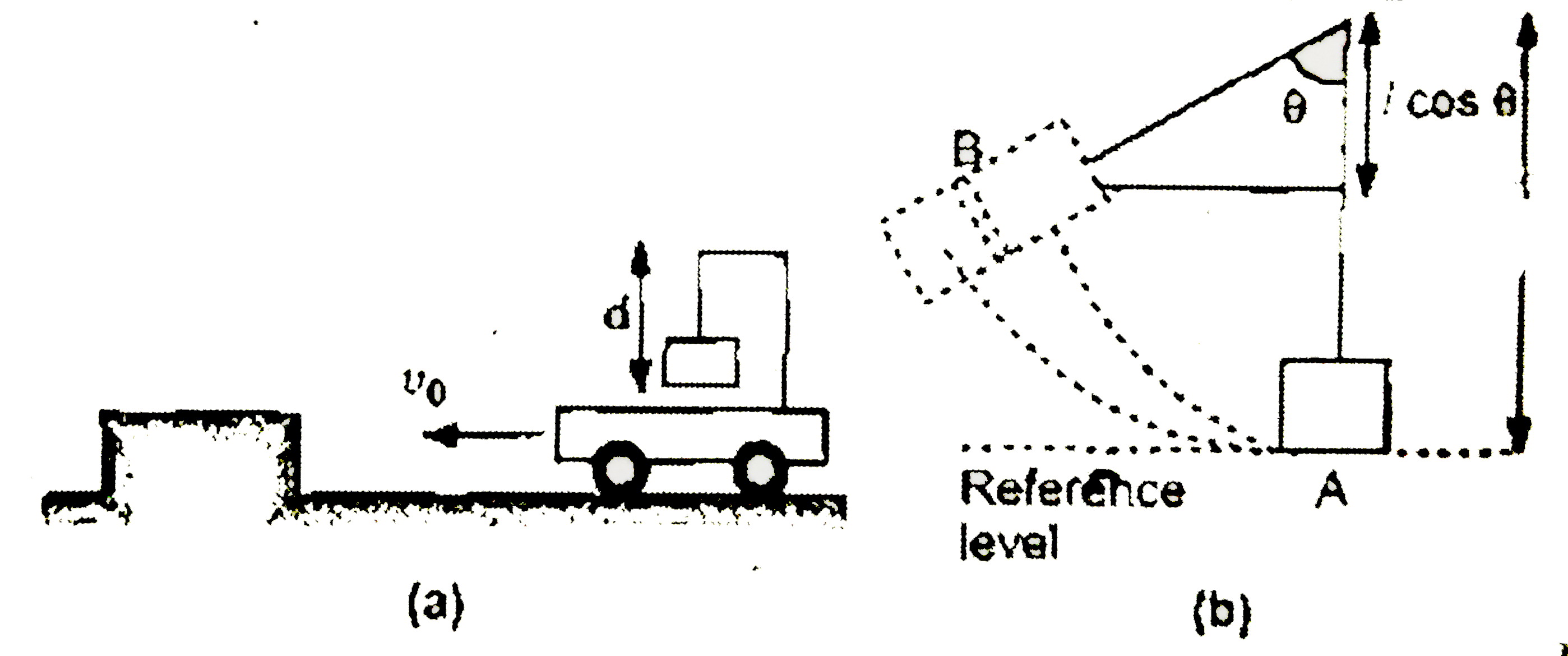
A plank of mass M and length L is placed at rest on a smooth horizontal surface A small block of mass m is projected wii:h a velocity v0 as shown in the Fig. 3.31 (a), The coefficient of friction between the block and the plank is μ, plank is very long so that block eventually comes to rest on it.
(i) Find the work done by the ftjctioh force on the block during the period it slides on the plank. Is the Work positive or negative ?'
(ii) Calculate the work done on the plank during the same period. Is the work positive or negative?
(iii) Also, determine the net work done by friction. Is it positive or negative ?
 View Solution
View SolutionQuestion 8
A spring block system is placed on a rough horizontal surface having coefficient of friciton μ. The spring is given initial elongation 3μmg/k (where m=mass of block and k=spring constant) and the block is released from rest. For the subsequent motion, find
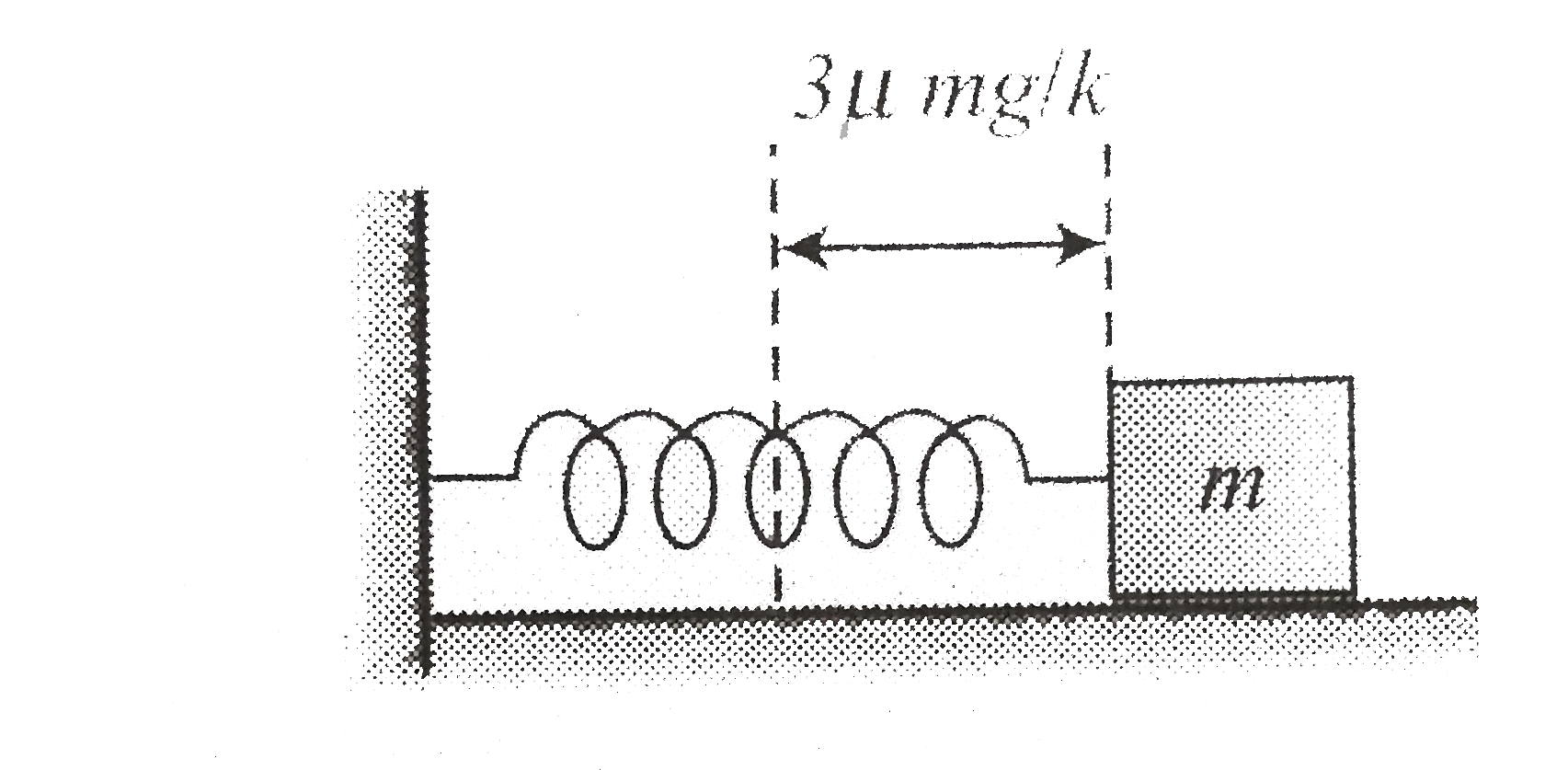
a. Initial acceleration of block
b. Maximum compression in spring
c. Maximum speed of the blockView SolutionQuestion 9
In the figure shown, the mass of the hanging block is m, while that of the black resting on the floor is 3m. The floor is horizontal and frictionless and all pulleys ideal. The system is initially held stationary with the inclined thread making an angle θ=30∘ with the horizontal. The blocks are now released from rest and allowed to move. the hanging block falls through a height (49.5) m before hitting the floor. it is found that the value of θ becomes 60∘, when the hanging block hits the floor. Find the speed with which the hanging block hits the floor.
 View Solution
View SolutionQuestion 10
Two blocks having masses 8kg and 16 kg are connected to the two ends of a light spring. The system is placed on a smooth horizontal floor. An inextensible starting also connects B with ceiling as shown in figure at the initial moment. Initially the spring has its natural length. A constant horizontal force F is applied to the heavier block as shown. What is the maximum possible value of F so the lighter block doesn't loose contant with ground
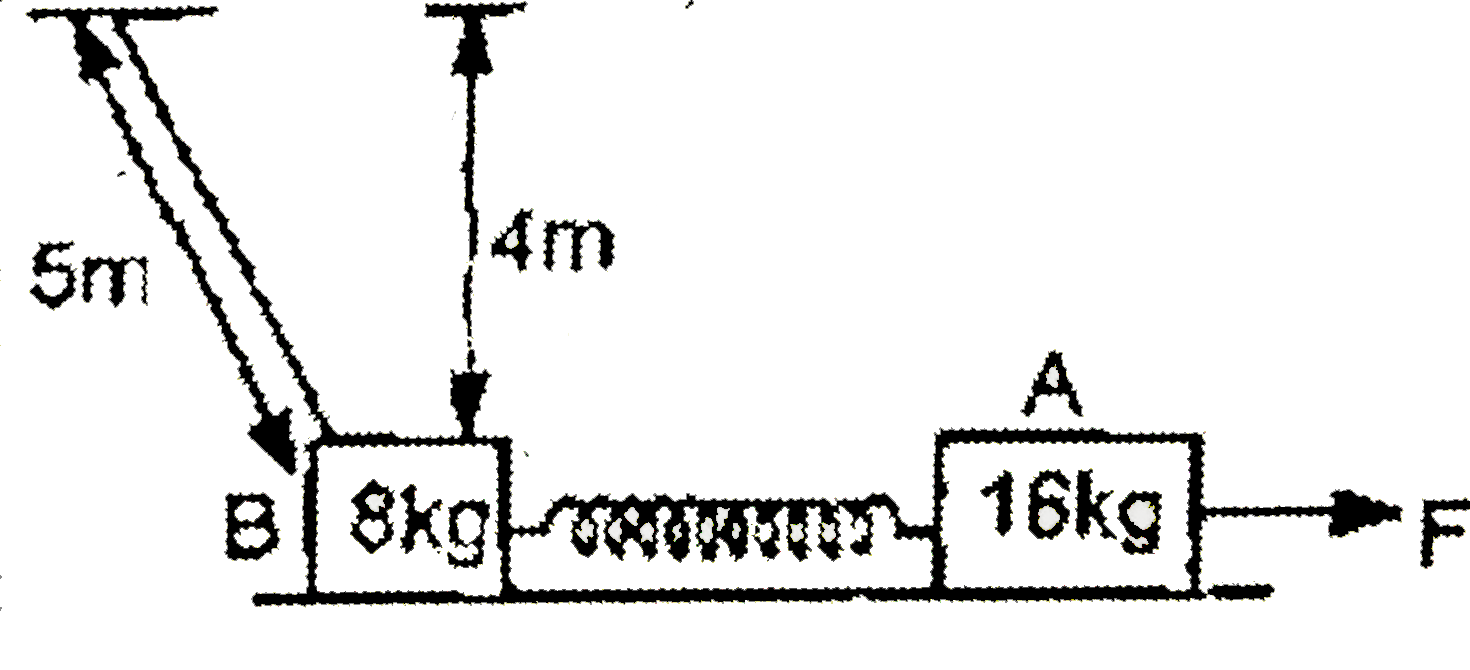 View Solution
View SolutionQuestion 11
a. A 2−kg situated on a smooth fixed incline is connected to a spring of negligible mass, with spring constant k=100Nm−1, via a frictionless pulley. The block is released from rest when the spring is unstretched. How far does the block moves down the incline before coming (momentarily) to rest? What is its acceleration at its lower point?
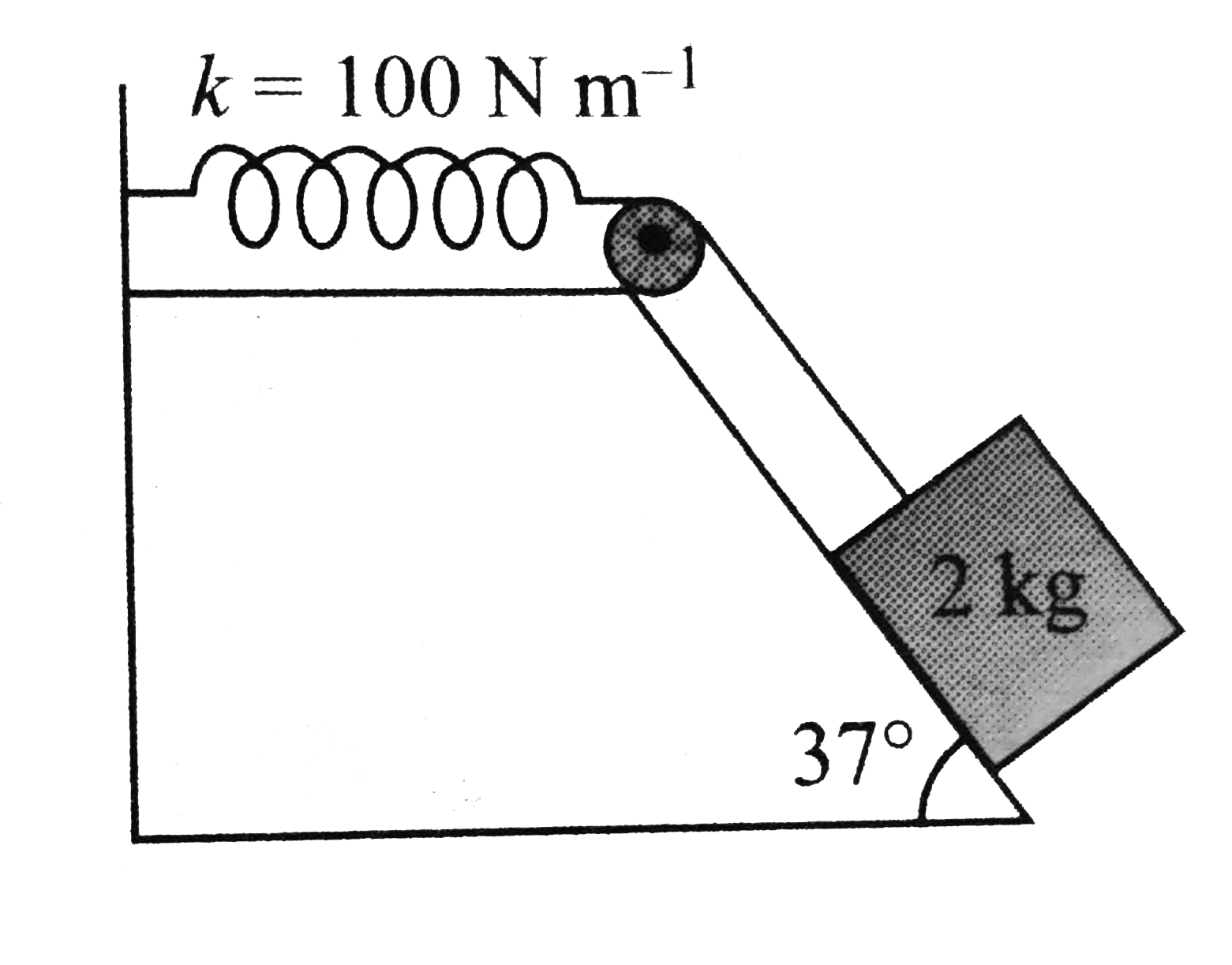
b. The experiment is repeated on a rough incline. If the block is observed to move 0.20m down along the incline before it comes to instantaneous rest, calculate the coefficient of kinetic friction.View SolutionQuestion 12
A ring of mass m=1kg can slide over a smooth vertical rod. A light string attached to the ring passing over a smooth fixed pulley at a distance of L=0.7m from the rod as shown in figure.
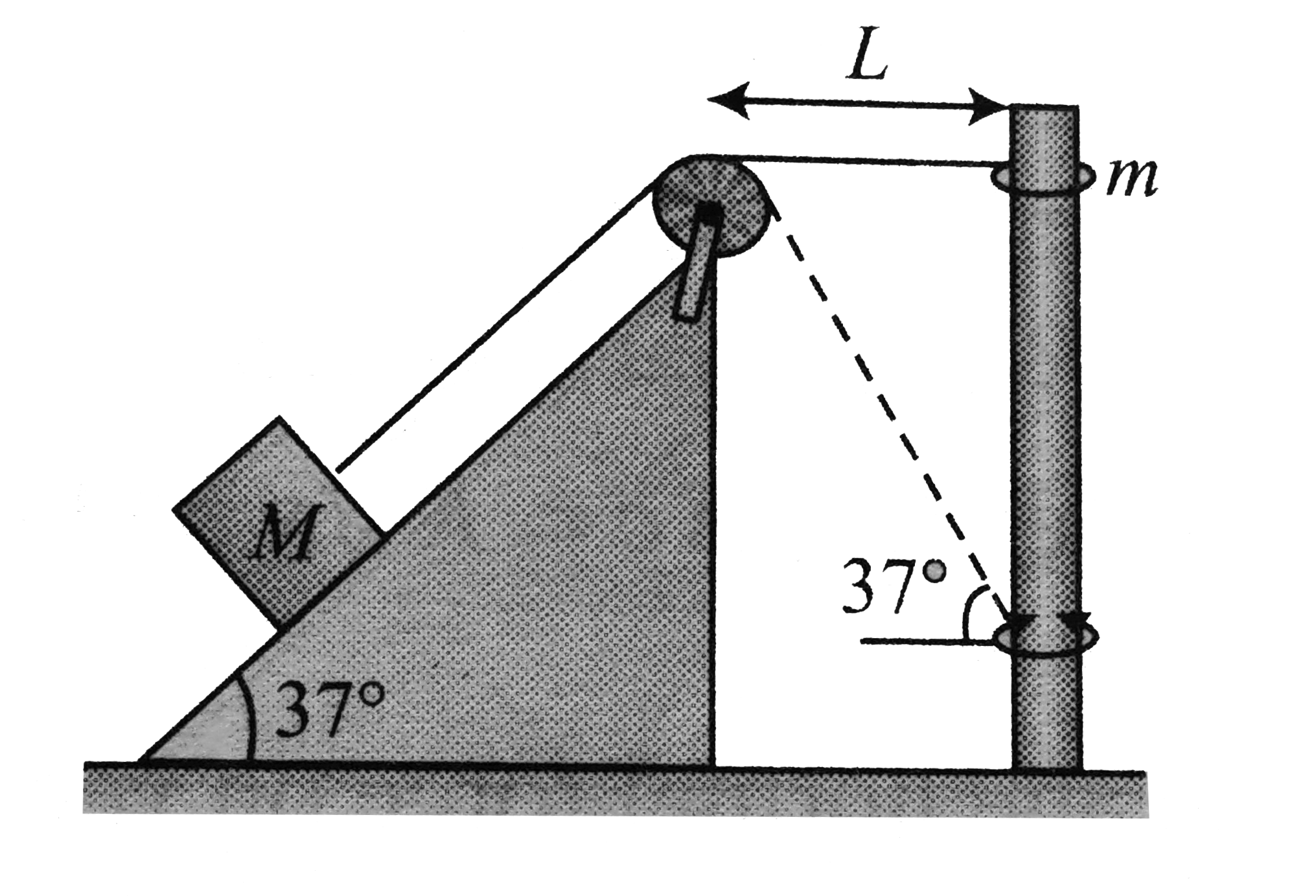
At the other end of the string mass M=5kg is attached, lying over a smooth fixed inclined plane of inclination angle 37∘. The ring is held in level with the pulley and released. Determine the velocity of ring when the string makes an angle (α=37∘) with the horizontal. [sin37∘=0.6]View SolutionQuestion 18
In Fig 3E.17, the mass m2 rests on a rough table. The mass m1 is pushed against the spring to which it is not attached Force constant of the spring is k, coefficient of friction is μk.
(a) Find the speed of the blocks after the spring is released and m2 has fallen a distance of h.
(b) If the spring is attached to the block and it falls a distance h before coming to rest, calculate the coefficient of friction μk.
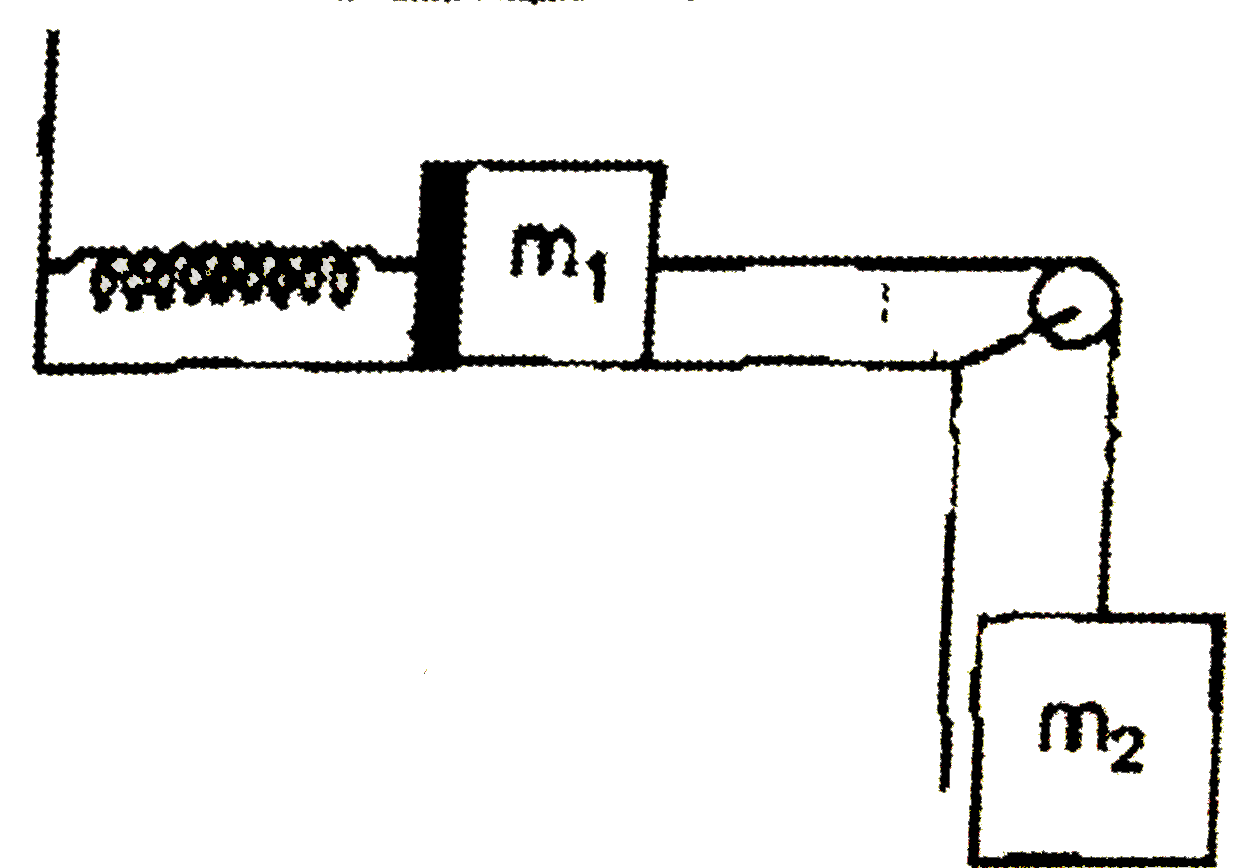 View Solution
View SolutionQuestion 26
A chain of mass m and length 1 lies on a rough table. The chain just starts to slip when the overhaning part equals nth fraction of the chain length. If the chain is slightly distributed so that it completely slips off the table, what is the work performed by the friction forces.
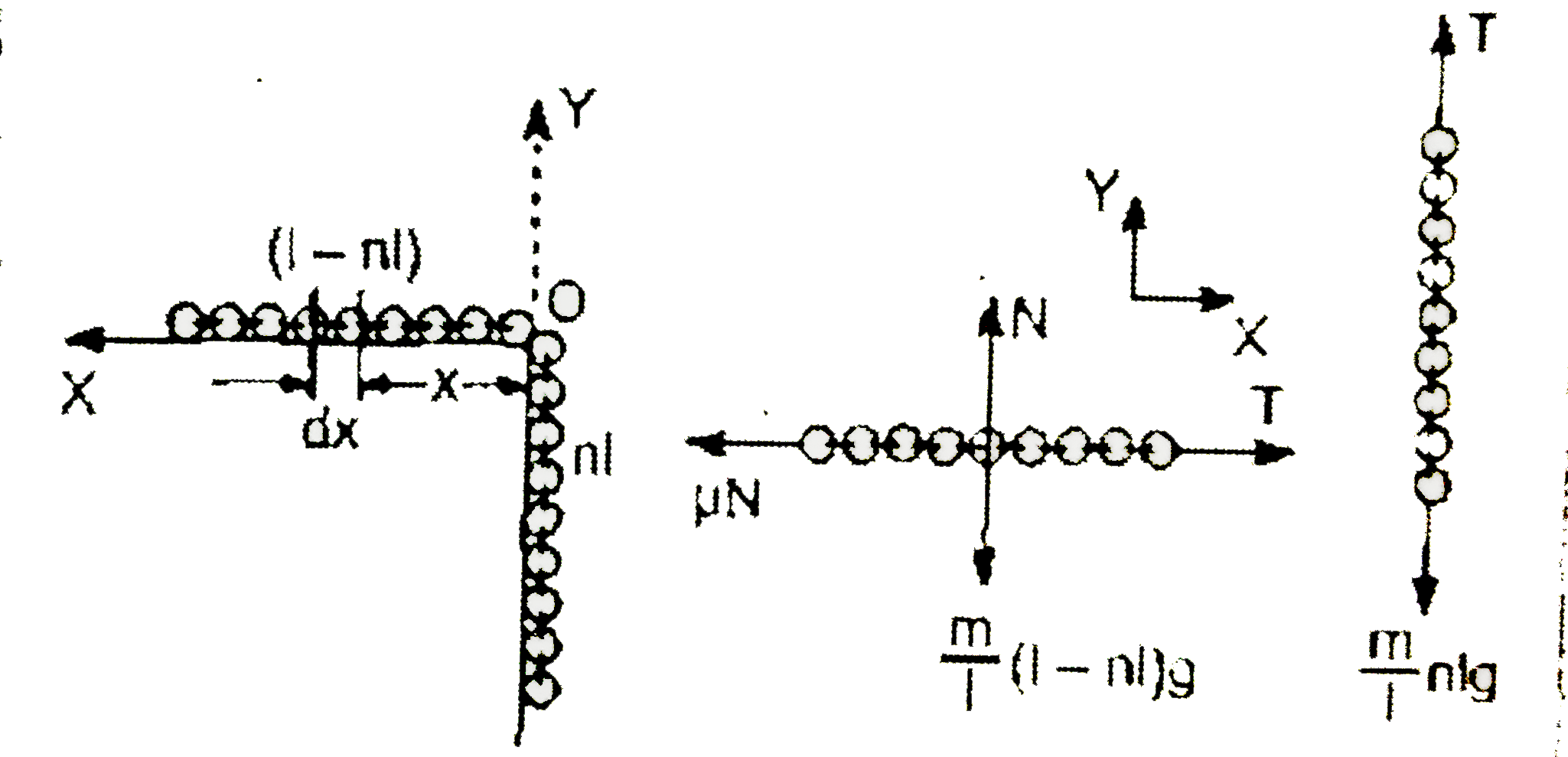 View Solution
View SolutionQuestion 29
A uniform chain of mass m and length l<πR2 is placed on a smooth hemisphere of radius R with on of its ends fixed at the top of the sphere.
(a) Find the gravitational potential energy of chain assuming base of hemisphere as reference.
(b) what will be the tangential acceleraion of the chain when it starts sliding down.
(c ) If the chain slides down the sphere, find the kinetic energy of the chain when it has slipped through an angle β.View SolutionQuestion 31
A pendulum bob can swing along a ciircular path on a smooth inclined plane, as shown in Fig. 3E.31, where m=1.2kg,1=.075m,θ=37∘. At the lowest point of the circle the tension in the sting is T=110N. Determine
(a) the speed of the bob at the lowest point,
(b) the speed of the bob at the highest point on the circle and
(c) the tension in the string at the highest position
(a)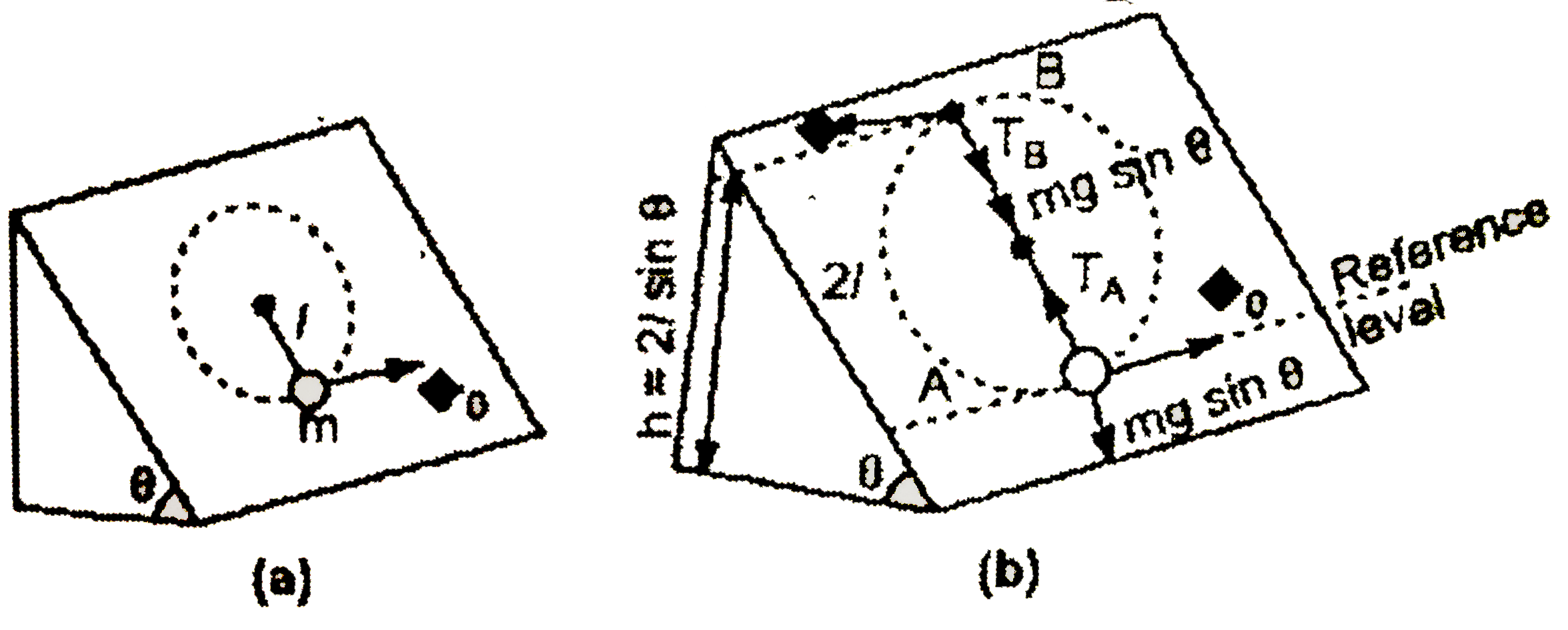 View Solution
View SolutionQuestion 32
A small toy car of mass m slides with negligible friction on a ''loop'' the loop track as shown in Fig.3E.32. The toy car starts from rest at a point H above the level of the lowest point of the track
(a) If H=2R, what normal force is exerted by the track on the toy car at point q?. What are the speed and normal force at point r ?
(b) At what height will the ball leave the track and to what maxiumum height will it rise afterwards ?
(c) If H=4R, what is the speed and normal reaction reaction at point s ?
 View Solution
View SolutionQuestion 33
A small ball is rolled with speed u from point A along a smooth circular track as shown in Fig. 3E.33. If x=3R, determine the required speed u so that the ball returns to A, the point of projection. What is the minimum value of x for which the ball can reach the point of projection ?
 View Solution
View SolutionQuestion 34
A block of mass m is pressed against a spring of force constant k. The block after leaving contact with the spring moves along a ''loop'' the loop track. The sliding surface is smooth except for rough portion of length s equal to R as shown in Fig. 3E.34, where the coefficient of friction is μk. Determine the minimum spring compression x for which the particle will not lose contant with the track ?
 View Solution
View SolutionQuestion 35
A particle attached to a vertical string of length 1m is projected horizontally with a velocity 5√2m/s
(a) What is maximum height reached by the particle from the lower most point of its trajectory.
(b) If the string breaks when it makes an angle of 60∘ with downward vertical, find maximum height reached by the particle from the lower most point of its trajectoryView SolutionQuestion 36
A particle is suspended by a light vertical inelastic string of length 1 from a fixed support. At its equilbrium position it is projected horizontally with a speed √6gl. Find the ratio of the tension in the string in its horizontal position to that in the string when the particle is vertically above the point of support.View SolutionQuestion 40
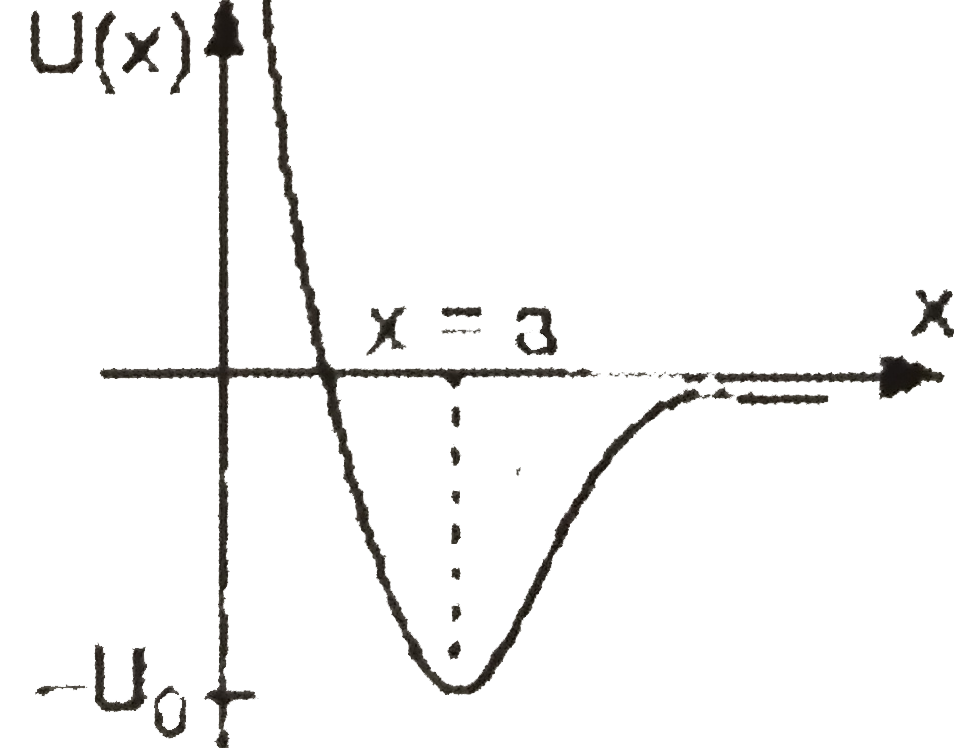
The force between two atoms in a diatomic molecule can be represented approaximately by the potential energy function
U=U0[(ax)12−2(ax)6]
where U0 and a are constant (a) At what value of x is the potential energy zero ?
(b) Fidn teh force Fx. (c) At what value of X is the potential energy a minmum ?
 View Solution
View SolutionQuestion 43
Consider a one-dimensional motion of a particle with total energy E. There are four regions A, B, C and D is which the relation between potential energy U, kinetic energy (K) and total energy E is as given below
RegionA:U>E Region B:U<E
Region C:K<E Region D:U>E
State with reason in each case whether a particle can be found in the given region or not.View SolutionQuestion 44
Two particle of mass m and 2m, connected by a massless rod, slide on the insider of a smooth circular ring of radius r, as shown in Fig. 3E.44 (a). If the assembly is released from rest when θ=0, determine
(a) the velocity of the particle when the rod passes the horizontal position,
(b) the maximum velocity vmax of the particles.
 View Solution
View SolutionQuestion 45
The figure shows a pendulum of length l suspended at a distance x vertically above a peg.
(a) The pendulum bob is deflected through an angle θ and then released. Find the speed of the bob at the instant
(b) The pendulum is released when θ=90∘. For what x (position of peg) will the pendulum complete the circle ?
(c) The pendulum is released when θ=60∘. what is the velocity of the bob as it passes position E.
 View Solution
View SolutionQuestion 46
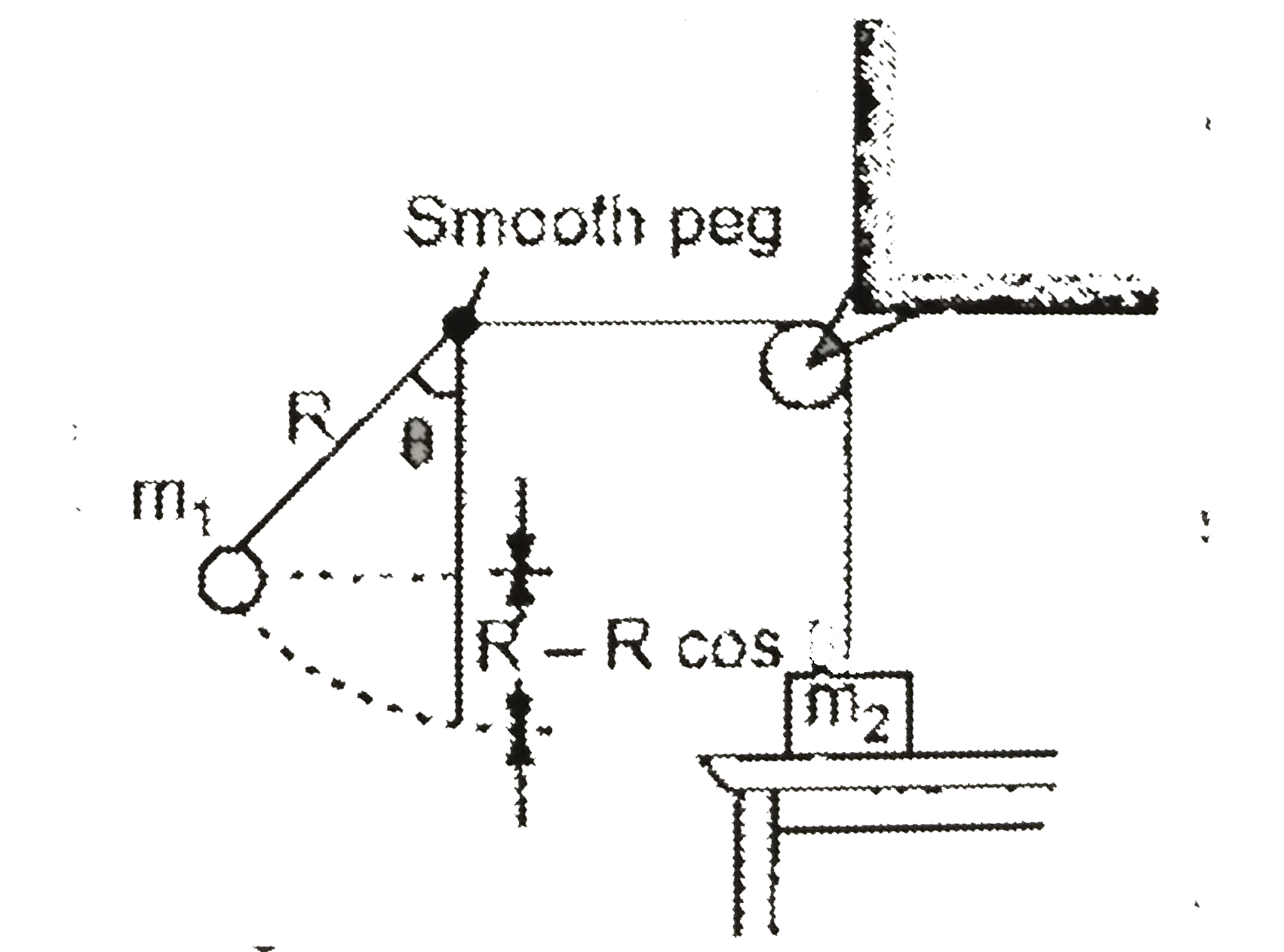
Two blocks are connected by a massless string that passes over a frictionless peg as shown in Fig. 3E.46. One end of the string is attached to a mass m1=3kg i.e. a distance R=1.20m from the peg. The other end of the string is connected to a block of mass m2=6kg resting on a table. From what angle θ, measured from the vertical, must the 3 kg block be released in order to just lift the 6 kg block off the table ?
 View Solution
View SolutionQuestion 47
Fig. 3E.47 (a) shows a circular ring of mass M that hangs in a vertical plane. Two beads of mass m are released simultaneously from the top of the ring in opposite directions. There is no frictional force between the bead and the ring. Show that the ring will starts to rise if m>3M2. If m = 2M, at what angle θ from vertical this happends ?
(a)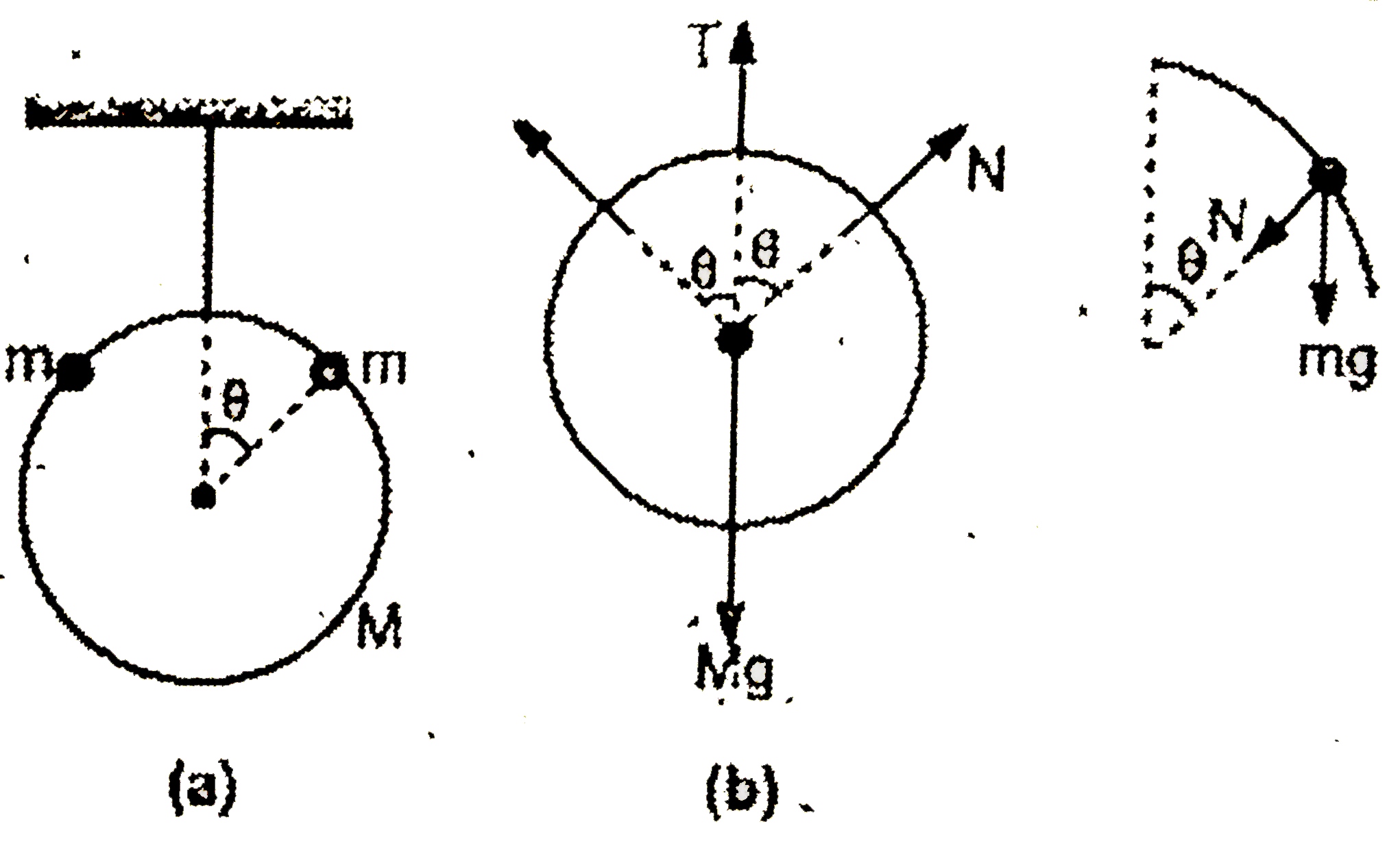 View Solution
View Solution