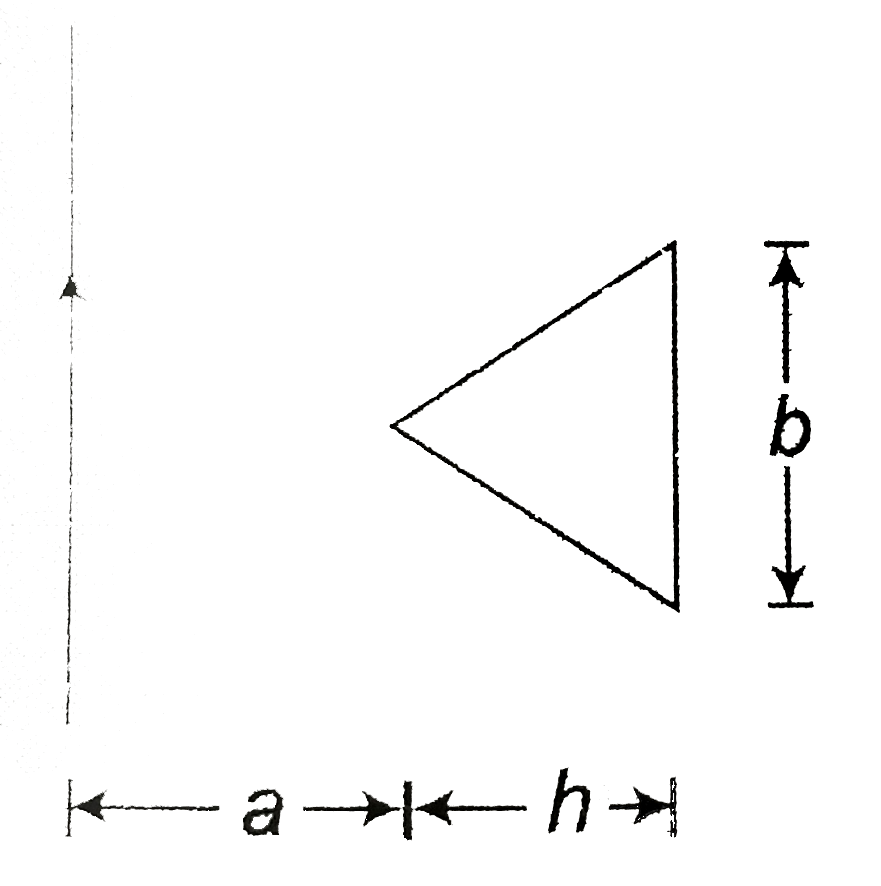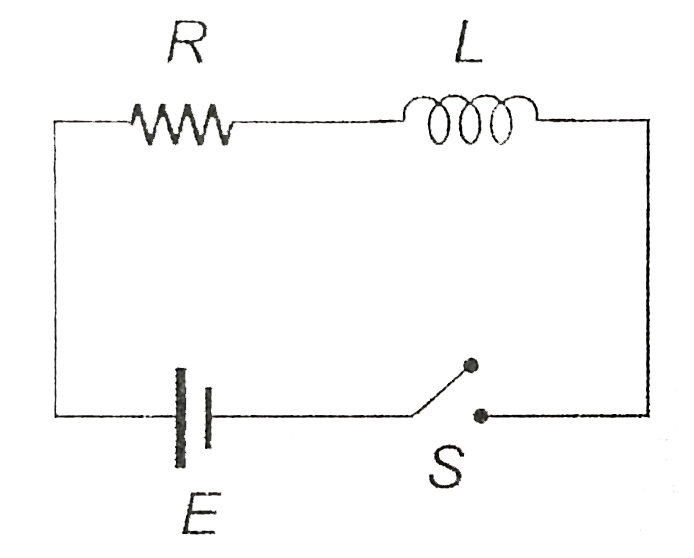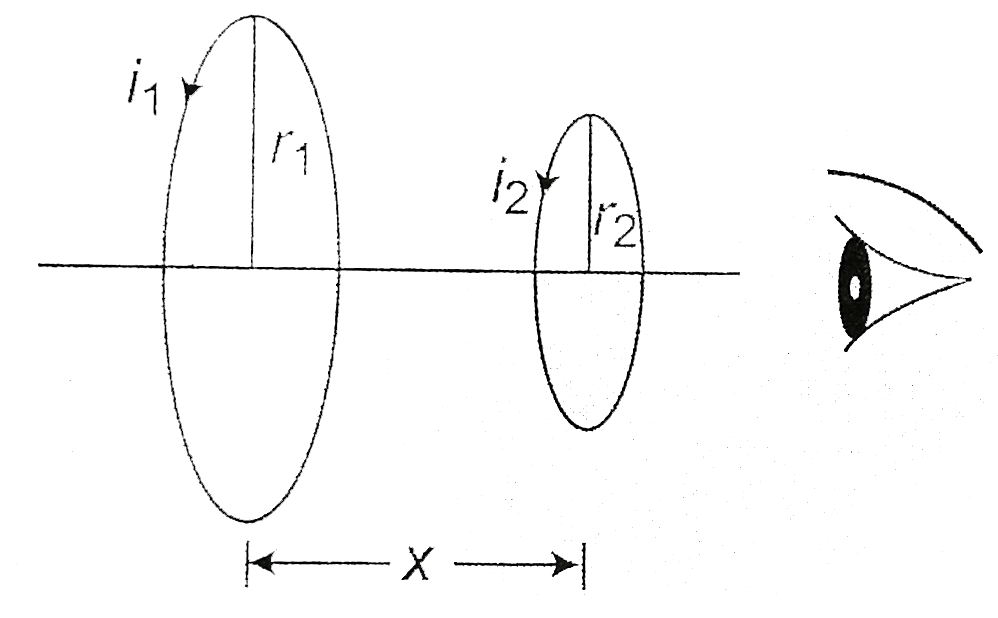EXAMPLE from CP SINGH PHYSICS Chapter 5 ELECTROMAGNETIC INDUCTION for Class 12
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETIC INDUCTION |
| CP SINGH PHYSICS | EXAMPLE |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
A long solenoid of radius 3cm , length I00cm carries a current of 4A . The total number of truns is 300 . Assuming ideal solenoid, find the flux passing through a circular surface having centre on axis of solenoid,
(a) of radius 2cm and is perprndicular of the axis of solenoid (i) inside and (ii) at the end of solenoid
(b) of radius 4cm and is perprndicular of the axis of solenoid
(c) of radius greater than 3cm and angle between normal to area and axis of solenoid is 60∘C View SolutionQuestion 2
The magnetic flux passing prependicular to the plane of the coil directed into the paper is varying according to the relation
ϕ=6t2+8t+I0 , where ϕ is in weber and t in second.
(a) What is the magnitude of emf induced in the loop when t=2sec ?
(b) What is the magnitude and direction of current at t=2sec ?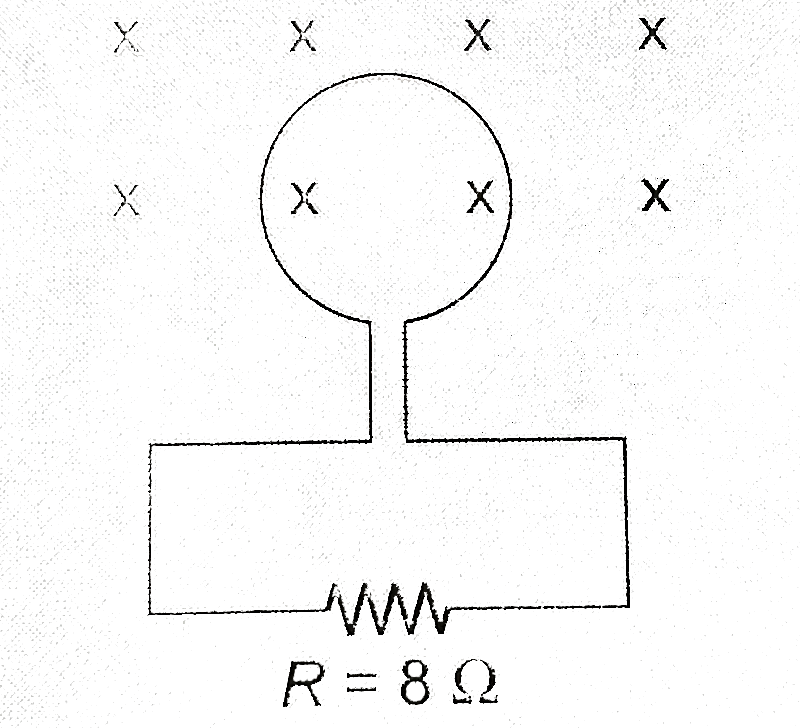 View Solution
View SolutionQuestion 6
A coil of area A lies in a uniform magnetic field B with its plane perpednicular to the field. In this position the normal to the coil makes an angle 0∘ with a field. The coil rotates at a uniform rate about its diameter to complete one rotation in time T . Find the average induced e.m.f. in the coil during the interval when coil rotates from:
(a) 0∘ to 90∘
(b) 90∘ to I80∘
(c) I80∘ to 270∘
(d) 270∘ to 360∘ View SolutionQuestion 8
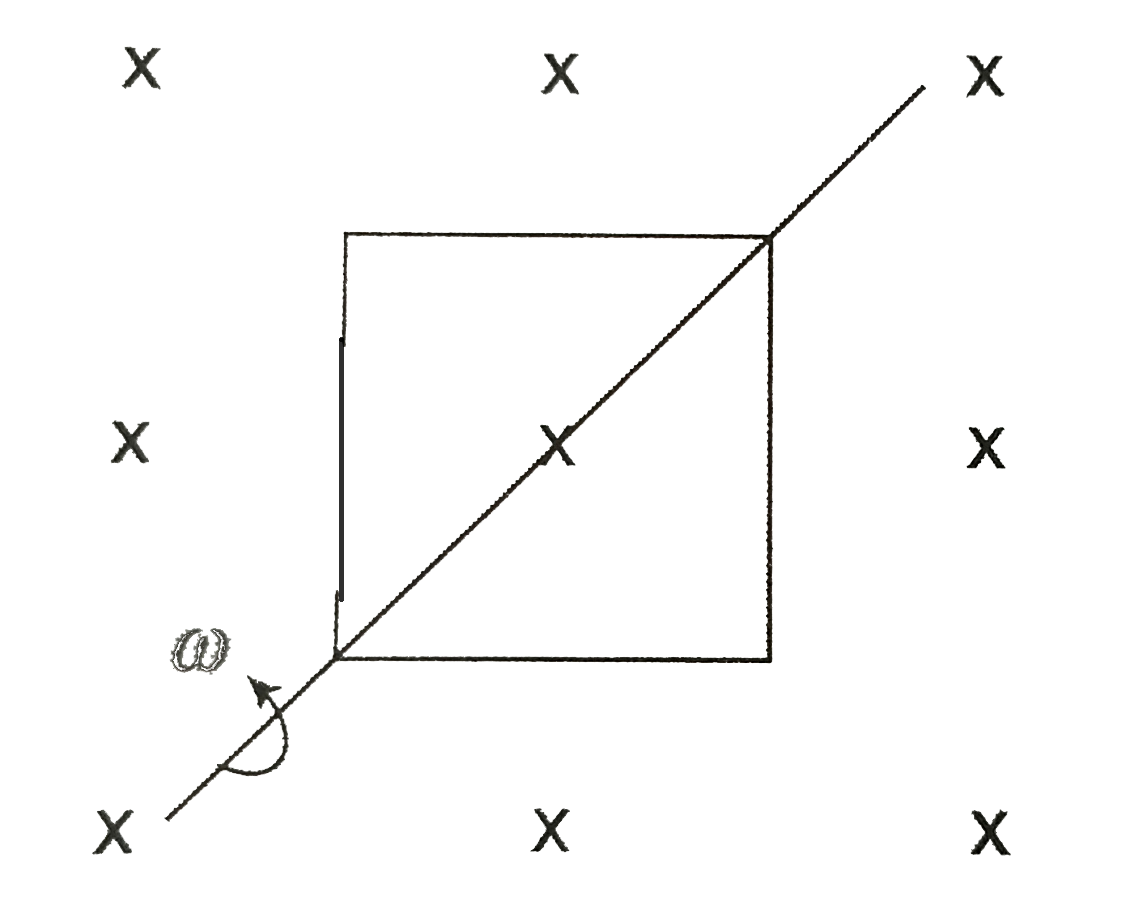
A square loop of edge a having N turns is rotated with a uniform angular velocity ω about one of its diagonals which is kept fixed in a horizontal position. A uniform magnetic field B exists in the vertical direction. Find
(a) the emf induced ion the coil as a function of time t
(b) the maximum emf induced
(c) the average emf induced in the loop over a long period (d) the average of the squares of emf induced over a long period
(e) if resistance of loop is R , amount of change flow in time t=0 to t=2T
(f) heat produced in time t=0 to =4T
 View Solution
View SolutionQuestion 12
Two straight conducting rails from a right angle where their end are joined. A conducting bar polaced over the rails starts at vertex at the time t=0 and moves with a constant velocity v to the right as shown in the figure. Calculate
(a) the flux through the triangle (isosceles) by the rails and bar at t=t0
the emf around the triangle at that time
(c) in what manner does the emf around the triangle vary with time View Solution
View SolutionQuestion 13
A current i=αt , where t is time is flowing in a long wire. A smaller circular loop of radius a has its plane parallel to the wire and is placed at distance d from the wire. If resistance per unit length of loop is λ , find the magnitude and direction of the current in the loop. View SolutionQuestion 14
A very small circular loop of area 5×I0−4m2 , resistance 2Ω and negligible inductance is initially coplanar and concentric with a much larger fixed circular loop of radius 0.Im . A constant current of IA is passed in the bigger loop and the smaller loop is rotated with angular velocity ωrad/sec about a diameter. Calculate (a) the flux limked with the smaller loop, (b) indced emf (c) induced current in the smaller loop, as a function of time.View SolutionQuestion 15
A very small circular loop of radius r is initially coplanar and concentric with a much larger circular loop of radius R(>>r) . A constant current i is passed in the larger loop which is kept fixed in space and the small loop is rotated with angular velocity ω about a diameter. The resistance of the small loop is R0 and the inductance is negligible.
(a) Find the current in the small loop as a function of time.
(b) Calculate how much troque must be exerted on the small loop to rotate it.View SolutionQuestion 16
The magnetic field in the cylindrical region shown in figure increases at a constant rate of 20.0mT/sec . Each side of the square loop abcd and defa has a length of I.00cm and a resistance of 4.00Ω . Find the cuurent (magnitude and sense) in the wire ad if:
(a) the switch SI is closed but S2 is open
(b) SI is but S2 is closed
(c) both SI and S2 are open and
(d) both SI and S2 are closed
 View Solution
View SolutionQuestion 17
A uniform magnetic field B exists in a direction perpendicular to the palne of a square frame made of copper wire. The wire has a total length of 40cm . The magnetic field changes with time at a steady rate (dB/dt)=0.02T/sec . Find the current induced in the frame. Resistance of wire =I0Ω View SolutionQuestion 18
A coil formed by wrapping 50 truns of wire in the shape of square is positioned in a magnetic field so that the normal to plane of the coil makes an angle of 60∘ , with the direction of the field. When the magnetic field is increased uniformly from 200μT to 600μT in 0.4sec , an emf of magnitude I00mV is induced in the coil. What is the total length of the wire ?View SolutionQuestion 19
A magnetic field induction is changing in magnitude at a constant rate dB/dt . A given mass m of copper is drawn into a wire into a wire of radius α and formed into a loop of radius r is placed perpendicular to the field. Show that induced current in the loop is given by im4πpδdBdt
p : resistivity, δ : density of copper. View SolutionQuestion 20
A circular coil of radius 2.00 cm has 50 turns. A uniform magnetic field B= 0.200 T exists in the space is a direction parallel to the axis of the loop. The coil is now rotated about a diameter through an angle of 60.0∘. The operation takes 0.100 s. (a) find the average emf induced in the coil. (b) if the coil is a closed one(with the two ends joined together) and has a resistance of 4.00Ω. calculate the net charge crossing a cross- section of the wire of the coil.View SolutionQuestion 21
A closed coil having 100 turns is rotated in a uniform magnetic field B=4.0×10−4 T about a diameter which is perpendicular to the field. The angular velocity of rotation is 300 revolutions per minute. The area of the coil is 25cm2 and its resistance is 4.0Ω. Find (a) the average emf developed in the half a turn form a position where the coil is perpendicular to the magnetic field, (b) the average emf in a full turn and (c) the net charge displaced in part (a).View SolutionQuestion 22
A long solenoid having 200 turns per centimeter carries a current of 1.5A. At the center of the solenoid a coil is placed of 100 turns of cross-sectional area 3.14×10−4m2 having its axis parallel to the field produced by the solenoid. When the direction of current in the solenoid is reversed within 0.05s, the induced emf in the coil is View SolutionQuestion 23
The magnetic field B shown in is directed into the plane of the paper. ACDA is a semicircular conducting loop of radius r with the centre at O. The loop is now made ot rotate clockwise with a constant angular velocity ω about on axis passing through O and perpendicular to the plane of the paper. The resistance of the loop is R. Obtain an expression for the magnitude of the induced current in the loop. Plot a graph between the induced current i and ωt, for two periods of rotation.
 View Solution
View SolutionQuestion 25
A Square frame with side a and a straigh conductor carrying a constant current I and located in the same plane. The inductance and the resistance of the frame are equal to L and R respectivaly. The frame was truned through I80∘ about the axis OO' separated from the current carrying conductor by a distance b . Find the electric charge having flown through the frame. View Solution
View SolutionQuestion 26
A square loop of edge a has N turns and a total resistance R . The loop moves with constant velocity v through a region of constant magnetic field B . The loop enters in magnetic field at t=0. Discuss the vartion of (a) Flux passing through the loop (b) the induced emf and (c) the external force acting on the loop a function of position of the loop in the field. View Solution
View SolutionQuestion 30
A plane loop is shaped ion the from as shown in the figure with radii a and b and is placed in a uniform time varying magnetic field B=B0sinωt . Find the amplitude of the current induced in the loop if its resistance per unit length is equal to λ . The inductance of the loop negligible. View Solution
View SolutionQuestion 31
A π shaped metal frame is located in a uniform magnetic field perpendicular to the plane of the conductor and varying with time at the rate (dB/dt)=0.I0T/sec . A conducting connector starts moving with an acceleration a=I0cm/sec2 along the parallel bars of the frame. The lenght o0f the connector is equal to l=20cm . Find the emf induced in the loop t=2sec after the beginnig of the motion, if at the moment t=0 the loop area and the magnetic induction are equal to zero. The inductance of the loop is to be neglected. View SolutionQuestion 33
The two rails of a railway track, insulataed form each other and from the ground, are connected to a millivoltmeter. What will be the reading of the millivoltmeter when a train travels on the track at a speed of 180kmh−1? The vertical component of earth's magnetic field is0.2×10−4 and the rails are separted by 1m.View SolutionQuestion 35
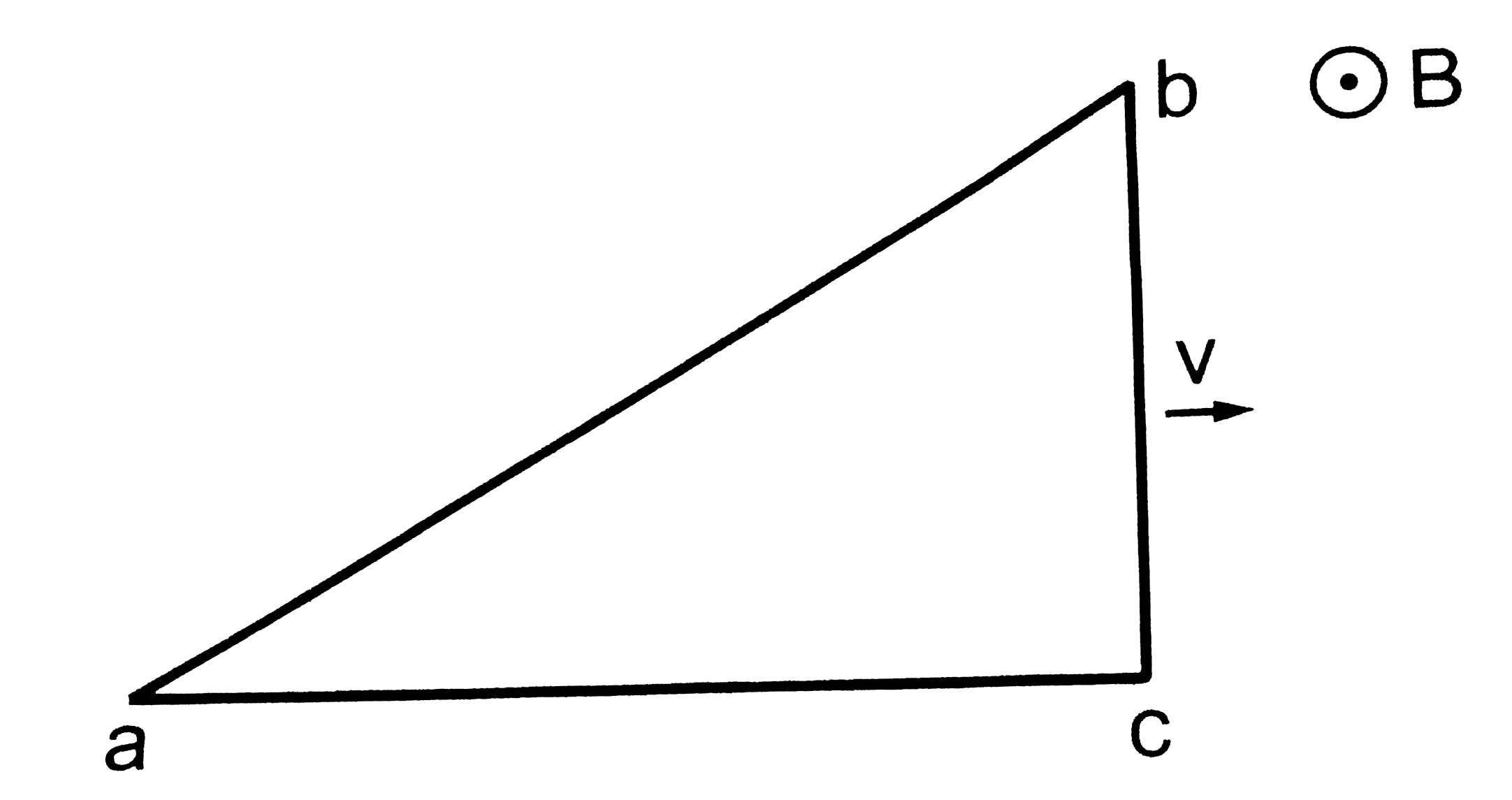
A right angled triangle abc, made from a metallic wire, moves at a uniform speed v in its plane as shown in . A uniform magnetic field B exists in the perpendicular direction. Find the emf induced (a) in the loop abc, (b) in the segment bc, (c ) in the segment ac and (d) in the segment ab.
 View Solution
View SolutionQuestion 36
A copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular ot the diameter joining free ends, (b) the velocity is parallel to this diameter.View SolutionQuestion 37
A circular copper ring of raidus r translates in its plane with a constant velocity v. A uniform magnetic field b exists in the speace in a direction perpendicular ot the plane o fhte ring. Consider different pairs of diametrically opposite points on the ring. (a) Between which pair of points is the emf? (b) Between which pair of points is the emf minimum? What is the value of this minimum emf?View SolutionQuestion 38
Two conducting rings of radii r and 2r move in apposite directions with velocities 2υ and υ respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicular to the plane of the rings. The potential difference between the highest points of the two rings is
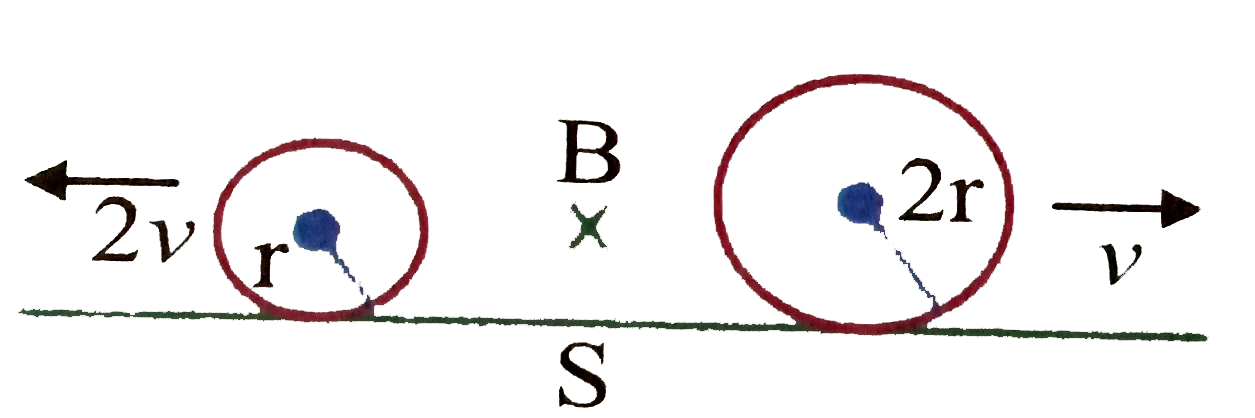 View Solution
View SolutionQuestion 39
A wire bent as a parabola y=ax2 is located in a uniformed magnetic field of induaction B , the vector B being perpendicular to the plane x−y . At moment t=0 a connector starts sliding translationwise from the parabola apex with a constant acceleration ω . Find the emf of electromagnetic induction in the loop thus formed as a function of y
 View Solution
View SolutionQuestion 41
A vertical ring of radius r and resistance on R falls vertically. It is in contact with two vertical rails which are joined at the top. The rails are without friction and resistance. There is a horizontal uniform, magnetic field of magnitude B perpendicular to the plane of the ring and the rails. When the speed of the ring is v , the current in the section PQ is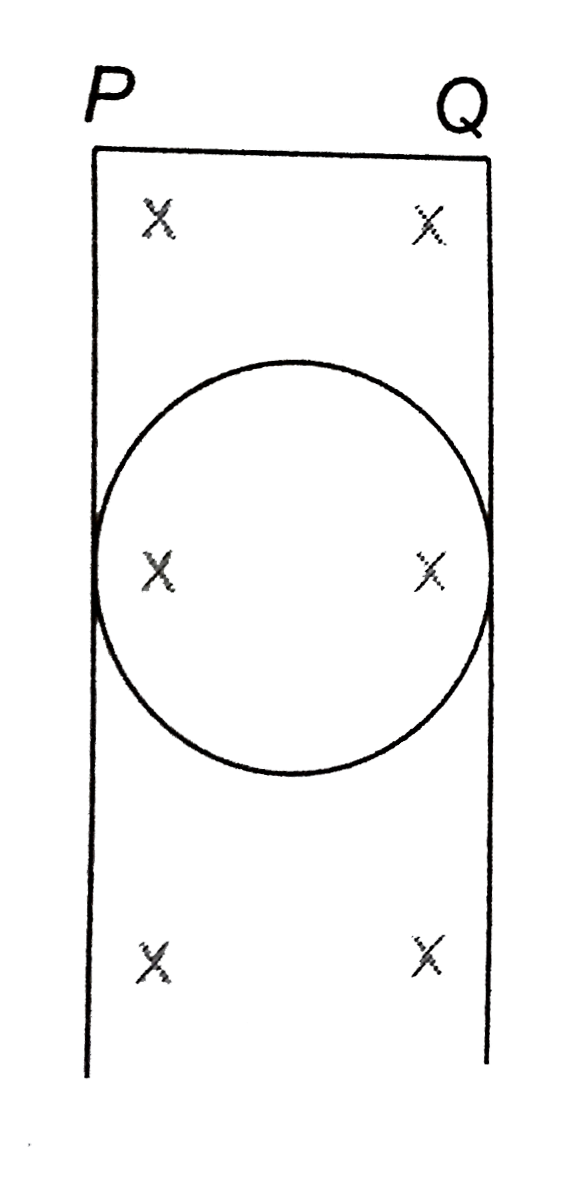 View Solution
View SolutionQuestion 42
A square metal wire loop of side 10 cm and resistance 1 ohm is moved with a constant velocity (v0) in a uniform magnetic field of induction B=2weber/m2 as shown in the figure. The magnetic field lines are perpendicular to the plane to the loop (directed into the paper). The loop is connected to a network of resistors each of value 3 ohms. The resistances of hte lead wire OS and PQ are negligible. What should be the speed of the loop so as to have a steady current of 1 milliampere in the loop? Given the direction of current in the loop.
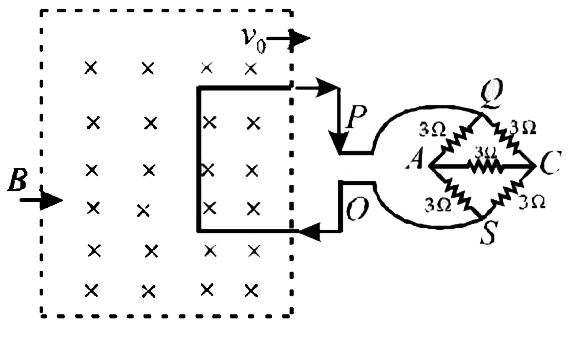 View Solution
View SolutionQuestion 43
an electric circuit is component of the three conducting rods MO , ON and PQ , as shown in the figure. The resistence of the rods per unit length is λ . The rod PQ slide, as shown in the figure, at a constant velocity v , keeping its tilt angle relative to ON and MO fixed at 45∘ . At each instance the circuit is closed. The whole system is embedded in a uniform magnetic field B , which is directe dperpendicularly into th epage. Compute the time-dependent induced electric current View Solution
View SolutionQuestion 46
Show a rectangular loop MNOP being pullled out of a magnetic field with a uniform velocity v by applying an external force F. The length MN is equal to l and the total resistance of the loop is R. Find(a) the current in the loop,(b) the magnetic force on the loop, (c) the external force F needed to magnetic the velocity, (d) the power delivered by the external force and (e) the thermal power developed in the loop.
 View Solution
View SolutionQuestion 47
A rectanguar frame of wire abcd has dimensions 32cm×8.0cm and a total resistance of 2.0Ω. It is pulled out of a magentic field B=0.020T by applying a force of 3.2×10−5 N . It is found that the frame moves with constant speed. Find (a) this constant speed, (b) the emf induced in the loop, (c) the potential difference between the points c and d.
 View Solution
View SolutionQuestion 48
In the figure shown the four rods have λ resistance per unit length. The arrangement is kept in a magnetic filed of constant magnitude B and directed perpendicular to the plane of the figure and direction inwards. Intially the sides as shown from a square. Now each wire starts moving with constant velocity v towards opposite wire. Find as a function of time:
(a) induced emf in the circuit
(b) induced current in the circuit with direction
 View Solution
View SolutionQuestion 49
Figure shows a wire ab of length L and resistance R which can slide on a smooth pair of rails. Ig is current generator which supplies a constant current i in the circuit. If the wire ab slide at a speed v towards right, find the potential difference below a and b

(b) The current generator Ig show in the figure sends a constant current i through the circiut. The wire ab has a length L and mass m and can slide on the smooth horizontal rails connect to Ig . The entire system lies in a vertical magnetic field B . Find the velocity of the wire as a function of time.

(c) The system containing the rails and the wire of the previous part is kept vertically in a uniform horizontal magnetic field B that is perpendicular to the plane of the rails (figure). If is found that the wire stays in equilibrium. If th ewire ab is replaced by another wire of double its mass, how long will lit take in falling through a distance equal to its length?
The current generator Ig shown in figure sends a constant current i through the circuit. The wire cd is fixed and wire ab is made to slide on the smooth, thick rails with a constant velocity v toward right. Each of these wires has resistance r . Find the current through the wire cd .
 View Solution
View SolutionQuestion 50
A pair of parallel horizontal conducting rails of negligible resistance shorted at one end is fixed on a table. The distance between the rails is L. A conducting massless rod of resistance R can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table, A mass m, tied to the other end of the string hanges vertically. A constant magnetic field B exists perpendicular to the table. If the system is released from rest, calculate.
(i) the terminal velocity achieved by the rod, and
the acceleration of the mass at the instant when the velocity of the rod is half the terminal velocity.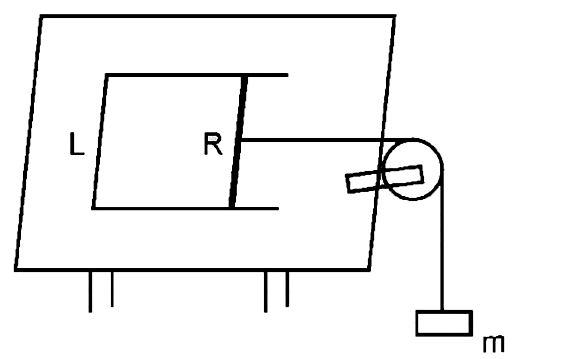 View Solution
View SolutionQuestion 51
A conducting wire ab of length l, resistance r and mass m starts sliding at t = 0 down a smooth, vertical, thick pair of connected rails as shown in . A uniform magnetic field B exists in the space in a diraction perpendicular to the plane of the rails. (a) Write the induced emf in the loop at an instant t when the speed of the wire is v. (b) what would be the magnitude and direction of the induced current in the wire? (c) Find the downward acceleration of the wire at this instant. (d) After sufficient time, the wire starts moving with a constant velocity. Find this velocity v_m. (e) Find the velocity of the wire as a function of time. (f) Find the displacement of the wire as a functong of time. (g) Show that the rate of heat developed inte wire is equal to the rate at which the gravitational potential energy is decreased after steady state is reached.
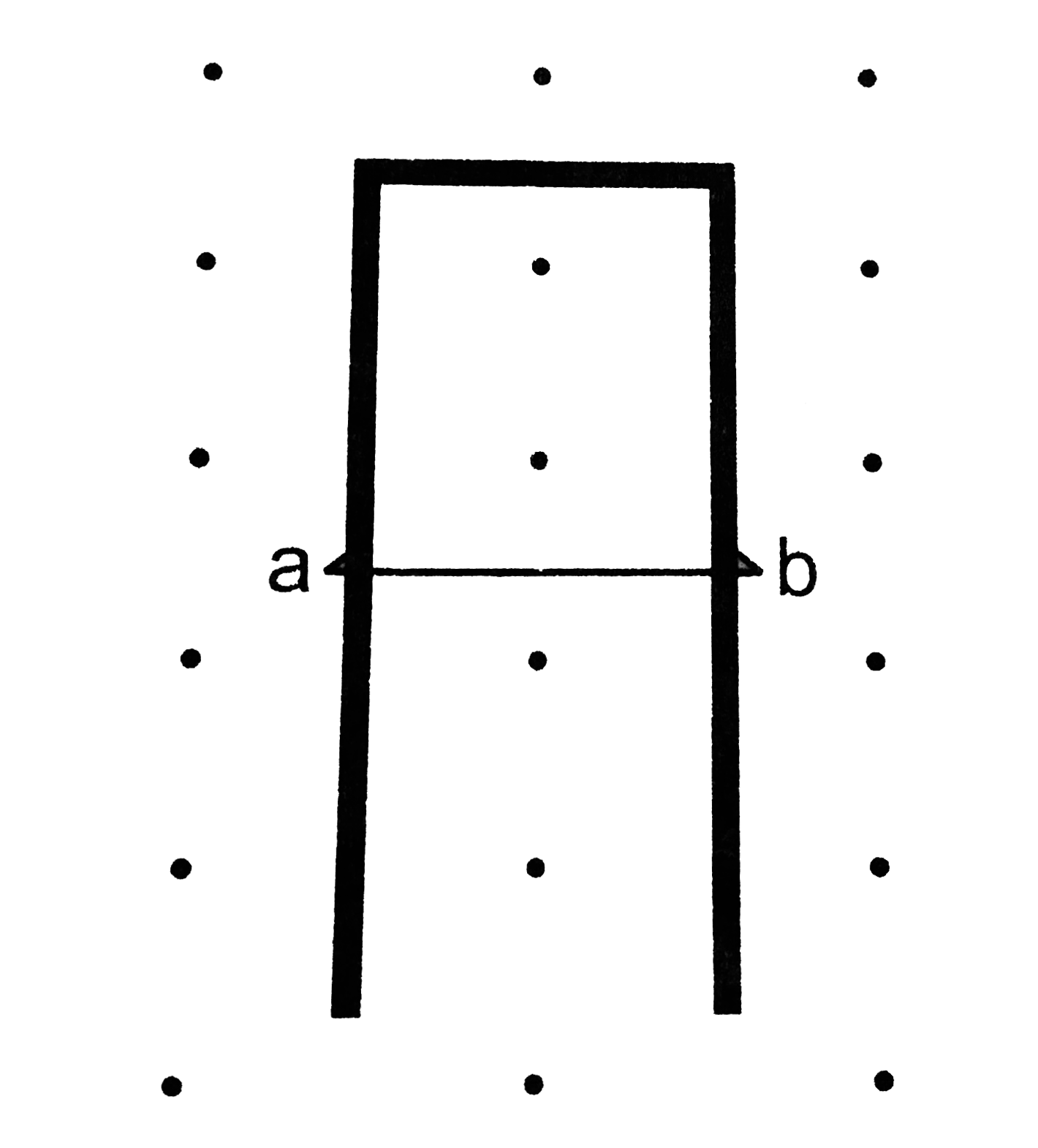 View Solution
View SolutionQuestion 52
A metal bar with length L , mass m and resistance R is polaced on frictionless metal rails that are inclined at an angle ϕ above the horizontal. The rails have negiligible resistance. There is a uniform magnetic field of nagnitude B direction download in the figure. The bar is released from rest and slide down the rails.
(a) Is the direction of the current induced in the bar from a and b or b to a ?
(b) What is the terminal speed of the bar ?
What is the induced current in the bar when the terminal speed has been reached ?
(d) After the terminal speed has been reached, at what rate is electrical energy being converted to thermal energy in the resistance of the bar ?
(e) After the terminal speed has been reached, at what rate is work being done on the bar by gravity? Compare your answer to that in part (d).
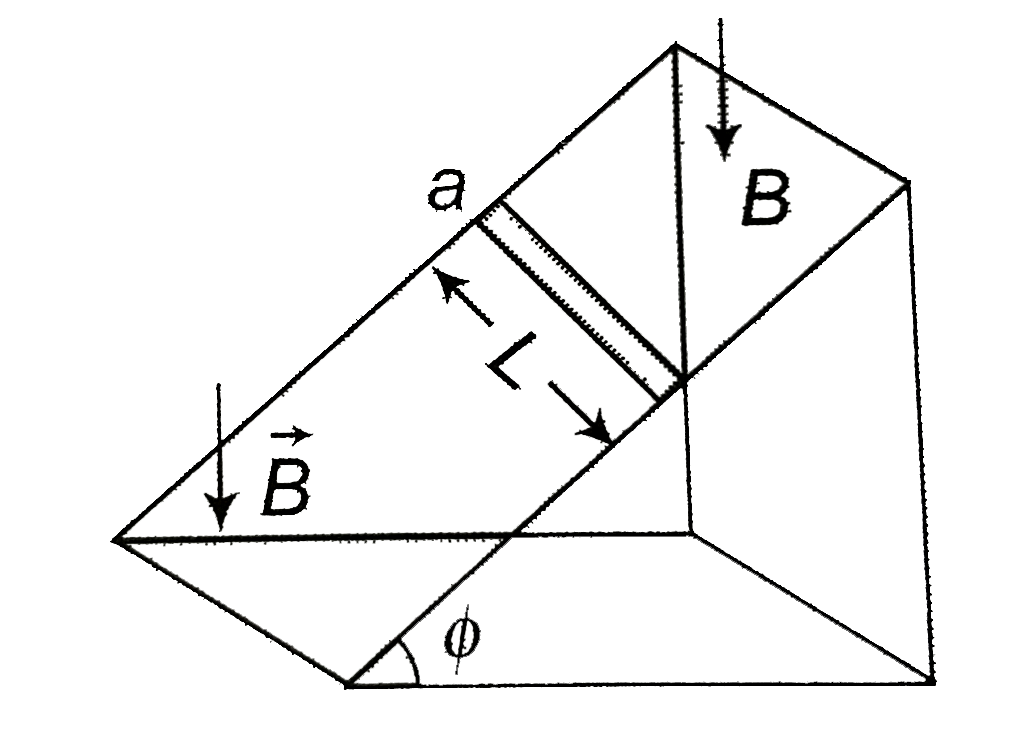 View Solution
View SolutionQuestion 53
Two metal bars are fixed vertically and are connected on the top by a capacitor C. A sliding conductor of length land mass m slides with its ends in contact with the bars. The arrangement is placed in a uniform horizontal magnetic field directed normal to the plane of the figure. The conductor is released from rest. Find the displacement x(t) of the conductor as a function of time t.
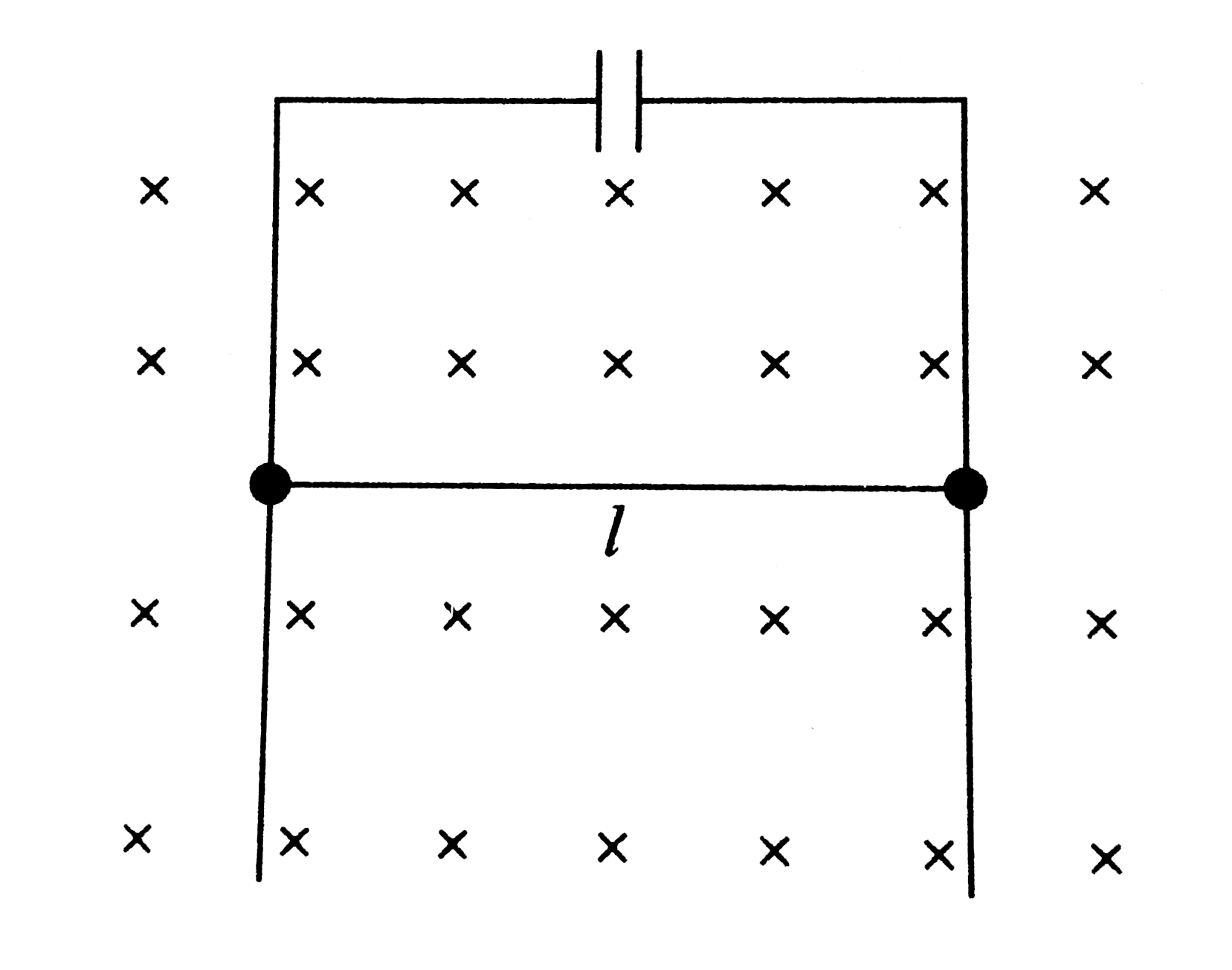 View Solution
View SolutionQuestion 54
Two parallel vertical metallic rails AB and CD are separated by 1m. They are connected at the two ends by resistances R1 and R2 as shown in the figure. A horizontal metallic bar l of mass 0.2kg slides without friction, vertically down the rails under the action of gravity. There is a uniform horizontal magnetic field of 0.6T perpendicular to the plane of the rails. It is observed that when the terminal velocity is attained, the powers dissipated in R1 and R2 are 0.76W and 1.2W respectively (g=9.8m/s2)
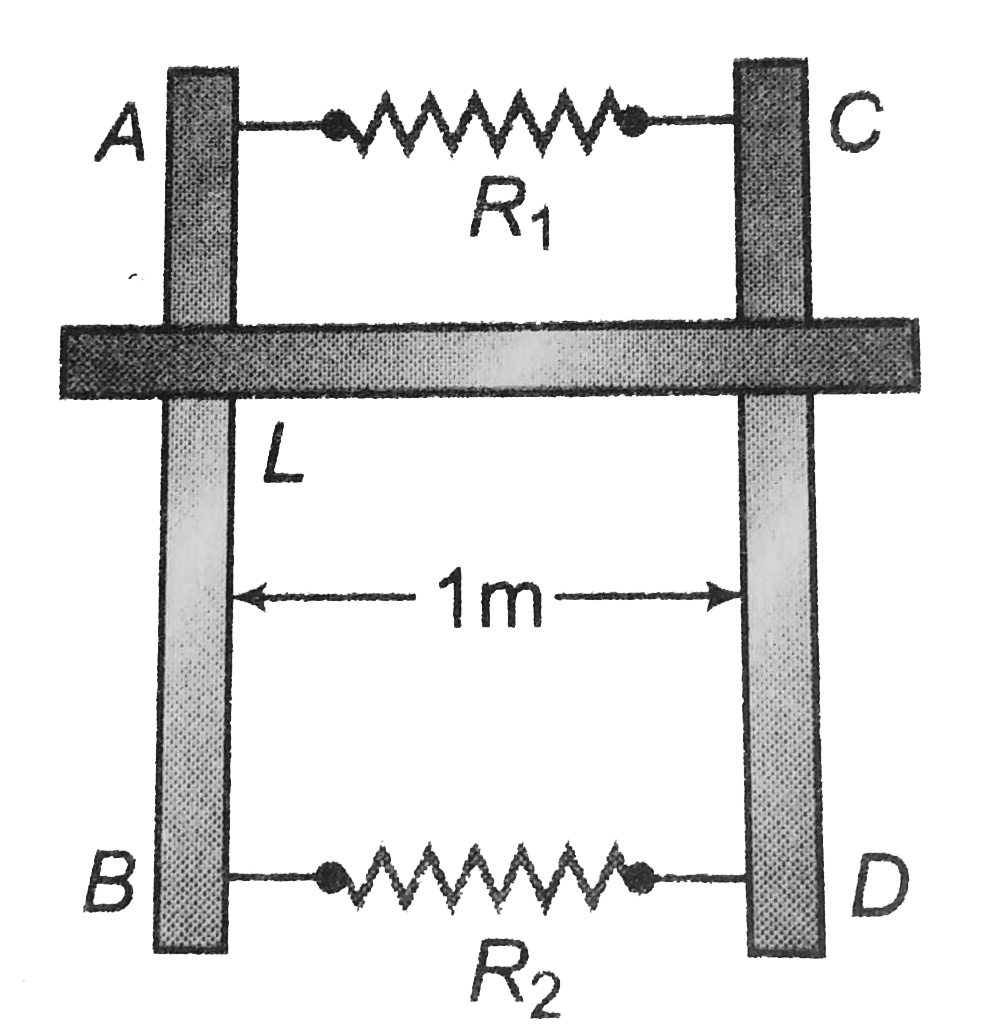
The terminal velocity fo the bar L will be View SolutionQuestion 55
shows a straight, long wire carrying a current I and a rod of length l coplanar with the wire and perpendicular to it. The rod moves with a constant velocity v in a direction parallel to the wire. The distance of the wire from the centre of the rod is x. Find the motional emf induced in the rod.
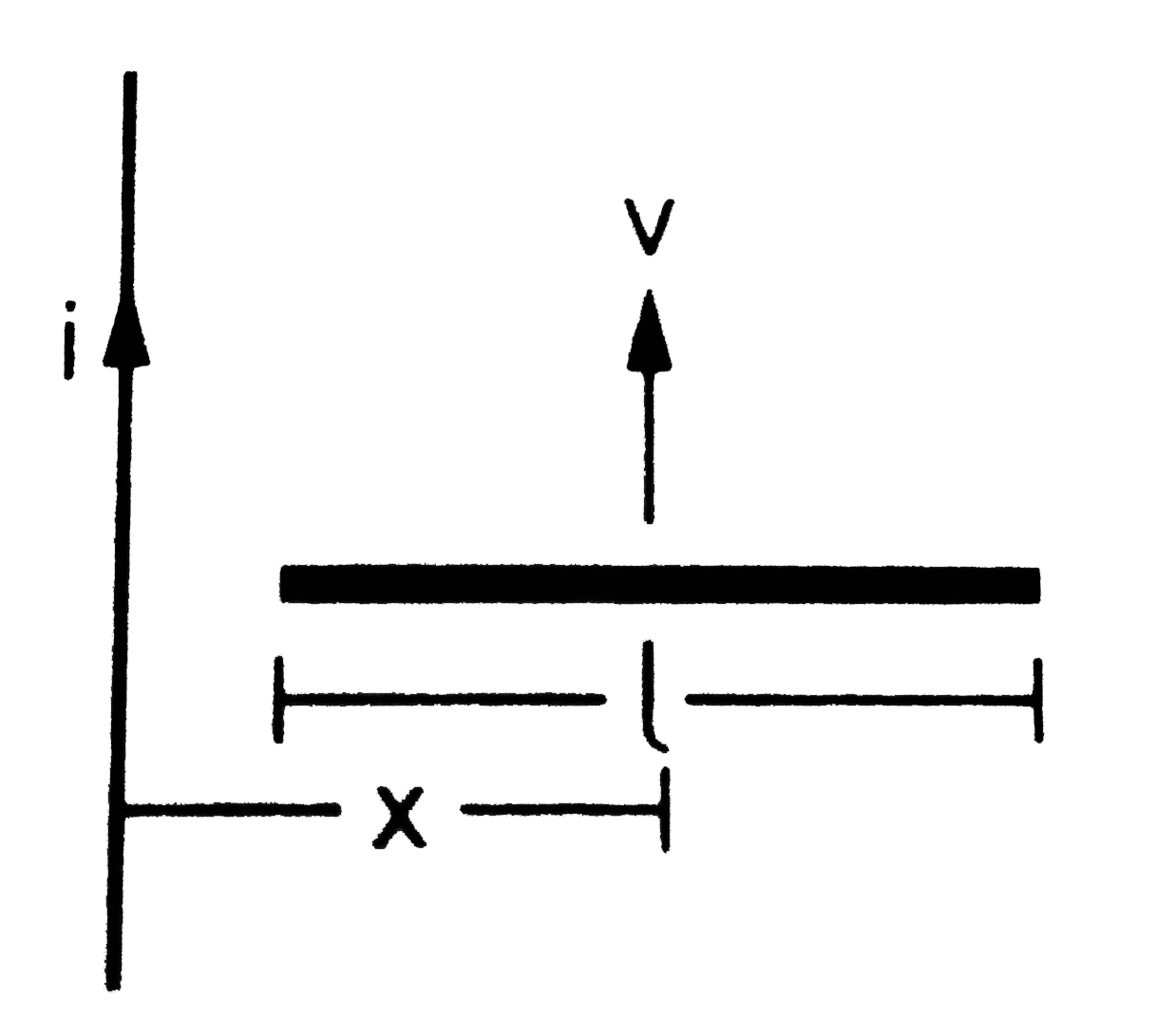 View Solution
View SolutionQuestion 57
(a) A metal rod of length L rotates about an end with a uniform angular velocity ω . A uniform magnetic field B exists in the direction of the axis of rotation. Calculate the emf induced between the ends of the rod. Neglect the centripetal force acting on the free electrons as they move in circular paths.
(b) A rod of length L rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. Find the potential difference (i) between the centre of rod and one end and (ii) between the two ends of the rod. View SolutionQuestion 58
Figure shows a conducting circular loop of radius a placed in a uniform, perpendicular magnetic field B.A thick metal rod OA is pivoted at the centre O . The other end of the rod toucher the loop are connected by a wire OC of resistance R.A force is applied at the middle point of the rod OA perpendicularly, so that the rod rotates clockwise at a uniform angular velocity ω . Find the force.
(b) Consider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance R uniformly distributed along its lenght. The rod OA is made to rotate with a uniform angular speed ω as shown in the figure. Find the current in the rod when ∠AOC=90∘ .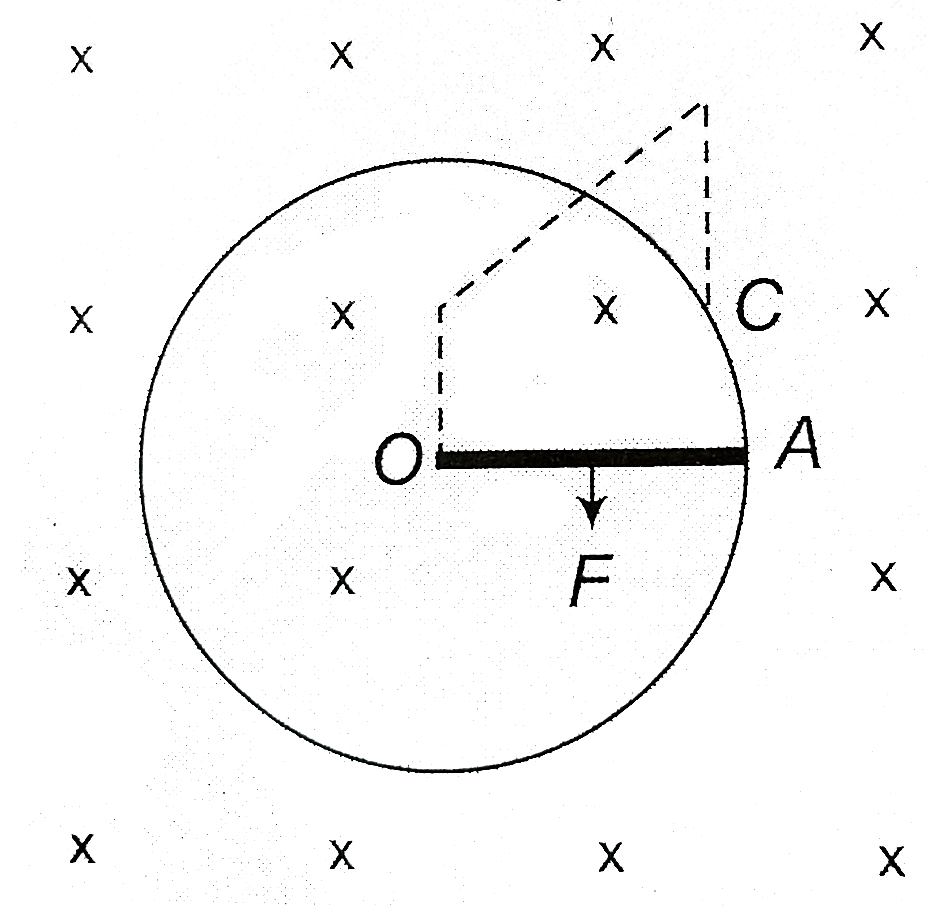 View Solution
View SolutionQuestion 60
The magnetic field at all points within the cyllindrical region whose cross section is indicated in the accompanying Figure starts increasing at a constant rate α. T/s. find the magnitud of electric field as a function of r, the distance from the geometric centre of the region. View Solution
View SolutionQuestion 61
The current in an ideal, long solenoid is varies at a uniform rate of 0.01As−1. The solenoid has 2000 turns/m and its radius 6.0 cm. (a) Consider a circle of radius 1.0 cm inside the solenoid with its axis coinciding with the axis of the solenoid. write the change in the magnetic flux through this circle in 2.0 seconds. (b) find the electric field induced at a point on the circumference of hte circle. (c) find the electric field induced at a piont outside the solenoid at a distance 8.0cm from its axis.View SolutionQuestion 62
For the situation described in figure, the magnetic field changes with time according to
B=(2.00t3−4.00t2+0.8)t and r2=2R=5.0cm

(a) Calculate the force on an electron located at P2 at t=2.00s
(b) What are the magnitude and direction of the electric field at P1 when t=3.00s and r1=0.02m. View SolutionQuestion 63
A thin non conducting ring of mass m, radius a carrying a charge q can rotate freely about its own axis which is vertical. At the initial moment, the ring was at rest in horizontal position and no magnetic field was present. At instant t=0, a uniform magnetic field is switched on which is vertically downward and increases with time according to the law B=B0t. Neglecting magnetism induced due to rotational motion of ring.
Angular acceleration of ring is View SolutionQuestion 64
(a) When the current in a coil changes from 8A to 2A in 3×10−2s , the emf induced in the coil is 2V . The self-induced of coil in mH
(b) A 12V battery conneted to a 6Ω . 10H coil through a switch drives a constant current in the circuit. The switch is suddenly opened. Assuming that it took 1msec to open the switch, calculate the average emf induced across the coil.
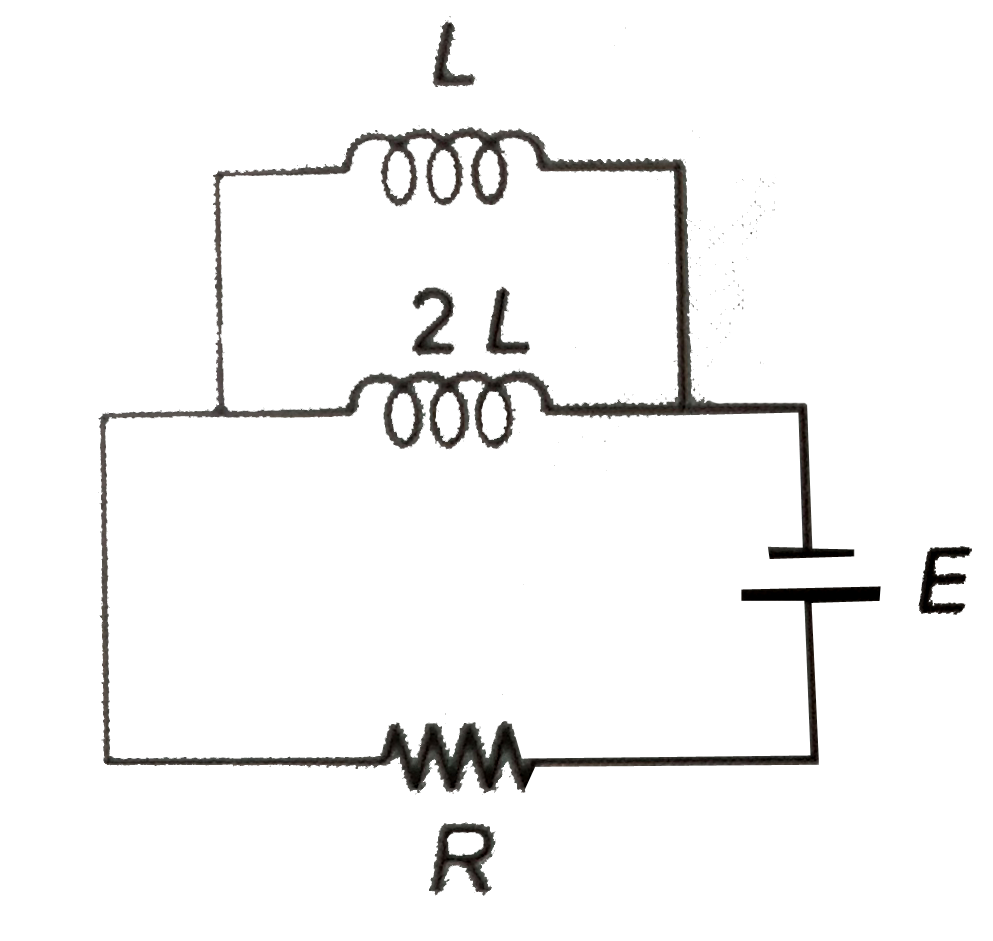
(c) The equivalent inductance of two inductored in series. What is the value of inductances of the individual inductors?
(d) If i=5A and decreasing at a rate of 103 (A/sec), find VB−BA .
 View Solution
View SolutionQuestion 67
Calculate the time constant τ of a straight solenoid of length l having a single layer winding of copper wire whose total mass is equal to m . The cross-sectional dimater of the solenoid is assumed to be considerably less than its length. Given desity of copper p0 and resistivility p .View SolutionQuestion 68
A supereconducting round ring of radius a and inductance L was located in a uniform in a uniform magnetic field of induction B . The ring plane was parallel to the vector B and the current in the ring was equal to zero, then the ring was turned through 90∘ so that its plane became perpendicular to the field. Find
(a) the current induced in the ring after the turn
(b) the work performed during the turn. View SolutionQuestion 70
Two different coils have self-inductances L1=8mH and L2=2mH At a certain instance the current in thw two coils is increasing at the same constant rate and the power supplied to the coils is the same. Find the ratio of (a) induced voltage (b) current (c) energy stored i the two coils at that instant. View SolutionQuestion 81
A coil has 600 turns which produces 5×10−3Wb/turn of flux when 3A current flows in the wire. This produced 6×10−3 Wb/turn in 1000 turns secondary coil. When the opened, the current drops to zero in 0.2s in primary. Find
(a) mutual inductance,
(b) the induced emf in the secondary,
(c) the self-inductance of the primary coil. View SolutionQuestion 82
A circular coil P of 100 turns and radius 2cm is placed coaxially at the centre of another circular coil Q of 100 turns and radius 20cm . Calculate (a) the mutual inductance of the coils
(b) the induced emf in coil P when the current in the coil Q decreases from 5A to 3A in 0.04 sec (Take π2=10)View SolutionQuestion 89
A solenoid having inductance 4.0 H and resistance 10Ω is connected to a 4.0 V battery at t = 0. Find (a) the time constant, (b) the time elapsed before the current reached 0.63 of its steady state value, (c ) the power delivered by the battery at this instant and (d) the power dissipated in Joule heating at this instant. View SolutionQuestion 90
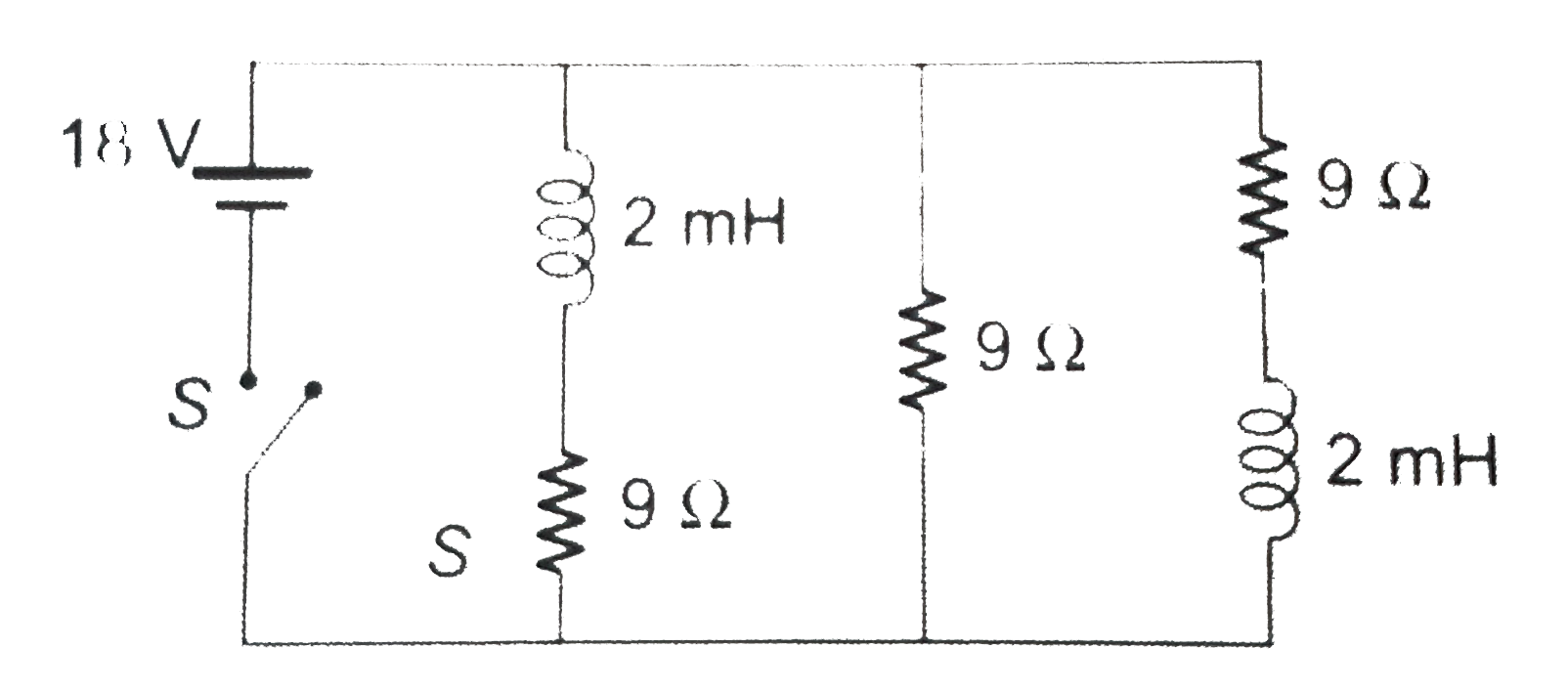
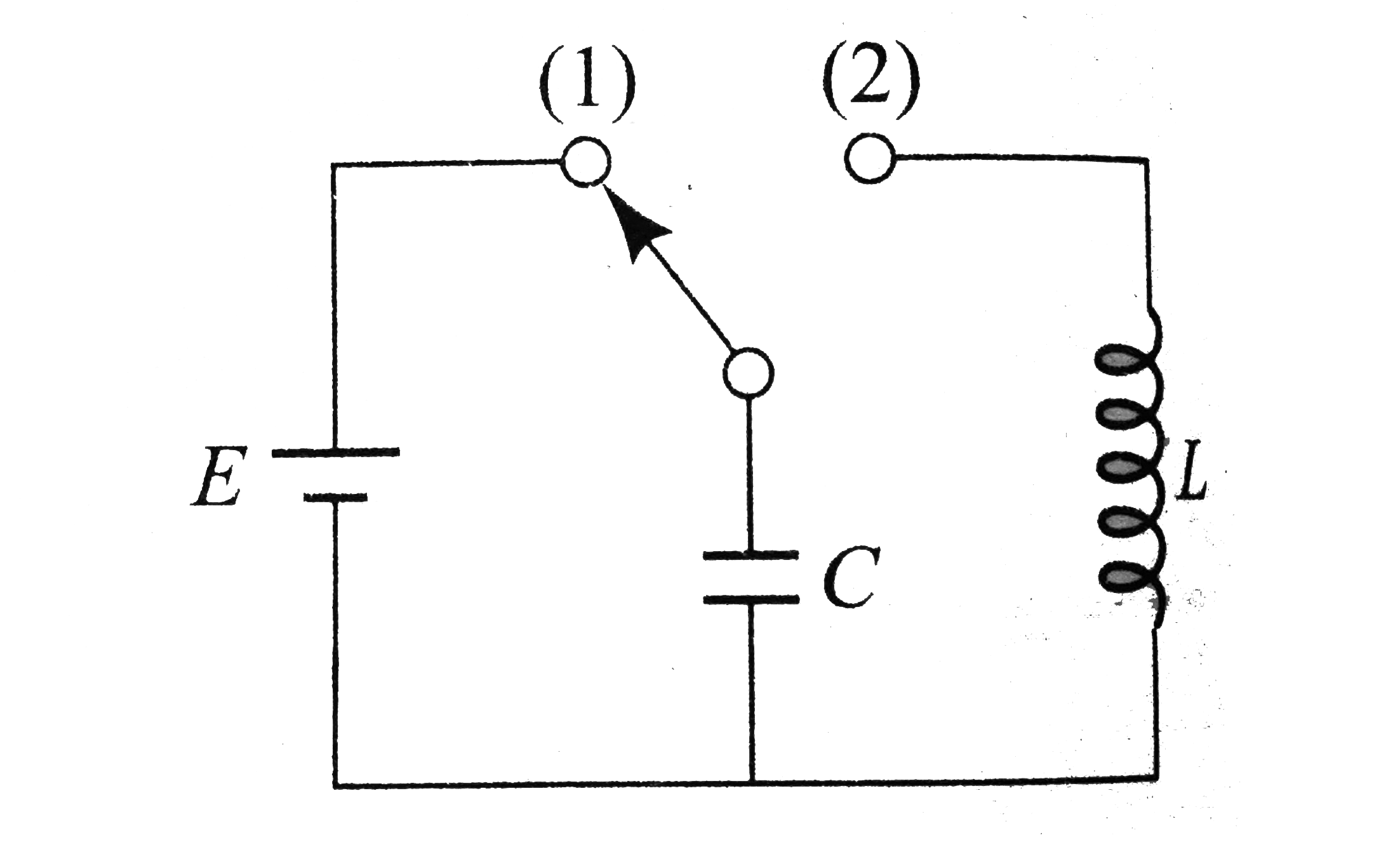
At t=0 , switch S is closed, calculate
(a) initial rate of increase of current i.e. didt at t=0
(b) didt at time when current in the circiut is 1A
(c) current at t=0.5sec
(d) rate at which energy of magnetic field is incresing, rate of heat produced in resistance and rate at which energy is supplied by battery when i=1A
(e) energy stored in inductor in steady state
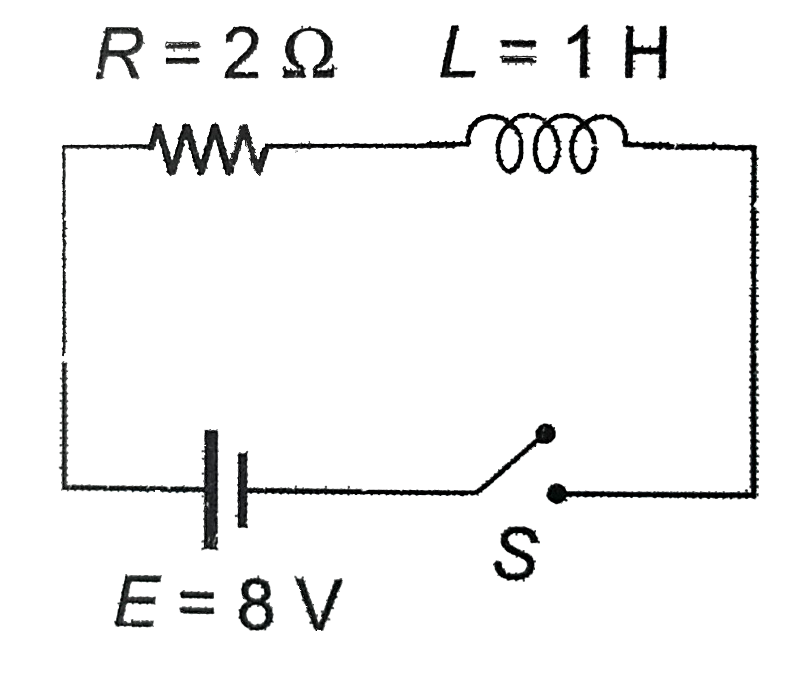 View Solution
View SolutionQuestion 95
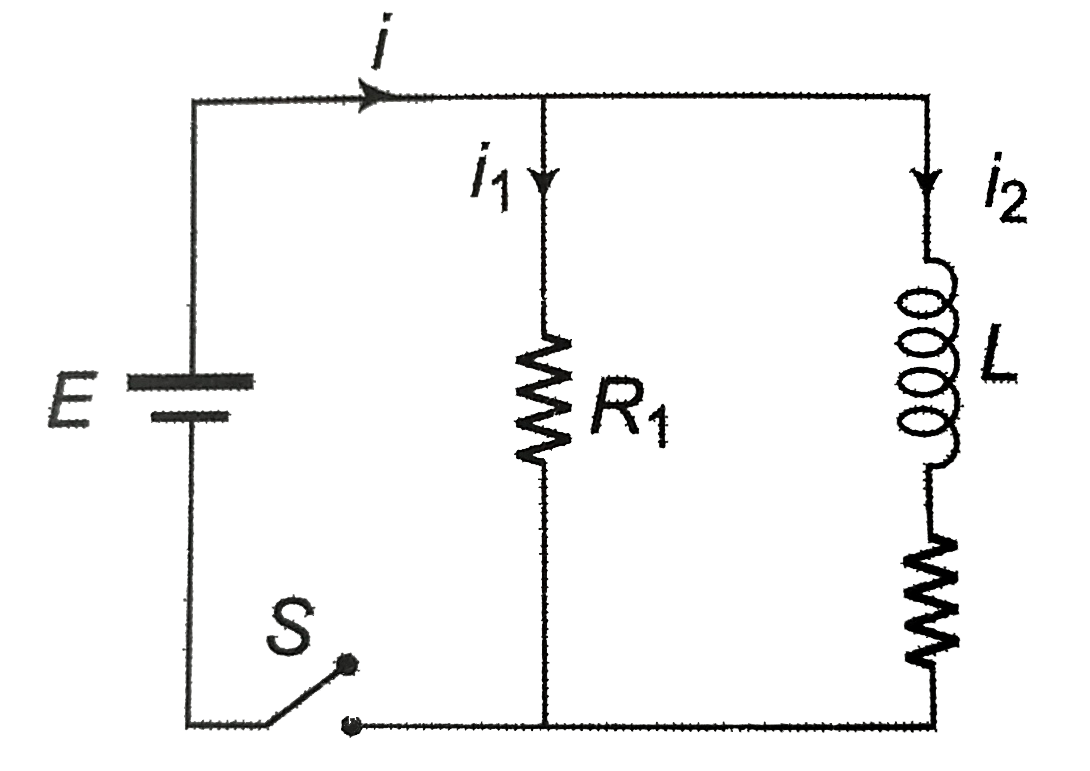
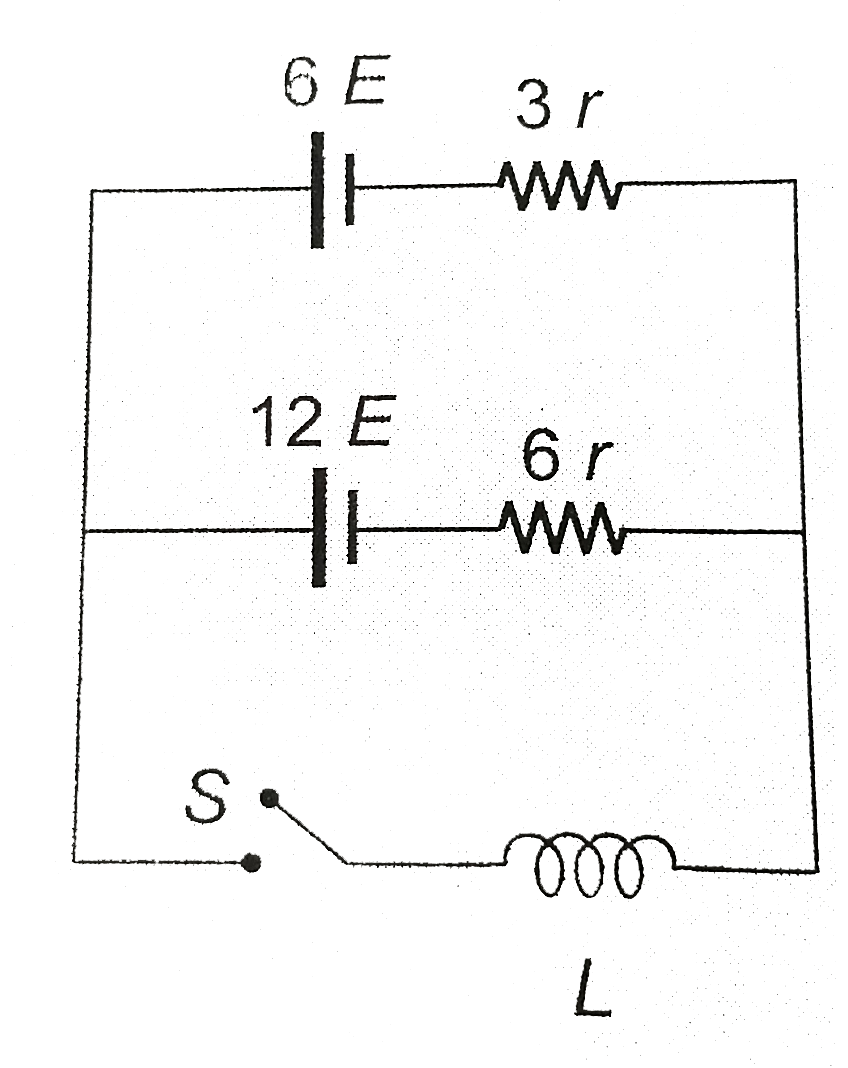
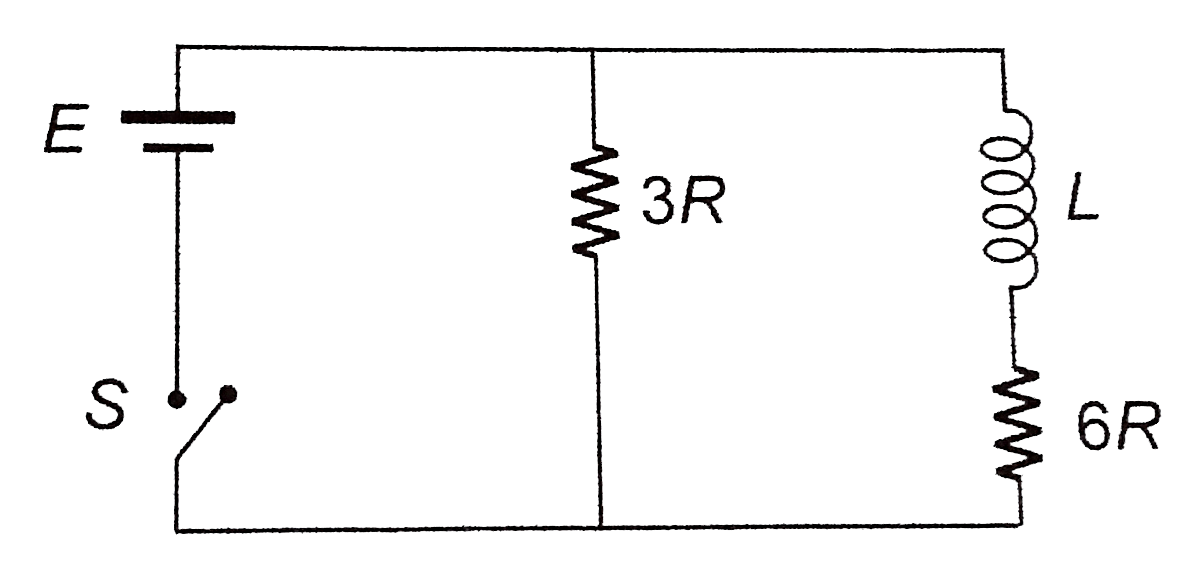
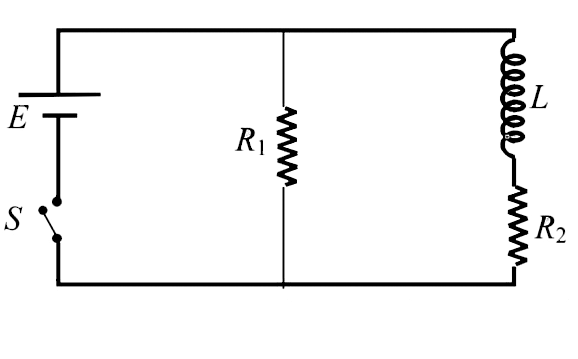
An inductor of inductance L=400 mH and resistor of resistance R1=2(Ω)andR2=2(Ω) are connected to a battery of emf E = 12 Vas shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at time t =0. What is the potential drop across L as a function of time? After the steady state is reached, the switch is opened. What is the direction and the magnitude of current through R1 as a function of time?
 View Solution
View SolutionQuestion 97
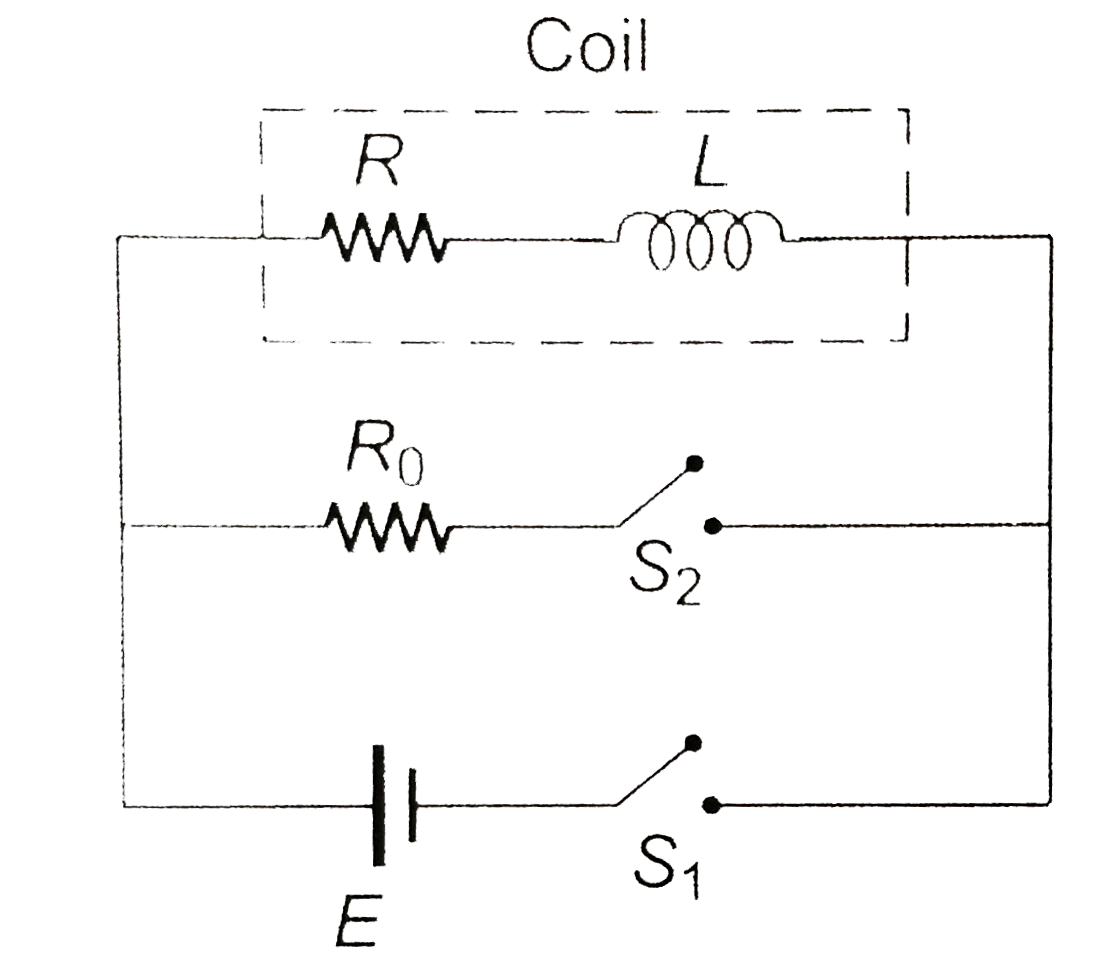
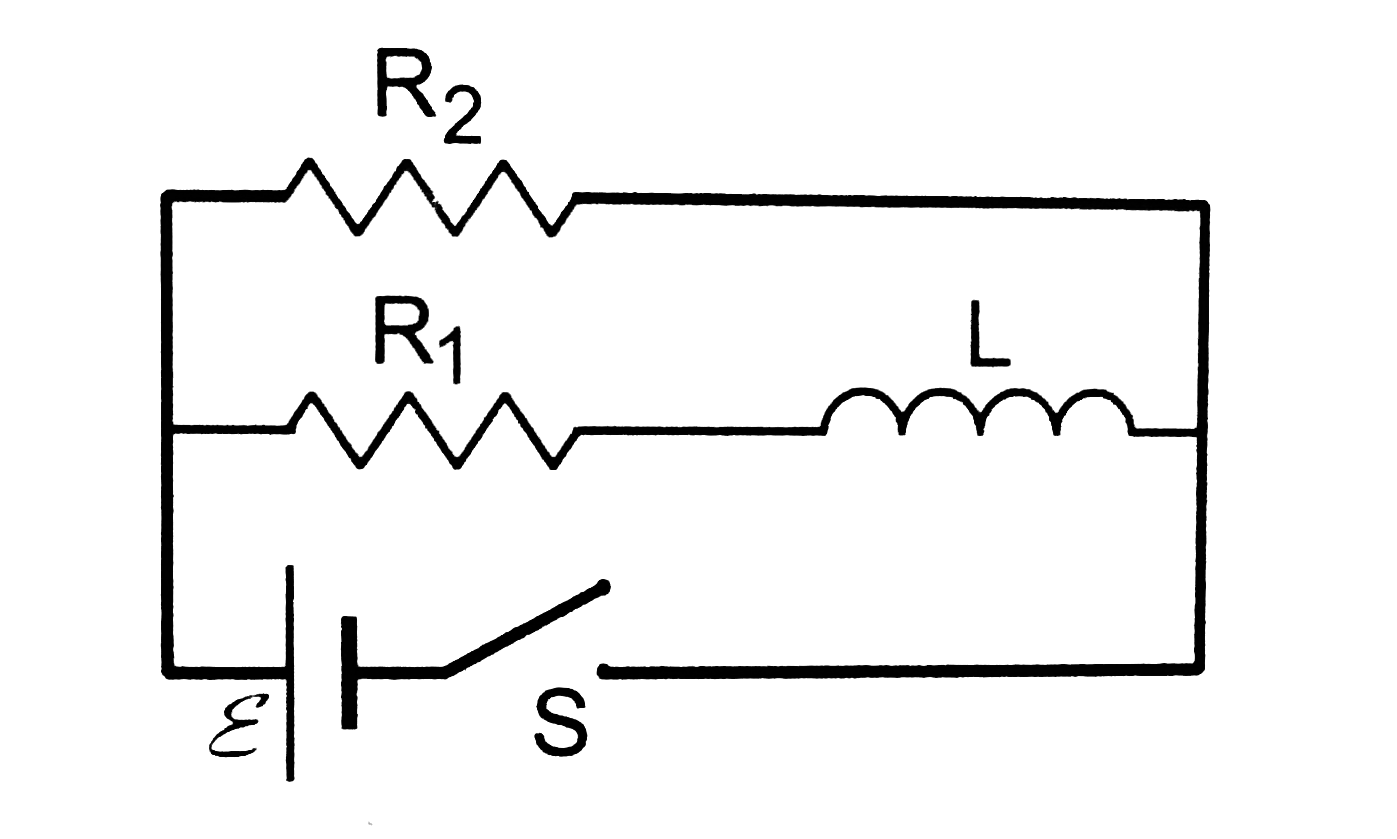
Consider the circuit shown in .(a) find the current through the battery a long time after the switch S is closed. (b) Suppose the switc is again opened at t = 0. What is the time cosstant of the discharging circuit? (c ) Find t current through the inductor after one time constant.
 View Solution
View SolutionQuestion 101
An inductor of inductance 2.0mH is connected across a charged capacitor of capacitance 5.0μF and the resulting L−C circuit is set oscillating at its natural frequency. Let Q denote the instantaneous change on the capacitor and i the current in the circuit. It is found that the maximum value of Q is 200μC .
(a) When Q=100μC , what is the value of |di/dt| ?
(b) When Q=200μC , what is the value of i ?
(c)Find the maximum value of i
(d) When i is equal to one-half its maximum value, what is the value of |Q| ? View SolutionQuestion 103
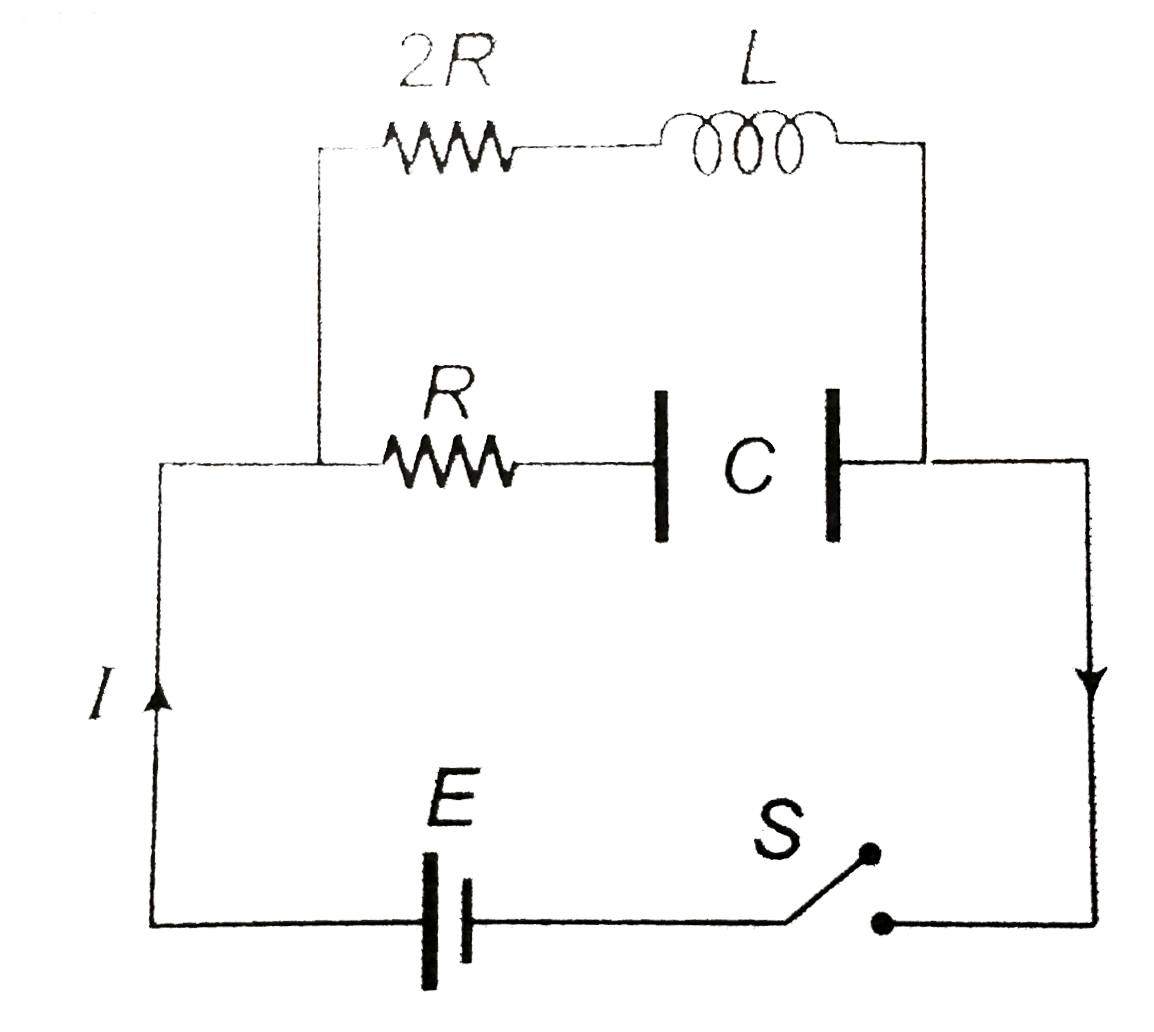
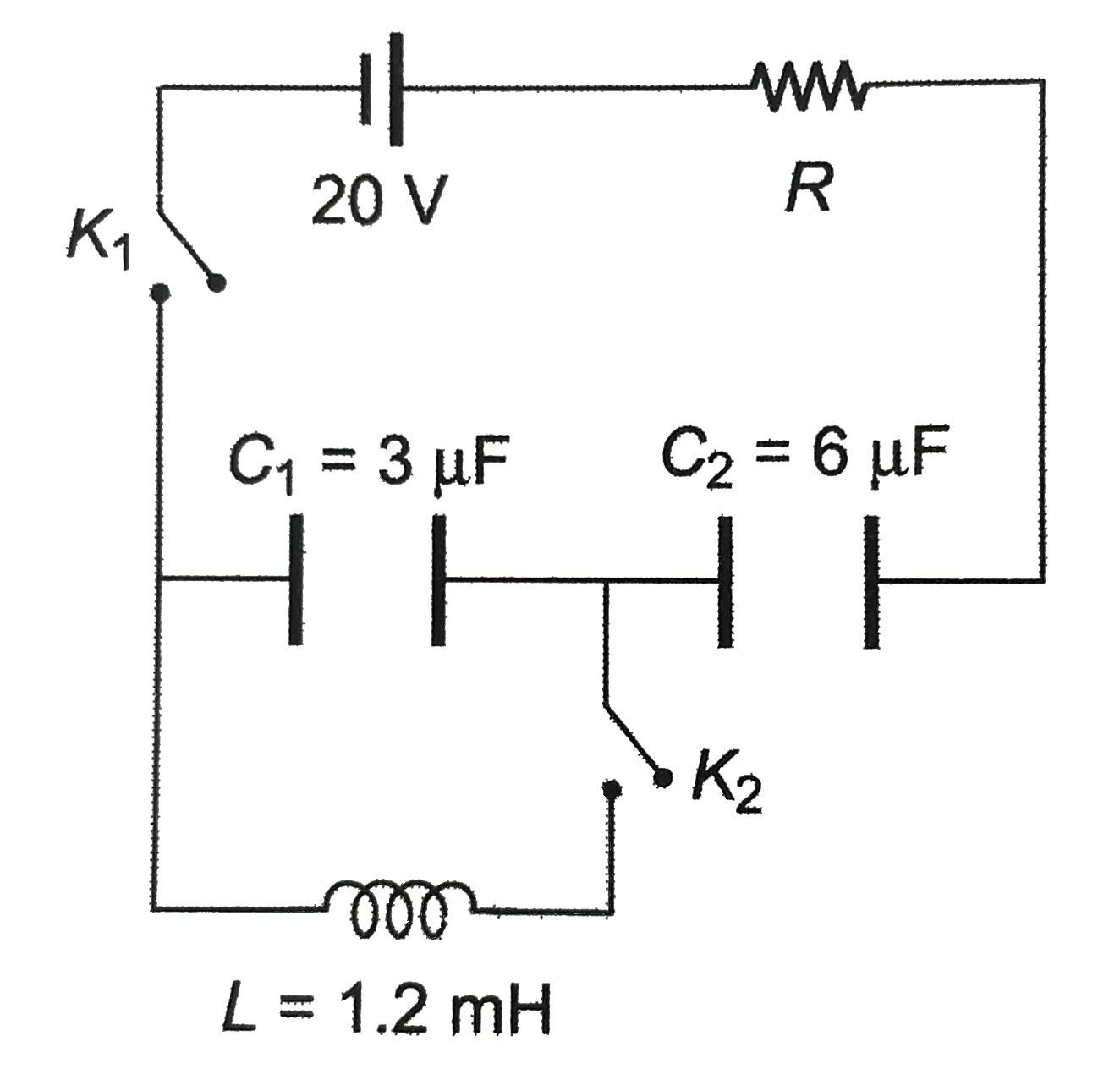
A circuit containing capacitors C1 and C2 shown in the figure is in the steady state with key K1 cloesed. At the instant t=0 , K1 is opened and K2 is closed.
(a) Find the angular frequency of oscillation of the LC circuit.
(b) Determine the first instant t , when enregy in the indctor becomes one third of that in the capacitor.
(c) Calculate the change on the plates of the capacitor at that instant.
 View Solution
View SolutionQuestion 104
Shows a square frame of wire having a total resistance r placed coplanarly with a long, straight wire. The wire carries a current I given by i=i0sinωt. Find(a) the flux of the magnetic field through the square frame, (b) the emf induced in the frame and (c) the heat developd in the frame in the time interval 0 to 20πω.
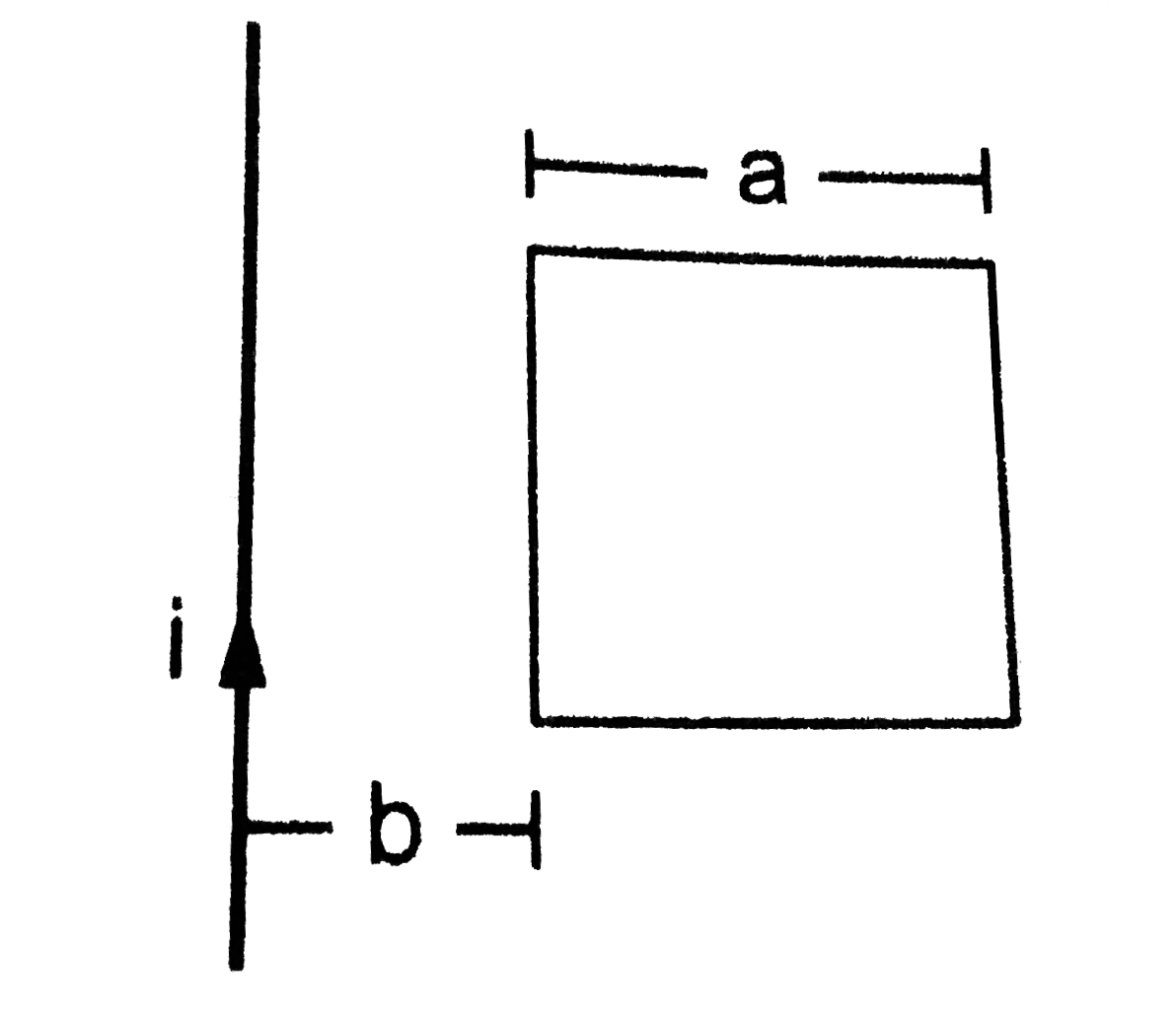 View Solution
View SolutionQuestion 106
An infinitesimal bar magnet of dipole moment M is pointing and moving with speed v in the x-direction. A closed circular conducting loop of radius a ans negligible self-inductance lies in the y−z plane with its centre at x=0 and its axis coinciding with x-axis. find the force opposing the motion of the magnet, if the resistance of the loop is R . Assume that the distance x of the magnet from the centre of the loop is much greater than a . View SolutionQuestion 107
Consider the situation shown in the figure. The wire PQ has mass m , resistance r and can slide 0n the smooth, horizontal parallel rails separated by a distance l . The resistance of the rais is negiligible. A uniform magnetic field B exists in the reactangular region and a resistance R connects the rail outside the field region. At t=0 , the wire PQ is pushed toward right with a speed v0 . Find
(a) the current in the loop at an instant when the speed of the wire PQ is v
(b) the acceleration of the wire as this instant
(c) the velocity v as a function of x
(d) the maximum distance the wire will move
(e) the velocity as a function of time
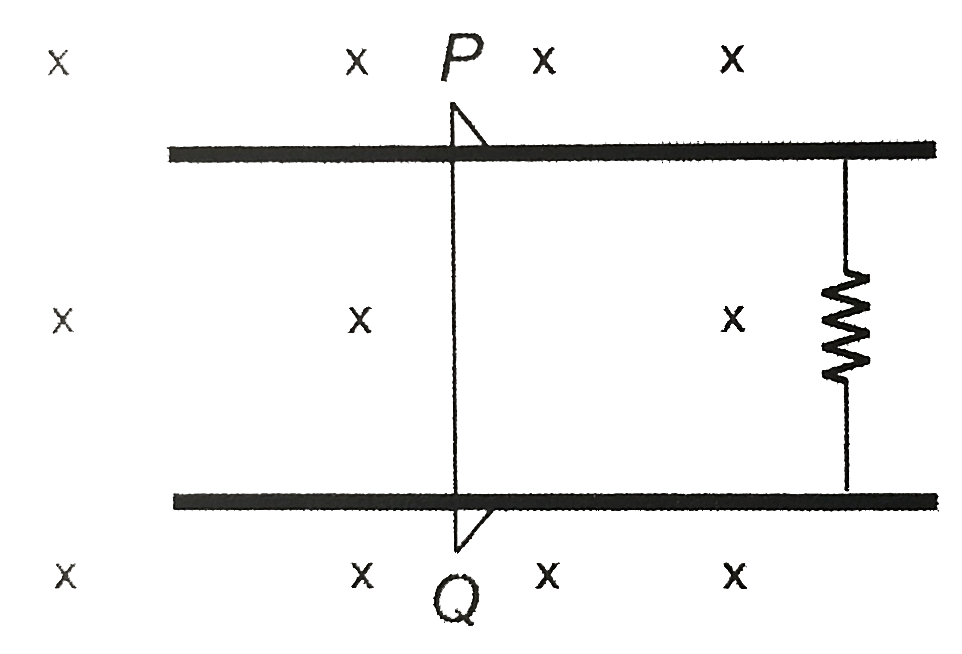 View Solution
View SolutionQuestion 108
Two long parallel wires of zero resistance are connected to each other by a battery of 1.0V . The separation between the wires is 0.5m . A metallic bar, which is perpendicular toi the wire and of resistance 10Ω moves on these wire when a magnetic field of 0.02 tesla is acting p endicular to the plane containing the wire and the wires. Find the velocity of the bar as a function of time if the mass of the bar is 0.002kg . Find also the steady-state velocity of the bar. View SolutionQuestion 111
A loop is formed by two parallel conductors connected by a solenoid with inductance L and a conducting rod of mass m which can freely (without friction) slide over the conductors. The conductors are located in a horizontal plane in a uniform vertical magnet field B . the distance between the conductors is l . At the moment t=0 , the rod is imparted an initial velocity v0 directed to the right. Find the law of its motion x(t) if the electric resistance of the loop is negligible.
 View Solution
View SolutionQuestion 112
A coil of inductance L connects the upper ends of two vertical copper bars separated by a distance l . A horizontal conducting connector of mass m starts falling with zero initial velocity along the bars without losing contact with them. The whole system is located in a uniform magnetic field B perpendicular to the plane of the bars. Find the law of motion x(t) of the connector.
 View Solution
View Solution