exercise from HC VERMA PHYSICS (ENGLISH) Chapter 14 MAGNETIC FIELD DUE TO CURRENT for Class 12

Question 1

Question 2

Question 3

Question 4

Question 5

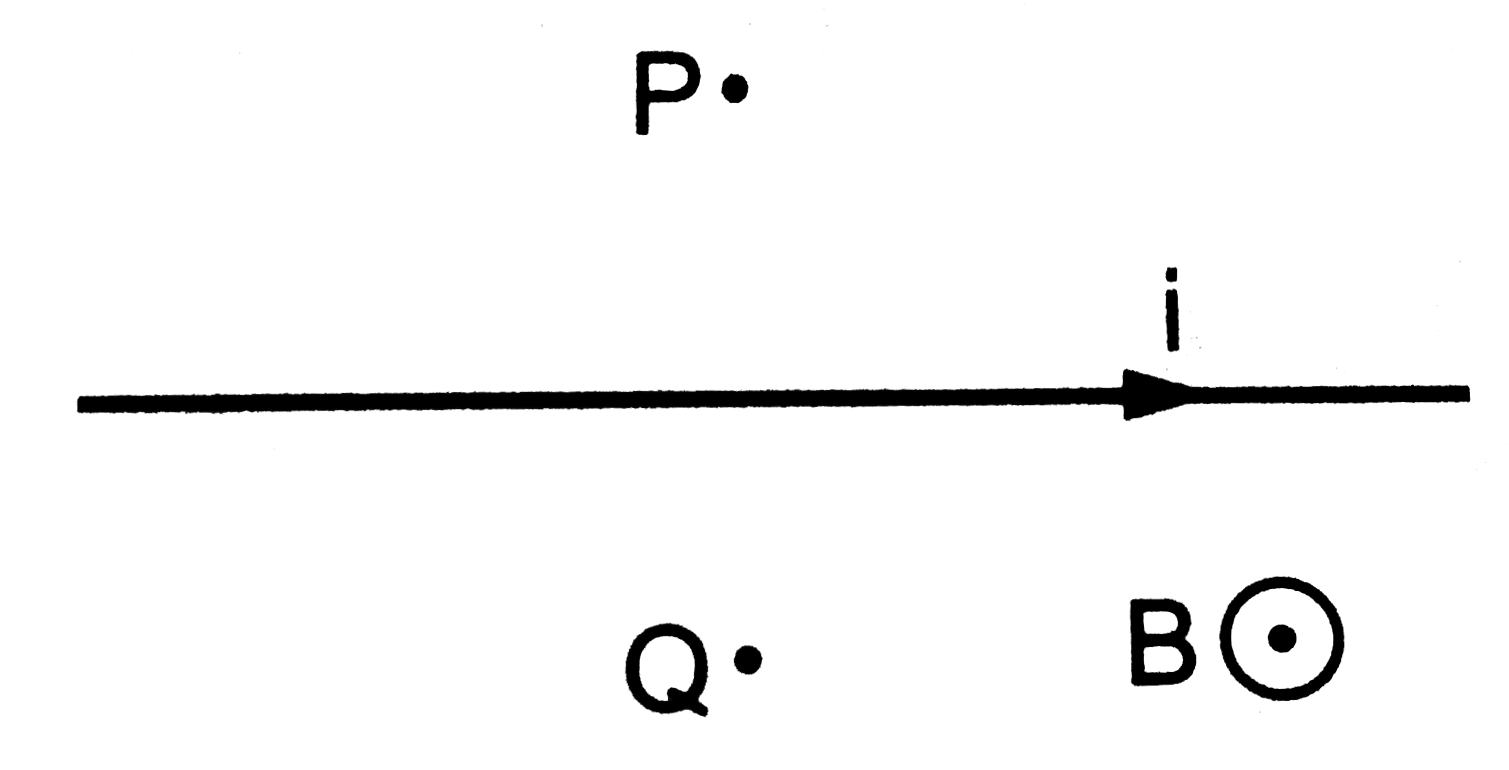
A long, straight wire carrying a current of 1.0 A is placed horizontally in a uniform magnetic field B= ($1.0\times {10}^{-5})$ T pointing vertically upward. Find the magnitude of the resultant magnetic field at the points P and Q, both situated at a distance of 2.0 cm from the wire in the same horizontal plane.

Question 6

Question 7

Question 8

Question 9

Figure shows two parallel wires separated by a distance of 4.0 cm and carrying equal currents of 10A along opposite directions. Find the magnitude of the magnetic field B at the points $A_1,A_2,A_3\text{and}{A}_4.$

Question 10

Question 11

Question 12

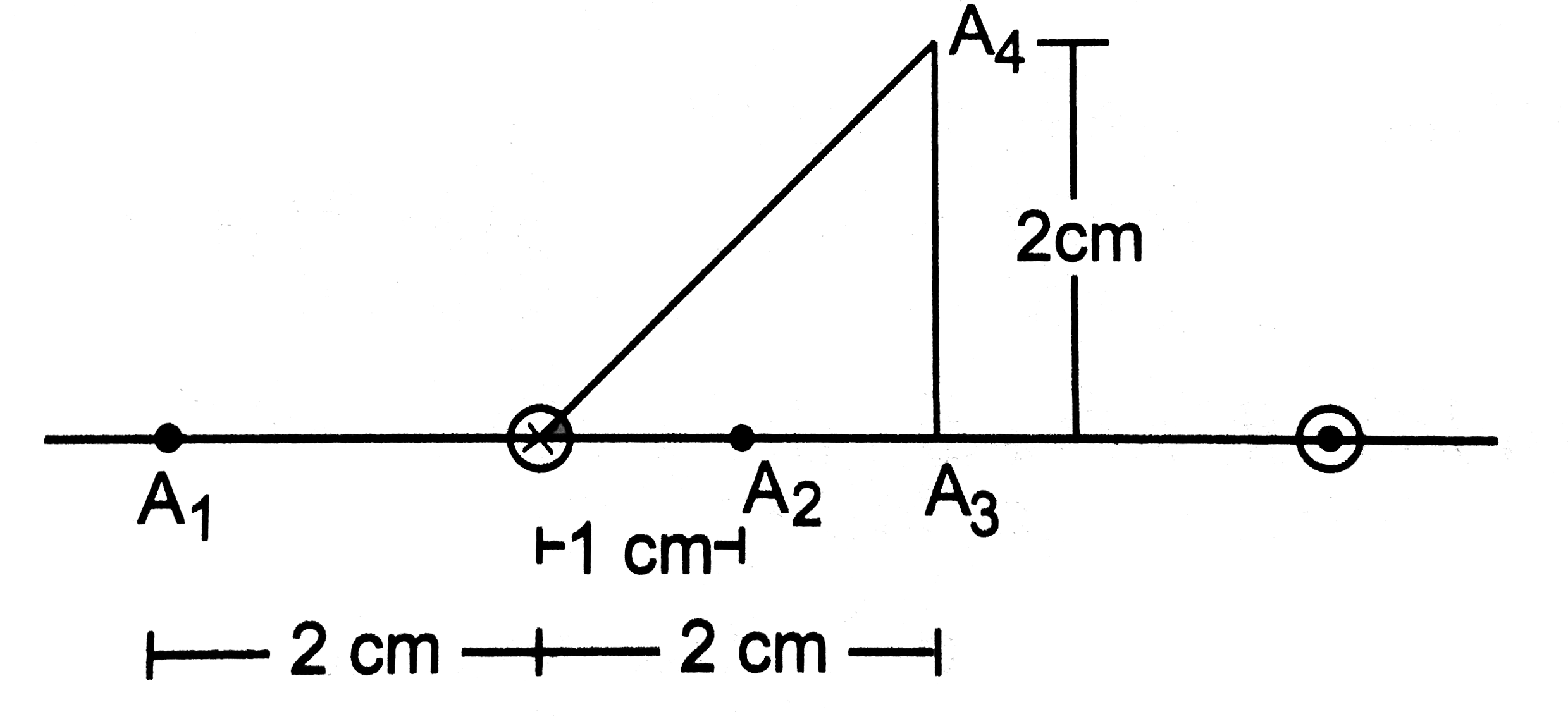
Four long, straight wires, each carrying a current of 5.0 A, are placed in a plane as shown in figure . The points of intersection form a square of side 5.0 cm. (a) Find the magnetic field at the centre P of the square. (b) $Q_1,Q_2,Q_3\text{and}{Q}_4$ are points situated on the diagonals of the square and at a distance from P that is equal to the length of the diagonal of the square. Find the magnetic fields at these points.

Question 13

Figure shows a long wire bent at the middle to form a right angle. Show that the magnitudes of the magnetic fields at the points P,Q, R and S are equal and find this magnitude.

Question 14

Question 15

Question 16

Question 17

Figure shows a square loop ABCD with edge length a. The resistance of the wire ABC is r and that of ADC is 2r. Find the magnetic field B at the centre of the loop assuming uniform wires.

Question 18

The wire ABC shown in figure forms an equilateral triangle. Find the magnetic field B at the centre O of the triangle assuming the wire to be uniform.

Question 19

Question 20

Question 21

Question 22

Question 23

Each of the batteries shown in figure has an emf equal to 5 V. Show that the magnetic field B at the point P is zero for any set of values of the resistances .

Question 24

Question 25

Question 26

Question 27

Figure shows a part of an electric circuit. The wires AB, CD, and EF are long and have identical resistances. The separation between the neighbouring wires is 1.0 cm. The wires AE and BF have negligible resistances and the ammeter reads 30 A . Calculate the magnetic force per unit length of AB and CD.

Question 28

Question 29

A square loop PQRS carrying a current of 6.0 A is placed near a long wire carrying 10 A as shown in figure . (a) Show that the magnetic force acting on the part PQ is equal and opposite to that on the part RS. (b) Find the magnetic force on the square loop.

Question 30

Question 31

Question 32

Question 33

A conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.

Question 34

Question 35

Question 36

Question 37

Question 38

Question 39

Question 40

Question 41

Question 42

Question 43

Question 44

Question 45

Question 46

Question 47

Question 48

Question 49

Sometimes we show an idealised magnetic field which is uniform in a given region and falls to zero abruptly. One such field is represented in figure . Using Ampere's law over the path PQRS, show that such a field is not possible.

Question 50

Two large metal sheets carry surface currents as shown in figure . The current through a strip of width dl is Kdl where K is a constant . Find the magnetic field at the points P,Q and R.

Question 51

Question 52

Question 53

Question 54

Question 55

Question 56

Question 57

Question 58

Question 59