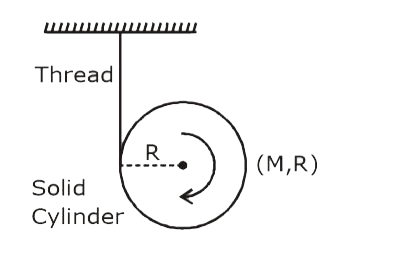
A light thread with a body of mass $m$ tied to its end is wound on a uniform solid cylinder of mass $M$ and radius $R$ . At a moment $t = 0$ the system is set in motion. Assuming the friction in the axle of the cylinder to be negligible, find the time dependence of
(a) the angular velocity of the cylinder and
(b) the kinetic energy of the whole system ( $M = 2 m$ ).

Video Solution

Text Solution

Verified by Experts

(a) Net force which is effective on the system (cylinder M+body m) is the weight of the body m in a uniform gravitational field, which is a constant. Thus the initial acceleration of the body m is also constant.
From the conservation of mechanical energy of the said system in the uniform field of gravity at time $t = Δ t : Δ T + Δ U = 0$
or $\frac{1}{2} m v^{2} + \frac{1}{2} \frac{M R^{2}}{2} ω^{2} - m g Δ h = 0$
or, $\frac{1}{2} (2 m + M) v^{2} - m g Δ h = 0$ [as $v = ω R$ at all times] (1)
But $v^{2} = 2 w Δ h$
Hence using it in Eq. (1), we get
$\frac{1}{4} (2 m + M) 2 w Δ h - m g Δ h = 0$ or $w = \frac{2 m g}{(2 m + M)}$
From the kinematical relationship, $β = \frac{w}{R} = \frac{2 m g}{(2 m + M) R}$
Thus the sought angular velocity of the cylinder
$ω (t) = β t = \frac{2 m g}{(2 m + M) R} t = \frac{g t}{(1 + M / 2 m) R}$
(b) Sought kinetic energy.
$T (t) = \frac{1}{2} m v^{2} + \frac{1}{2} \frac{M l^{2}}{2} ω^{2} = \frac{1}{4} (2 m + M) R^{2} ω^{2}$

Updated on:21/07/2023

Moment of inertia of a hollow cylinder of mass $M$ and radius $R$ , about the axis of cylinder is
A $\frac{1}{2} M R^{2}$
B $M R^{2}$
C $\frac{2}{3} M R^{2}$
D $\frac{2}{5} M R^{2}$
In the following figure, a body of mass m is tied at one end of a light string and this string is wrapped around the solid cylinder of mass M and radius R. At the moment t = 0 the system starts moving. If the friction is negligible, angular velocity at time t would be

A $\frac{m g R t}{(M + m)}$
B $\frac{2 M g t}{(M + 2 m)}$
C $\frac{2 m g t}{R (M - 2 m)}$
D $\frac{2 m g t}{R (M + 2 m)}$
A rope is wound round a hollow cylinder of mass M and radius R. If the rope is pulled with a force F newton, then the angular acceleration of the cylinder will be
A $M R F$
B $\frac{M R}{F}$
C $\frac{R}{M F}$
D $\frac{F}{M R}$