Determine the relationship between the torque N and the torsion angle φ for
(a) the tube whose wall thickness Δr is considerably less than the tube radius,
(b) for the solid rod of circular cross-section. Their lengh l, radius r, and shear modulus G are supposed to be known.
(a) Consider a hollow cylinder of length l, outer radius r+Δr inner radius r, fixed at one end and twisted at the other by means of a couple of moment N. The angular displacement φ, at a distance l from the fixed end, is proportional to both l and N. Consider an element of length dx at the twisted end. It is moved by an angle φ as shown. A vertical section is also shown and the twisting of the parallelopipe of length l and area Δrdx under the action of the twisting couple can be discussed by elementary means. If f is the tangential force generated then shearing stress is f/Δrdx and this must equal
Gθ=Grφl, since θ=rφl.
Hence, f=GΔrdxrφl.
The force f has moment fr about the axis and so the total moment is
N=GΔrφlr2∫dx=2πr3ΔrφlG
(b) For a solid cylinder we must integrate over r. Thus
N=0r∫2πr3drφGl=πr4Gφ2l

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics
25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
Maximum pressure difference between inner and outer surface of a thin walled circular tube of radius r and thickness Δr(Δr<<r) so that tube won't break is (Breaking stress of the material is σ0)
View SolutionTwo capillaries of small cross section are connected as shown in the figure. The right tube has cross sectional radius R and left one has a radius of r(<R). The tube of radius R is very long where as the tube of radius r is of short length. Water is slowly poured in the right tube. Contact angle for the tube wall and water is θ=0∘. Let h be the height difference between water surface in the right and left tube. Surface tension of water is T and its density is ρ.
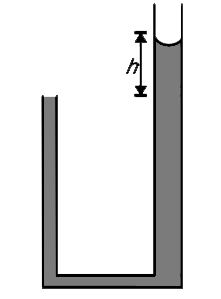
(a) Find the value of h if the water surface in the left tube is found to be flat.
(b) Find the maximum value of h for which water will not flow out of the left tube .
View Solution
Knowledge Check
Maximum pressure difference between inner and outer surface of a thin walled circular tube of radius r and thickness Δr(Δr<<r) so that tube won't break is (Breaking stress of the material is σ0)
Aσ0rΔrBΔrσ0rC2σ0rΔDσ0
A circular tube of mean radius 8cm and thickness 0.04cm is melted up and recast into a solid rod of the same length. The ratio of the torsional rigidities of the circular tube and the solid rod i
View SolutionSuppose N electrons can be placed in either of two configurations. In configuration 1, they are all placed on the circumference of a narrow ring of radius R and are uniformly distributed so that the distance between adjacent electrons is the same everywhere. In configuration 2, N - 1 electrons are uniformly distributed on the ring and one electron is placed in the center of the ring. (a) What is the smallest value of N for which the second configuration is less energetic than the first? (b) For that value of N, consider any one circumference electron-call it e0. How many other circumference electrons are closer to e0 than the central electron is ?
View SolutionA wedge of mass m and triangular cross- section (AB = BC = CA = 2R) is moving with a constant velocity −vˆI towards a sphere of radius R fixed on a smooth horizontal table as shown in figure. The wadge makes an elastic collision with the fixed sphere and returns along the same path without any rotaion. Neglect all friction and suppose that the wedge remains in contact with the sphere for a very shot time. Δt, during which the sphere exerts a constant force F on the wedge.
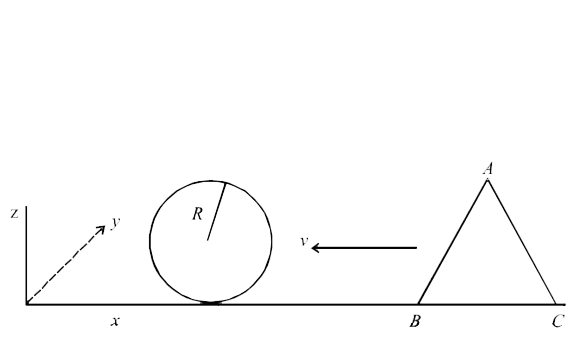
(a) Find the force F and also the normal force N exerted by the table on the wedge during the time Δt.
(b) Ler h denote the perpendicular distance between the centre of mass of the wedge and the line of action of F. Find the magnitude of the torque due to the normal force N about the centre of the wedge, during the interval Δt.
View SolutionA wedge of mass m and triangular cross- section (AB = BC = CA = 2R) is moving with a constant velocity −vˆI towards a sphere of radius R fixed on a smooth horizontal table as shown in figure. The wadge makes an elastic collision with the fixed sphere and returns along the same path without any rotaion. Neglect all friction and suppose that the wedge remains in contact with the sphere for a very shot time. Δt, during which the sphere exerts a constant force F on the wedge.

(a) Find the force F and also the normal force N exerted by the table on the wedge during the time Δt.
(b) Ler h denote the perpendicular distance between the centre of mass of the wedge and the line of action of F. Find the magnitude of the torque due to the normal force N about the centre of the wedge, during the interval Δt.
View SolutionThe Betatron was the first important machine for producing high energy electrons. The action of the betatron depends on the same fundamental principle as that of the transformer in which an alternating current applied to a primary coil induces an altermating current usually with higher or lower voltage in the secondary coil. In the betatron secondary coil is replaced by a doughnut shaped vacuum chamber.Electron produced in the doughnut from a hot filament, are given a preliminary acceleration by the application of an electric field having potential difference of 20kV to 70kV, when an alternating magnetic field is applied parallel to the axis of the tube, two effects are produced (1) an electromotive force is produced in the electron orbit by the changing magnetic flux that gives an additional energy to the electrons (2) a radial force is produced by the action of magnetic field whose direction is perpendicular to the electron velocity. Which keeps the electron moving in a circular path. Conditions are arranged such that the increasing magnetic field keeps the electron in a circular orbit of constant radius. The mathematical relation between the betatron parameters to ensure the above condition is called BETATRON condition.
If the orbit radius of the circular path traced by the electron is R, magnetic field is B, speed of the electron is v, mass of the electron is m, charge on the electron is e and ϕ is the flux within the orbit of radius R. Then answer the following questions based on the above comprehension.
What is the tangential force acting on the electron ?
View SolutionThe Betatron was the first important machine for producing high energy electrons. The action of the betatron depends on the same fundamental principle as that of the transformer in which an alternating current applied to a primary coil induces an altermating current usually with higher or lower voltage in the secondary coil. In the betatron secondary coil is replaced by a doughnut shaped vacuum chamber.Electron produced in the doughnut from a hot filament, are given a preliminary acceleration by the application of an electric field having potential difference of 20kV to 70kV, when an alternating magnetic field is applied parallel to the axis of the tube, two effects are produced (1) an electromotive force is produced in the electron orbit by the changing magnetic flux that gives an additional energy to the electrons (2) a radial force is produced by the action of magnetic field whose direction is perpendicular to the electron velocity. Which keeps the electron moving in a circular path. Conditions are arranged such that the increasing magnetic field keeps the electron in a circular orbit of constant radius. The mathematical relation between the betatron parameters to ensure the above condition is called BETATRON condition.
If the orbit radius of the circular path traced by the electron is R, magnetic field is B, speed of the electron is v, mass of the electron is m, charge on the electron is e and ϕ is the flux within the orbit of radius R. Then answer the following questions based on the above comprehension.
What is the BETATRON condition ?
View SolutionThe Betatron was the first important machine for producing high energy electrons. The action of the betatron depends on the same fundamental principle as that of the transformer in which an alternating current applied to a primary coil induces an altermating current usually with higher or lower voltage in the secondary coil. In the betatron secondary coil is replaced by a doughnut shaped vacuum chamber.Electron produced in the doughnut from a hot filament, are given a preliminary acceleration by the application of an electric field having potential difference of 20kV to 70kV, when an alternating magnetic field is applied parallel to the axis of the tube, two effects are produced (1) an electromotive force is produced in the electron orbit by the changing magnetic flux that gives an additional energy to the electrons (2) a radial force is produced by the action of magnetic field whose direction is perpendicular to the electron velocity. Which keeps the electron moving in a circular path. Conditions are arranged such that the increasing magnetic field keeps the electron in a circular orbit of constant radius. The mathematical relation between the betatron parameters to ensure the above condition is called BETATRON condition.
If the orbit radius of the circular path traced by the electron is R, magnetic field is B, speed of the electron is v, mass of the electron is m, charge on the electron is e and ϕ is the flux within the orbit of radius R. Then answer the following questions based on the above comprehension.
What is the value of d(m|→v|)dt ?
View Solution
