Find how the volume density of the elastic deformation energy is distributed in a steel rod depending on the distance r from its axis. The length of the rod is equal to l, the torsion angle to φ.
The energy between radii r and r+dr is, by differentiation, πr3drlGφ2
Its density is πr3dr2πrdrlGφ2l=12Gφ2r2l2
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics
25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
Find the volume density of the elastic deformation energy in fresh water at the depth of h=1000m.
View SolutionFind the elastic deformation energy of a steel rod whose one end is fixed and the other is twisted through an angle φ=6.0∘. The length of the rod is equal to l=1.0m, and the radius to r=10mm.
View Solution
Knowledge Check
Ratio of energy density of two steel rods is 1:4 when same mass is suspended from the rods. If length of both rods is same then ratio of diameter of rods will be.
A√2:1B1:√2C1:2D2:1A thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l3 from the end of the rod is instantaneously at rest just after the elastic collision?
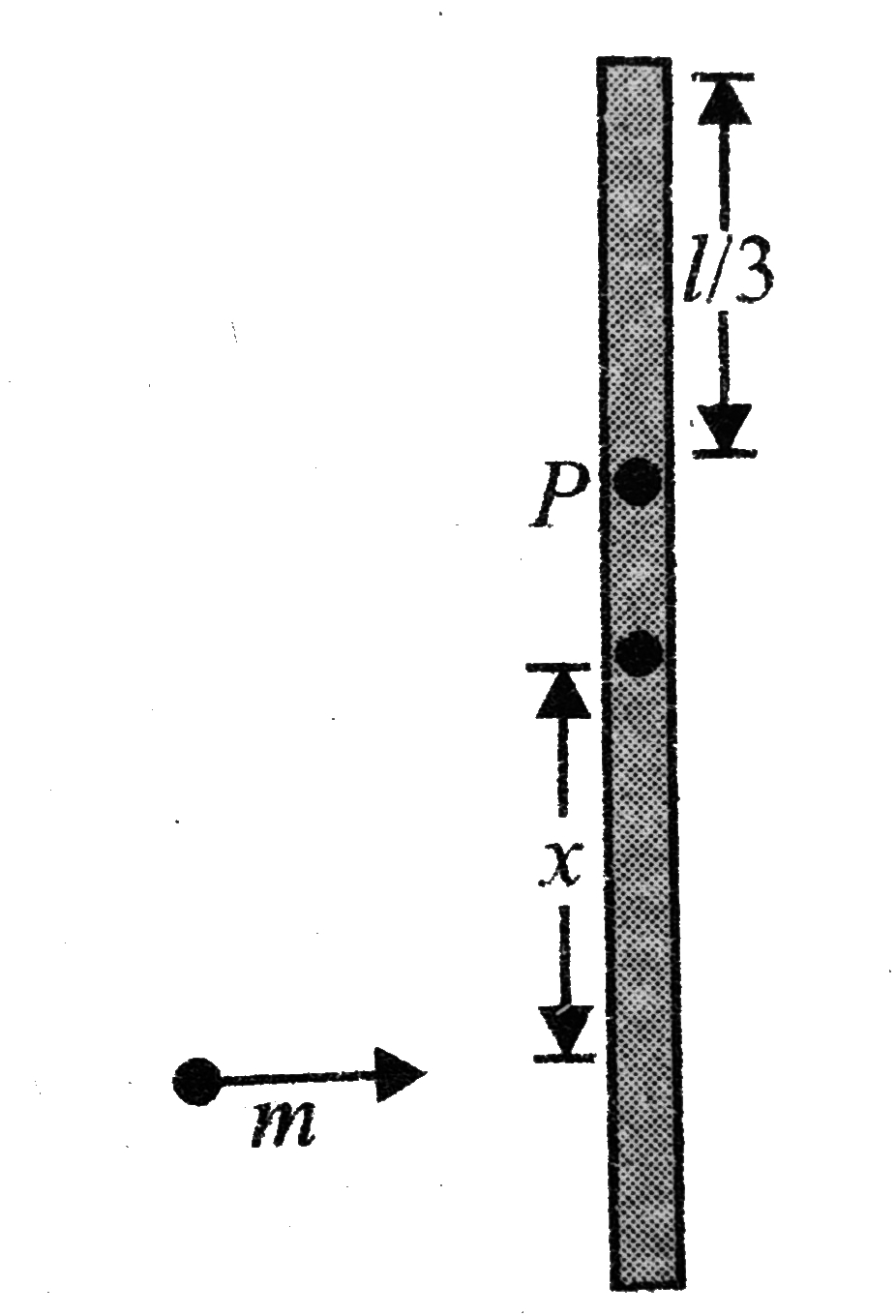 A1/2B1/3C1/6D1/4
A1/2B1/3C1/6D1/4Find centre of mass of given rod of linear mass density λ=(a+b(xl)2) , x is distance from one of its end. Length of the rod is l.
A3l4(3a+b2a+b)B3l4(2a+b3a+b)Cl4(2a+b3a+b)Dl(2a+b3a+b)
Find the elastic deformation energy of a steel rod of mass m=3.1kg stretched to a tensile strain ε=1.0⋅10−3.
View SolutionRatio of energy density of two steel rods is 1:4 when same mass is suspended from the rods. If length of both rods is same then ratio of diameter of rods will be.
View SolutionThe moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
View SolutionA thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l3 from the end of the rod is instantaneously at rest just after the elastic collision?

View SolutionFind centre of mass of given rod of linear mass density λ=(a+b(xl)2) , x is distance from one of its end. Length of the rod is l.
View Solution
