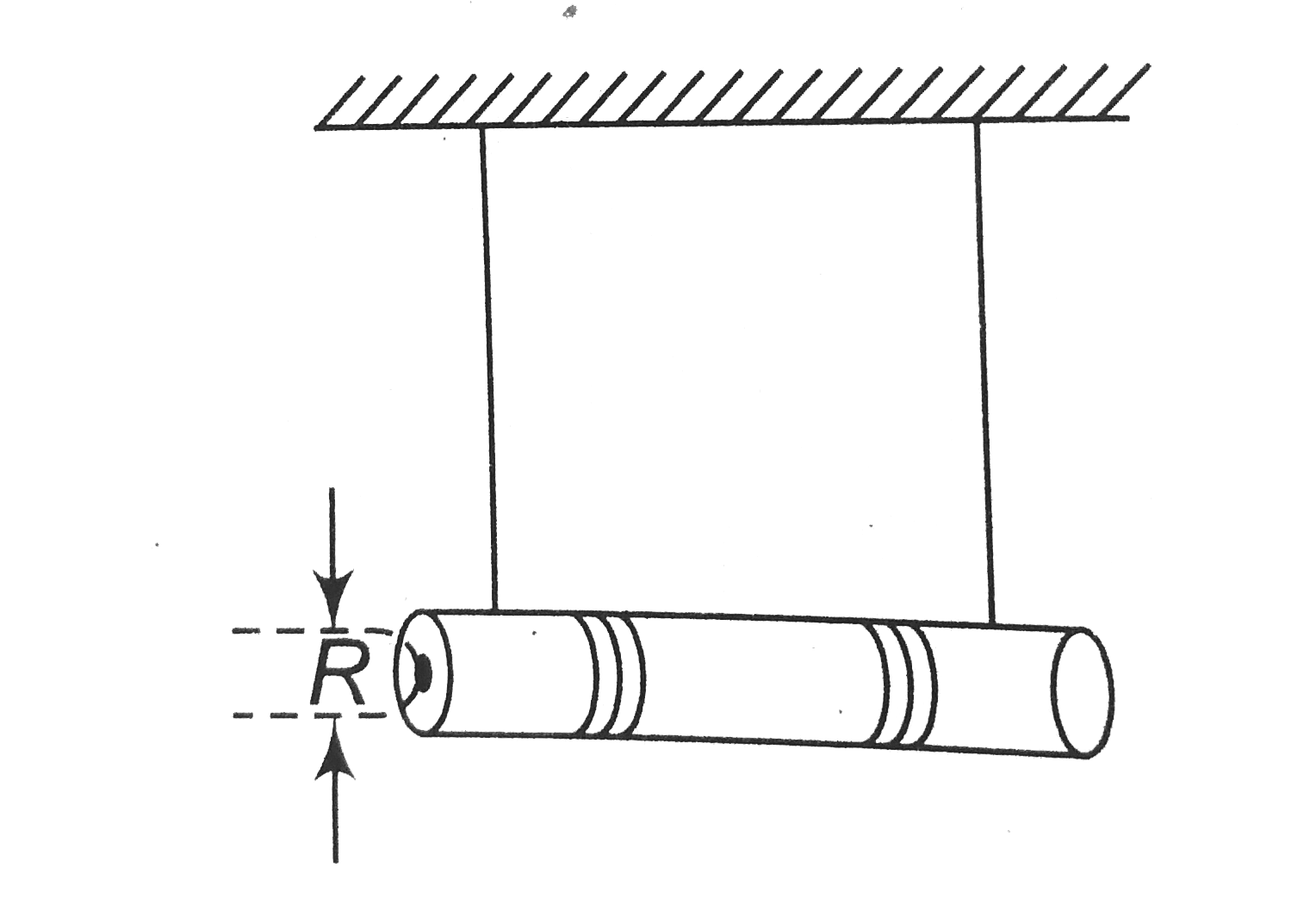
A steel cylindrical rod of length $l$ and radius $r$ is suspended by its end from the ceiling.
(a) Find the elastic deformation energy U of the rod.
(b) Define U in terms of tensile strain $Δ l / l$ of the rod.

Video Solution

Text Solution

Verified by Experts

When a rod is deformed by its own weight the stress increases as one moves up, the stretching force being the weight of the portion below the element considered.
The stress on the element $d x$ is
$ρ π r^{2} (l - x) g / π r^{2} = ρ g (l - x)$
The extension of the element is
$Δ d x = d Δ x = ρ g (l - x) d x / E$
Integrating $Δ l = \frac{1}{2} ρ g l^{2} / E$ is the extension of the whole rod. The elastic energy of the element is
$\frac{1}{2} ρ g (l - x) \frac{ρ g (l - x)}{E} π r^{2} d x$
Integrating
$Δ U = \frac{1}{6} π r^{2} ρ^{2} g^{2} l^{3} / E = \frac{2}{3} π r^{2} l E {(\frac{Δ l}{l})}^{2}$

Updated on:21/07/2023

There is a rod of length $l$ and mass $m$ . It is hinged at one end to the ceiling. The period of small oscillation is
A $T = 2 π \sqrt{\frac{2 l}{3 g}}$
B $T = π \sqrt{\frac{l}{3 g}}$
C $T = 2 π \sqrt{\frac{l}{3 g}}$
D $T = 2 π \sqrt{\frac{l}{g}}$
A uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
A $\frac{2}{3} π^{2} f^{2} m l^{2}$
B $\frac{4}{3} f^{2} m l^{2}$
C $4 π^{2} f^{2} m l^{2}$
Dzero
A uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
A $\frac{2}{3} π^{2} f^{2} m l^{2}$
B $\frac{4}{3} f^{2} m l^{2}$
C $4 π^{2} f^{2} m l^{2}$
DZero