A bar made of material whose Young's modulus is equal to E and Poisson's ratio to is subjected to the hydrostatic pressure p. Find:
(a) the fractional decrement of its volume,
(b) the relationship between the compressibility and the elastic constants E and .
Show that Poisson's ratio cannot exceed .
Consider a cube of unit length before pressure is applied. The pressure acts on each face. The pressure on the opposite faces constitute a tensile stress producing longitudinal compression and lateral extension. The compressions is and the lateral extension is
The net result is a compression
in each side.
Hence because from symmetry
(b) Let us consider a cube under an equal compressive stress , acting on all its faces.
Then, volume strain , (1)
where k is the bulk modulus of elasticity.
So
or, (as )
if E and are both to remain positive.
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics
25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
Consider a uniform wire of length l. Cross-sectional area A, Young's modulus of the material of the wave is Y. Some information related to the wire is given in column-1 and dependence of the result is given in column-2. Then match the approprite choice between the columns and match the list given in options
Column-I Column-II(A) Let us suspend wire vertically from a (p) Young'sModulusrigud support and attach a mass m atits lower end. If the mass is slightly pulleddown and released, it executes S.H.Mof a time period which will depend on(B) Work done in stretching the wire up to length (q) elongation (x)l+xwill depend on(C) If the given is fixed between two rigid (r) length (l)supports and its temperature is decreasedthermal stress that develops in the wirewill depend on(D) If the wire is pulled at its ends equal and (s) area of cross-section (A) opposite forces of magnitude F so that itundergoes an elongation x, according toHook's law, F=kx, where k is the forceconstant.Force constant (k) of the wirewill depend on
View SolutionConsider a uniform wire of length l. Cross-sectional area A, Young's modulus of the material of the wave is Y. Some information related to the wire is given in column-1 and dependence of the result is given in column-2. Then match the approprite choice between the columns and match the list given in options
Column-I Column-II(A) Let us suspend wire vertically from a (p) Young'sModulusrigud support and attach a mass m atits lower end. If the mass is slightly pulleddown and released, it executes S.H.Mof a time period which will depend on(B) Work done in stretching the wire up to length (q) elongation (x)l+xwill depend on(C) If the given is fixed between two rigid (r) length (l)supports and its temperature is decreasedthermal stress that develops in the wirewill depend on(D) If the wire is pulled at its ends equal and (s) area of cross-section (A) opposite forces of magnitude F so that itundergoes an elongation x, according toHook's law, F=kx, where k is the forceconstant.Force constant (k) of the wirewill depend on
View Solution
Knowledge Check
Le chatelier's principle
If a system at equilibrium is subjected to a change of any one of the factors such as concentration, pressure or temperature, the system adjusts itself in such a way so as to minimise the effect of that change. Change of pressure: If a system in equilibrium consists of gases, then the concentrations of all the components can be altered by changing the pressure.When the pressure on the system is increased, the volume decreases proportionately.The total number of moles per unit volume will now be more and the equilibrium will shift in the direction in which there is decrease in number of moles i.e., towards the direction in which there is decrease in volume.
Effect of pressure on melting point : There are two types of solids :
(a)Solids whose volume decreases on melting e.g. ice, diamond , carborundum, magnesium nitride and quartz.
Solid (higher volume)⇔ Liquid (lower volume)
The process of melting is facilitated at high pressure, thus melting point is lowered.
(b)Solids whose volume increase on melting, e.g. Fe,Cu, Ag,Au, etc.
Solid (lower volume)⇔ Liquid (higher volume)
In this case the process of melting becomes difficult at high pressure, then melting point becomes high.
(c )Solubility of subtances : When solid substance are dissolved in water, either heat is evolved (exothermic) or heat is absorbed (endothermic).
KCl+aq⇔KCl(aq)-heat
In such cases,solubility increase with increase in temperature.
Consider the case of KOH, when this is dissolved heat is evolved.
KOH+aq⇔KOH(aq)+heat
In such cases, solubility decrease with increase in temperature.
(d)Solubility of gases in liquids : When a gas dissolves in liquid, there is decreases in volume. Thus, increases of pressure will favour the dissolution of gas in liquid.
Effect of temperature: Le-Chatelier's principle predicts a system at equilibrium will tend to shift in the endothermic direction when temperature is raised, for then energy is absorbed as heat and the rise in temperature is opposed.Conversely, an equilibrium will shift in the exothermic direction if the temperature is lowered, for then energy is released and the reduction in temperture is opposed Van't Hoff equation shows the dependence of equilibrium constant K on temperaure as :
ddTlnK=ΔH∘RT2orlnK=constant−ΔH∘R.1T
Au(s)⇔Au(l)AHigh pressure, low temperatureBHigh pressure, high temperatureCLow pressure, high temperatureDLow pressure, low temperatureLe chatelier's principle
If a system at equilibrium is subjected to a change of any one of the factors such as concentration, pressure or temperature, the system adjusts itself in such a way so as to minimise the effect of that change. Change of pressure: If a system in equilibrium consists of gases, then the concentrations of all the components can be altered by changing the pressure.When the pressure on the system is increased, the volume decreases proportionately.The total number of moles per unit volume will now be more and the equilibrium will shift in the direction in which there is decrease in number of moles i.e., towards the direction in which there is decrease in volume.
Effect of pressure on melting point : There are two types of solids :
(a)Solids whose volume decreases on melting e.g. ice, diamond , carborundum, magnesium nitride and quartz.
Solid (higher volume)⇔ Liquid (lower volume)
The process of melting is facilitated at high pressure, thus melting point is lowered.
(b)Solids whose volume increase on melting, e.g. Fe,Cu, Ag,Au, etc.
Solid (lower volume)⇔ Liquid (higher volume)
In this case the process of melting becomes difficult at high pressure, then melting point becomes high.
(c )Solubility of subtances : When solid substance are dissolved in water, either heat is evolved (exothermic) or heat is absorbed (endothermic).
KCl+aq⇔KCl(aq)-heat
In such cases,solubility increase with increase in temperature.
Consider the case of KOH, when this is dissolved heat is evolved.
KOH+aq⇔KOH(aq)+heat
In such cases, solubility decrease with increase in temperature.
(d)Solubility of gases in liquids : When a gas dissolves in liquid, there is decreases in volume. Thus, increases of pressure will favour the dissolution of gas in liquid.
Effect of temperature: Le-Chatelier's principle predicts a system at equilibrium will tend to shift in the endothermic direction when temperature is raised, for then energy is absorbed as heat and the rise in temperature is opposed.Conversely, an equilibrium will shift in the exothermic direction if the temperature is lowered, for then energy is released and the reduction in temperture is opposed Van't Hoff equation shows the dependence of equilibrium constant K on temperaure as :
ddTlnK=ΔH∘RT2orlnK=constant−ΔH∘R.1T
For the reaction 12N2(g)+12O2(g)⇔NO(g)ATotal pressure at equilibrium will changeBConcentration of all the component at equilibrium will not changeCConcentration of all the component at equilibrium will remain sameDEquilibrium will shift in the forward directionLe chatelier's principle
If a system at equilibrium is subjected to a change of any one of the factors such as concentration, pressure or temperature, the system adjusts itself in such a way so as to minimise the effect of that change. Change of pressure: If a system in equilibrium consists of gases, then the concentrations of all the components can be altered by changing the pressure.When the pressure on the system is increased, the volume decreases proportionately.The total number of moles per unit volume will now be more and the equilibrium will shift in the direction in which there is decrease in number of moles i.e., towards the direction in which there is decrease in volume.
Effect of pressure on melting point : There are two types of solids :
(a)Solids whose volume decreases on melting e.g. ice, diamond , carborundum, magnesium nitride and quartz.
Solid (higher volume)⇔ Liquid (lower volume)
The process of melting is facilitated at high pressure, thus melting point is lowered.
(b)Solids whose volume increase on melting, e.g. Fe,Cu, Ag,Au, etc.
Solid (lower volume)⇔ Liquid (higher volume)
In this case the process of melting becomes difficult at high pressure, then melting point becomes high.
(c )Solubility of subtances : When solid substance are dissolved in water, either heat is evolved (exothermic) or heat is absorbed (endothermic).
KCl+aq⇔KCl(aq)-heat
In such cases,solubility increase with increase in temperature.
Consider the case of KOH, when this is dissolved heat is evolved.
KOH+aq⇔KOH(aq)+heat
In such cases, solubility decrease with increase in temperature.
(d)Solubility of gases in liquids : When a gas dissolves in liquid, there is decreases in volume. Thus, increases of pressure will favour the dissolution of gas in liquid.
Effect of temperature: Le-Chatelier's principle predicts a system at equilibrium will tend to shift in the endothermic direction when temperature is raised, for then energy is absorbed as heat and the rise in temperature is opposed.Conversely, an equilibrium will shift in the exothermic direction if the temperature is lowered, for then energy is released and the reduction in temperture is opposed Van't Hoff equation shows the dependence of equilibrium constant K on temperaure as :
ddTlnK=ΔH∘RT2orlnK=constant−ΔH∘R.1T
The plot of log K against 1T is a straight line with positive slope ( K being the equilibrium constant of a reaction ), which of the following is then correct ?AThe reaction is endothermic in natureBThe reaction willl be exothermic in natureCThe reaction goes to farther extent on raising the temperatureDNone of these
1 liter of an ideal gas (γ=1.5) at 300k is suddenly compressed to half its original volume. (a) Find the ratio of the final pressure to the initial pressure. (b) If the original pressure is 100kpa, find the work done by the gas in the process. (c) What is the change in internal energy? (d) What is the final temperature? (e) the gas is now colled to 300k keeping its pressure constant. Calculate the work done during the process . (f) The gas is now expanded iasothermally to achive its original volume of 1 liters. Calculate the work done by the gas .(g) Calculate the total work done in the cycle.
View SolutionConsider two coherent sources S1andS2 producing monochromatic waves to produce interference patten. Let the displacement of the wave produced by S1 be given by
and the displacement by S2 be Y1=acosωt
Y2=acos(ωt−ϕ)
Find out expression for the amplitude of the resultant displacement at a point and show that the intensity at that point will be
I=4a2cos2ϕ/2
Hence establish the conditions for constructive and destructive interference.
(b) What is the effect on the interference friinges in Young's double slit experiment when (i) the width of the source slit is increased, (ii) the monochromatic source is replaced by a source is replaced by a source of white light ?
OR
(a) A ray, 'PQ' of light on the face AB of glass prism ABC (as shown in the figure) and emerges out of the face AC. Trace the path of the ray. Show that
∠i+∠e=∠A+∠δ
Where δ and e denote the angle of deviation and angle of emergence respectively.
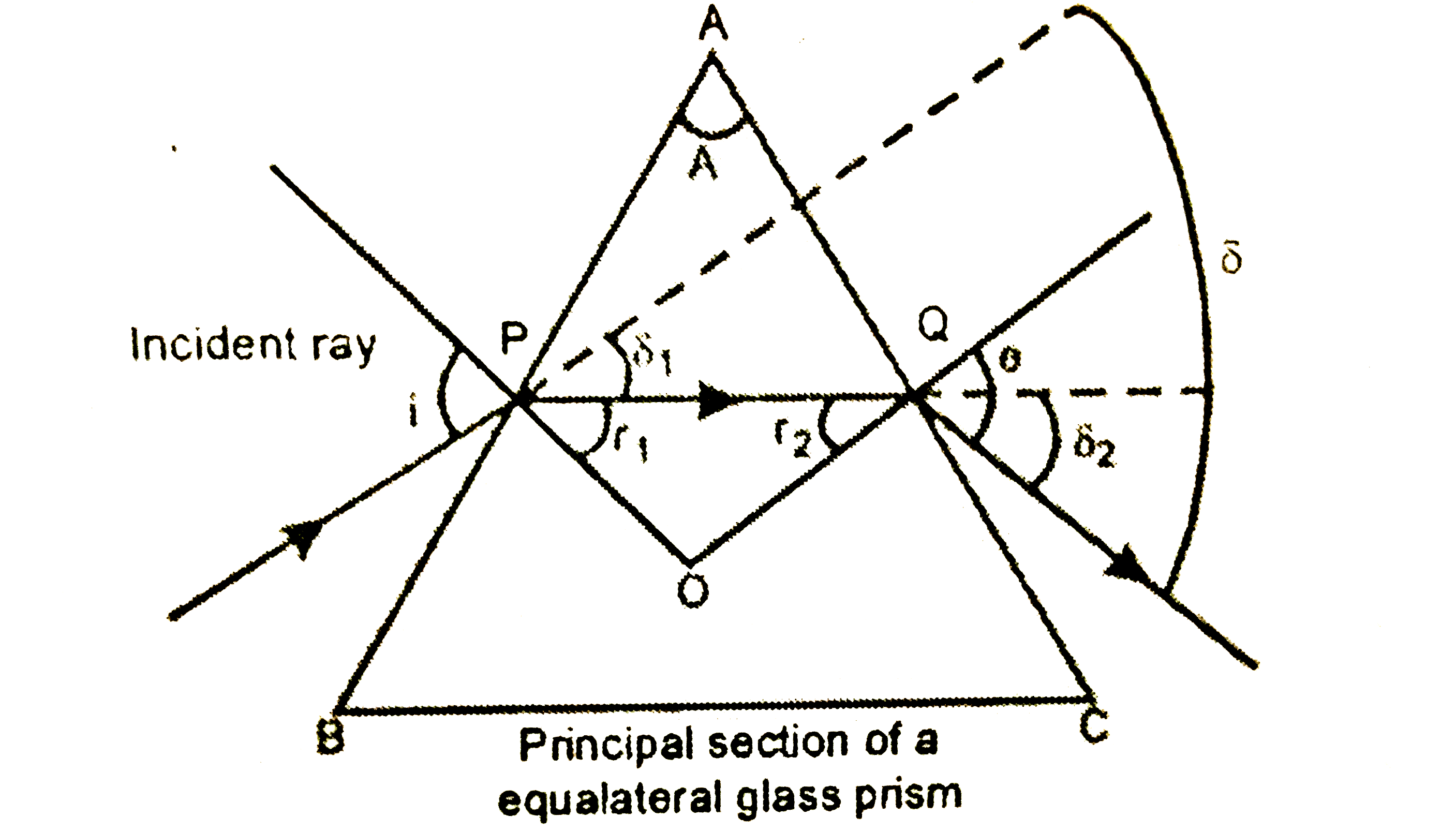
Plot a graph showing the variation of the angle of deviation as a function of angle of incidence. state the condition under which ∠δ is minimum.
(b) Find out the relation between the refractive index (μ) of the glass prism and ∠A for the case when the angle of prism (A) is equal to the angle of minimum deviation (δm) . Hence obtain the value of the refractive index for angle Ae=60∘ .
View SolutionA rigid cylindrical container has inner radius r. A cork having radius r+Δr and length L is to be fitted so as to close the container. Uniform pressure (ΔP) is needed on the curved cylindrical surface of the cork. Poisson’s ratio of a cork is almost zero, and its bulk modulus is B.
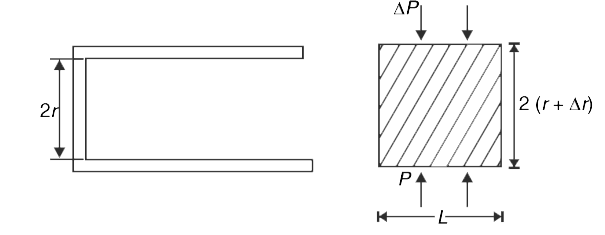
(a) Calculate ΔP
(b) After the cork is fitted how much force will be needed to pull it out of the container? Coefficient of friction between the container and the cork is μ.
View SolutionRotational energy levels of diatomic molecules are well described by the formula EJ=BJ(J+1), where J is the rotational quantum number of the molecule and B its rotational constant. B is related to the reduced
mass μ and the bond length R of the molecule through the equation B=h28π2μR2.
In general, spectroscopic transitions appear at photon energies which are equal to the energy difference between appropriate states of a molecule (hv=ΔE). The observed rotational transitions occur between adjacent rotational levels, hence ΔE=EJ+1−EJ=2B(J+1). Consequently, successive rotational transitions that appear on the spectrum (such as the one shown here) follow the equation h(Δυ)=2B.
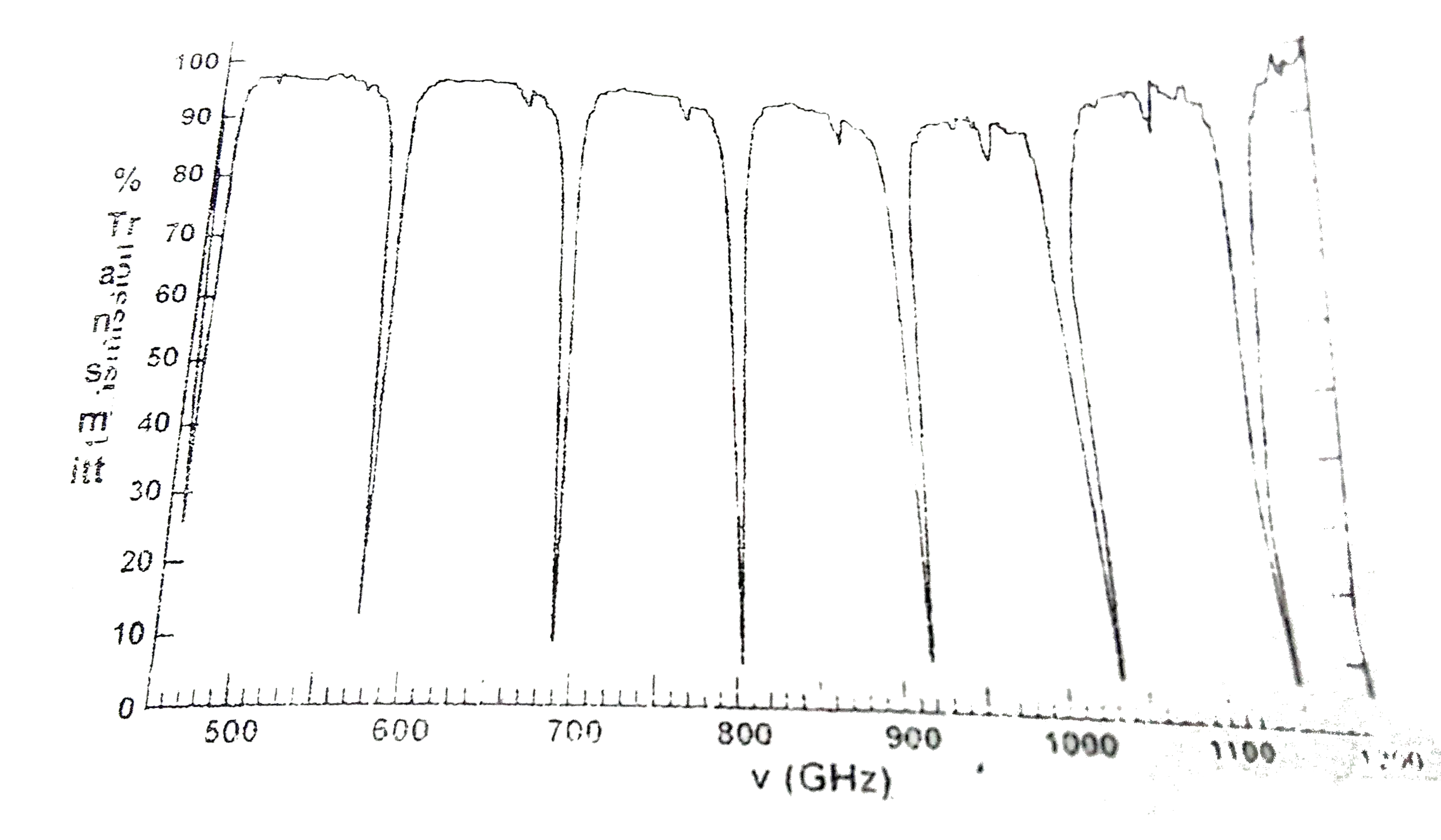
By inspecting the spectrum provided, determine the following quantities for ^(2)C^(p)Cwithap∝riateunits<br>(a)Deltaupsilon(b)B(c)R
View SolutionRotational energy levels of diatomic molecules are well described by the formula EJ=BJ(J+1), where J is the rotational quantum number of the molecule and B its rotational constant. B is related to the reduced
mass μ and the bond length R of the molecule through the equation B=h28π2μR2.
In general, spectroscopic transitions appear at photon energies which are equal to the energy difference between appropriate states of a molecule (hv=ΔE). The observed rotational transitions occur between adjacent rotational levels, hence ΔE=EJ+1−EJ=2B(J+1). Consequently, successive rotational transitions that appear on the spectrum (such as the one shown here) follow the equation h(Δυ)=2B.

By inspecting the spectrum provided, determine the following quantities for ^(2)CpC with appropriate units
(a) Δυ (b) B (c) R
View Solution
