A steel girder of length l rests freely on two supports (figure). The moment of inertia of its cross-section is equal to I (see the foregoing problem). Neglecting the mass of the girder and assuming the sagging to be slight, find the deflection λ due to the force F applied to the middle of the girder.

One can think of it as analogous to the previous case but with a beam of length l/2 loaded upward by a force F/2.
Thus λ=Fl348EI,
On using the last result of the previous problem.

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics25videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics49videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body56videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
The bending of an elastic rod is described by the elastic curve passing through centres of gravity of rod's cross-sections. At small bendings the equation of this curve takes the form
N(x)=EId2ydx2,
where N(x) is the bending moment of the elastic forces in the cross-section corresponding to the x coordinate, E is Young's modulus, I is the moment of inertia of the cross-section relative to the axis pasing through the neutral layer (I=∫z2dS, figure)

Suppose one end of a steel rod of a square cross-section with side a is embedded into a wall, the protruding section being of length l (figure). Assuming the mass of the rod to be negligible, find the shape of the elastic curve and the deflection of the rod λ, if its end A experiences
(a) the bending moment of the couple N0, ,
(b) a force F oriented along the y axis.
 View Solution
View SolutionA smooth rod of length l rotates freely in a horizontal plane with the angular velocity about a stationary vertical axis O as shown in Fig. The moment of inertia of the rod is equal to I relative to the axis. A small ring of mass m is located on the rod close to the rotation axis and is tied to it by a thread. When the thread is burned, the ring starts sliding radially outwards along the rod. Find the velocity v of the ring relative to the rod as a function of its distance r from the rotation axis.
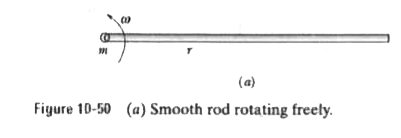 View Solution
View Solution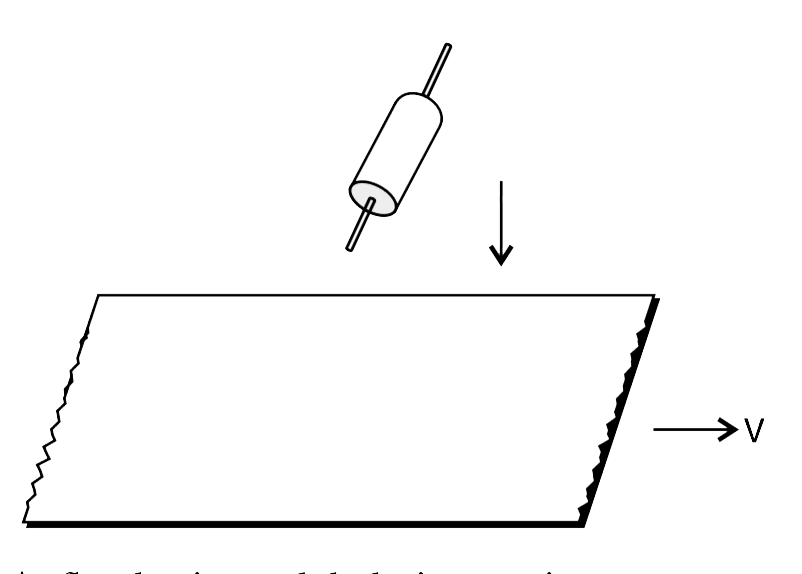
A flat horizontal belt is running at a constant speed V. There is a uniform solid cylinder of mass M which can rotate freely about an axle passing through its centre and parallel to its length. Holding the axle parallel to the width of the belt, the cylinder is lowered on to the belt. The cylinder begins to rotate about its axle and eventually stops slipping. The cylinder is, however, not allowed to move forward by keeping its axle fixed. Assume that the moment of inertia of the cylinder about its axle is 12MR2 where M is its mass and R its radius and also assume that the belt continues to move at constant speed. No vertical force is applied on the axle of the cylinder while holding it.
(a) Calculate the extra power that the motor driving the belt has to spend while the cylinder gains rotational speed. Assume coefficient of friction =μ.
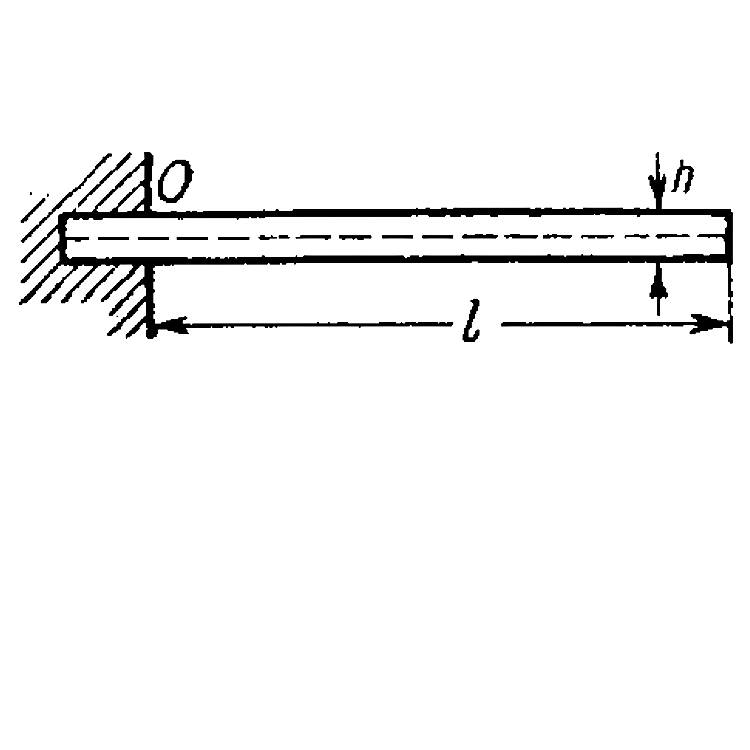
(b) Prove that 50% of the extra work done by the motor after the cylinder is placed over it, is dissipated as heat due to friction between the belt and the cylinderView SolutionOne end of a steel rectangular girder is embedded into a wall (figure). Due to gravity it sags slightly. Find the radius of curvature of the neutral layer (see the dotted line in the figure) in the vicinity of the point O if the length of the protruding section of the girder is equal to l=6.0m and the thickness of the girder equals h=10cm.
 View Solution
View SolutionA top of mass m=0.50kg, whose axis is tilted by an angle θ=30∘ to the vertical, precesses due to gravity. The moment of inertia of the top relative to its symmetry axis is equal to I=2.0g⋅m2, the angular velocity of rotation about that axis is equal to ω=350rad/s, the distance from the point of rest to the centre of inertia of the top is l=10cm. Find:
(a) the angular velocity of the top's precession,
(b) the magnitude and direction of the horizontal component of the reaction force acting on the top at the point of rest.View SolutionA spool with thread wound on it, of mass m, rests on a rough horizontal surface. Its moment of inertia relative to its own axis is equal to I=γmR2, where γ is a numerical factor, and R is the outside radius of the spool. The radius of the wound thread layer is equal to r. The spool is pulled without sliding by the thread with a constant force F directed at an angle α to the horizontal (figure). Find:
(a) the projection of the acceleration vector of the spool axis on the x-axis,
(b) the work performed by the force F during the first t seconds after the beginning of motion.
 View Solution
View SolutionA wedge of mass m and triangular cross- section (AB = BC = CA = 2R) is moving with a constant velocity −vˆI towards a sphere of radius R fixed on a smooth horizontal table as shown in figure. The wadge makes an elastic collision with the fixed sphere and returns along the same path without any rotaion. Neglect all friction and suppose that the wedge remains in contact with the sphere for a very shot time. Δt, during which the sphere exerts a constant force F on the wedge.
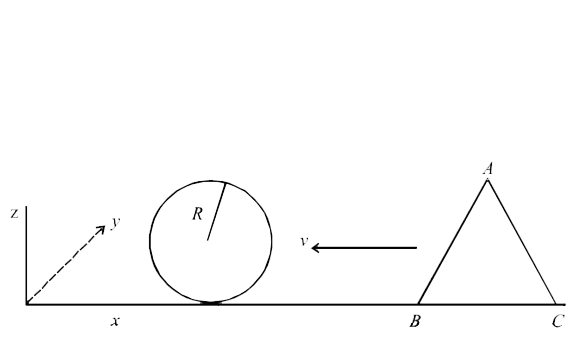
(a) Find the force F and also the normal force N exerted by the table on the wedge during the time Δt.
(b) Ler h denote the perpendicular distance between the centre of mass of the wedge and the line of action of F. Find the magnitude of the torque due to the normal force N about the centre of the wedge, during the interval Δt.View SolutionA wedge of mass m and triangular cross- section (AB = BC = CA = 2R) is moving with a constant velocity −vˆI towards a sphere of radius R fixed on a smooth horizontal table as shown in figure. The wadge makes an elastic collision with the fixed sphere and returns along the same path without any rotaion. Neglect all friction and suppose that the wedge remains in contact with the sphere for a very shot time. Δt, during which the sphere exerts a constant force F on the wedge.

(a) Find the force F and also the normal force N exerted by the table on the wedge during the time Δt.
(b) Ler h denote the perpendicular distance between the centre of mass of the wedge and the line of action of F. Find the magnitude of the torque due to the normal force N about the centre of the wedge, during the interval Δt.View SolutionTwo ends of an inductor of inductance L is connected to two parallel conducting rails. A conducting wire of length (that is equal to separation between the rails) can slide on the rails without friction. The wire has mass m. It is projected with a velocity v0 parallel to the rails (see Figure). Neglect self inductance and resistance of the loop.
(a) Find velocity of the wire as a function of time.
(b) Write current through the wire at time t.
(c) Find speed of the wire as a function of its displacement.
(d) Is the current in the conductor zero when it stops? If no, find this current .
(e) Will the conductor move after it stops?
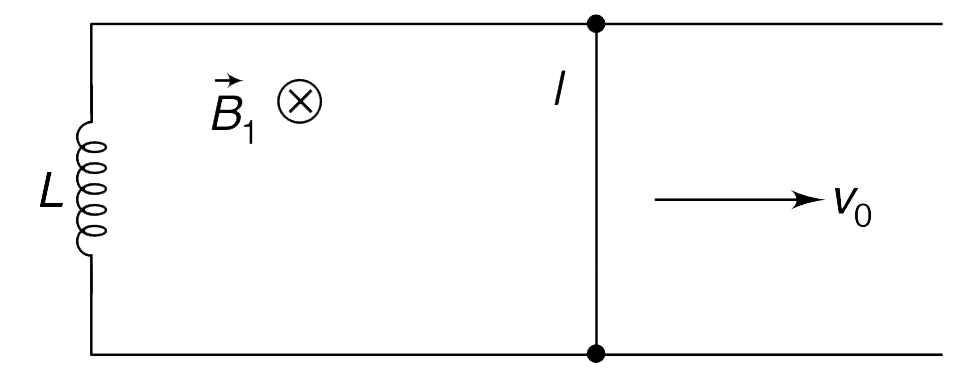 View Solution
View SolutionTwo long parallel horizontal rails a, a distance d aprt and each having a risistance λ per unit length are joing at one end by a resistance R. A perfectly conduction rod MN of mass m is free to slide along the rails without friction (see figure). There is a uniform magnetic field of induction B normal to the plane of the paper and directed into the paper. A variable force F is applied to the rod MN such that, as the rod moves a constant current flows through R.
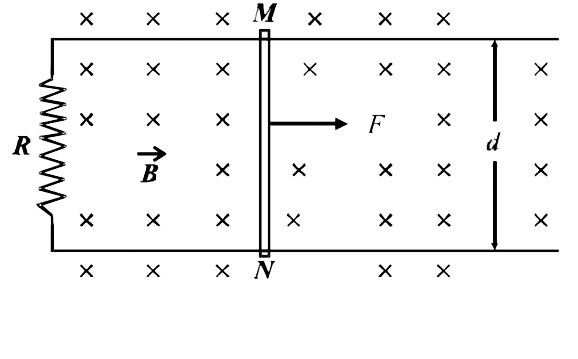
(i) Find the velocity of the rod and the applied force F as function of the distance x of the rod from R.
(ii) What fraction of the work done per second by F is converted into heat?View Solution

