In a traingle the proper length of each side equals a. Find the perimeter of this triangle in the reference frame moving relative to it with a constant velocity along one of its
(a) bisectors, (b) sides.
Investigate the results obtained at and , where c is the velocity of light.
(a) In the frame in which the traingle is at rest the space coordinates of the vertices are , , all measured at the same time t. In the moving frame the corresponding coordinates at time are
and
The perimeter P is then
(b) The coordinates in the first frame are shown at time t. The coordinates in the moving frame are,

The perimeter P is then
here
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics
25 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
A plane wave ζ=Acos(ωt−kx) propagates in the reference frame S. find the equation of this wave in a refreence frame S' moving in the +ve direction of x-axis with a constant velocity V relative to S.
View SolutionAn isosceles triangle has perimeter 30 cm and each of the equal sides of 12 cm. Find the area of the triangle.
View SolutionAn isosceles triangle has perimeter 30cm and each of the equal sides os 12 cm. Find the area of the triangle.
View SolutionThe lengths of the sides of a triangle are in the ration 3:4:5 and its perimeter is 144cm. Find the area of the triangle and the height corresponding to the longest side.
View SolutionLet a≤b≤c be the lengths of the sides of a triangle. If a2+b2<c2, then prove that triangle is obtuse angled .
View SolutionThe rod AB oriented parallel to the x′ axis of the reference frame K′ moves in this frame with a velocity v′ along its y′ axis. In its turn, the frame K′ moves with a velocity V relative to the frame K as shown in figure. Find the angle θ between the rod and the x axis in the frame K.

View SolutionFind the proper length of a rod if in the laboratory frame of reference its velocity is v=c/2, the length l=1.00m, and the angle between the rod and its direction of motion is θ=45∘.
View SolutionThe velocity components of a particle moving in the xy plane of the reference frame K are equal to vx and vy. Find the velocity v′ of this particle in the frame K in the positive direction of its x axis.
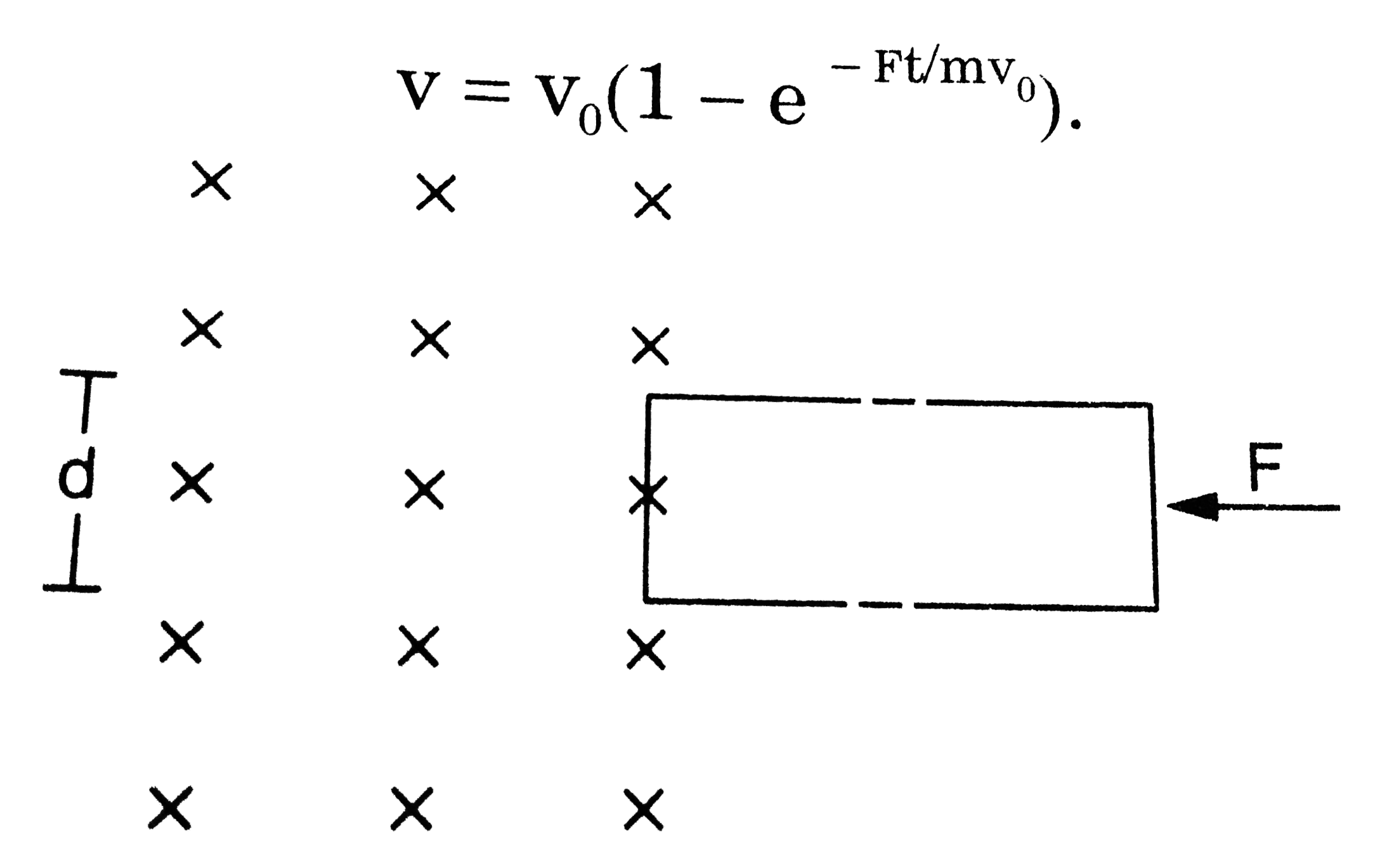
View SolutionThe rectangualr wire- frame, shown in has a width d, mass m, resistance R and a large length. A uniform magnetic field B exists to the left of the frame. A constant force F starts pushing the frame into the magnetic field at t =0. (a) Find the acceleration of the frame when its speed has increased to v. (b) Show that after some time the frame will move with a constant velocity till the whole frame enters into the magnetic field. find this velocity v0. (c) show that the velocity at tiem t is given by v=v0(1−e−Ftmv0.
View SolutionThe frame K′ moves with a constant velocity V relative to the frame K. Find the acceleration w′ of a particle in the frame K′, if in the frame K this particle moves with a velocity v and acceleration w along a straight line
(a) in the direction of the vector V,
(b) perpendicular to the vector V.
View Solution
