Find the proper length of a rod if in the laboratory frame of reference its velocity is v=c/2, the length l=1.00m, and the angle between the rod and its direction of motion is θ=45∘.
In the rest frame, the coordinates of the ends of the rod in terms of proper length l0
A:(0,0,0)B:(l0cosθ0,l0sinθ0,0)
at time t. In the laboratory frame the coordinates at time t' are
A:(vt′,0,0),B:(l0cosθ0srqt(1−β2)+vt',l0sinθ0,0)
Therefore we can write,
locsθ0=l0cosθ0√1−β2 and lsinθ=l0sinθ0
Hence l20=(l2)(cos2θ+(1−β2)sin2θ1−β2)
or, =√1−β2sin2θ1−β2

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics
25 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
Two rods having the same proper length l0 move lengthwise toward each other parallel to a common axis with the same velocity v relative to the laboratory frame of reference. What is the length of each rod in the reference frame fixed to the other rod?
View SolutionThe rod AB oriented parallel to the x′ axis of the reference frame K′ moves in this frame with a velocity v′ along its y′ axis. In its turn, the frame K′ moves with a velocity V relative to the frame K as shown in figure. Find the angle θ between the rod and the x axis in the frame K.

View SolutionA rod AB oriented along the x axis of the reference frame K moves in the positive direction of the x axis with a constant velocity v. The point A is the forward end of the rod, and the point B its near end. Find:
(a) the proper length of the rod, if at the moment tA the coorniate of the point A is equal to xA, and at the moment tB the coordinate of the point B is equal to xB,
(b) what time interval should separate the markings of coordinates of the rod's ends in the frame K for the difference of coordinates to become equal to the proper length of the rod.
View SolutionTwo rods of the same proper length l0 move toward each other parallel to a common horizontal axis. In the reference frame fixed to one of the rods the time interval between the moments, when the right and left ends of the rods coincide, is equal to Δt. What is the velocity of one rod relative to the other?
View SolutionA rod moves along a ruler with a constant velocity. When the positions of both ends of the rod are marked simultaneously in the reference frame fixed to the rule, the difference of readings on the rule is equal to Δx1=4.0m. But when the positions of the rod's ends are marked simultaneously in the reference frame fixed to the rod, the difference of readings on the same ruler is equal to Δx2=9.0m. Find the proper length of the rod and its velocity relative to the ruler.
View SolutionA conical pendulum, a thin uniform rod of length l and mass m, rotates uniformly about a vertical axis with angular velocity ω(the upper end of the rod is hinged). Find the angle θ between the rod and the vertical.
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View Solution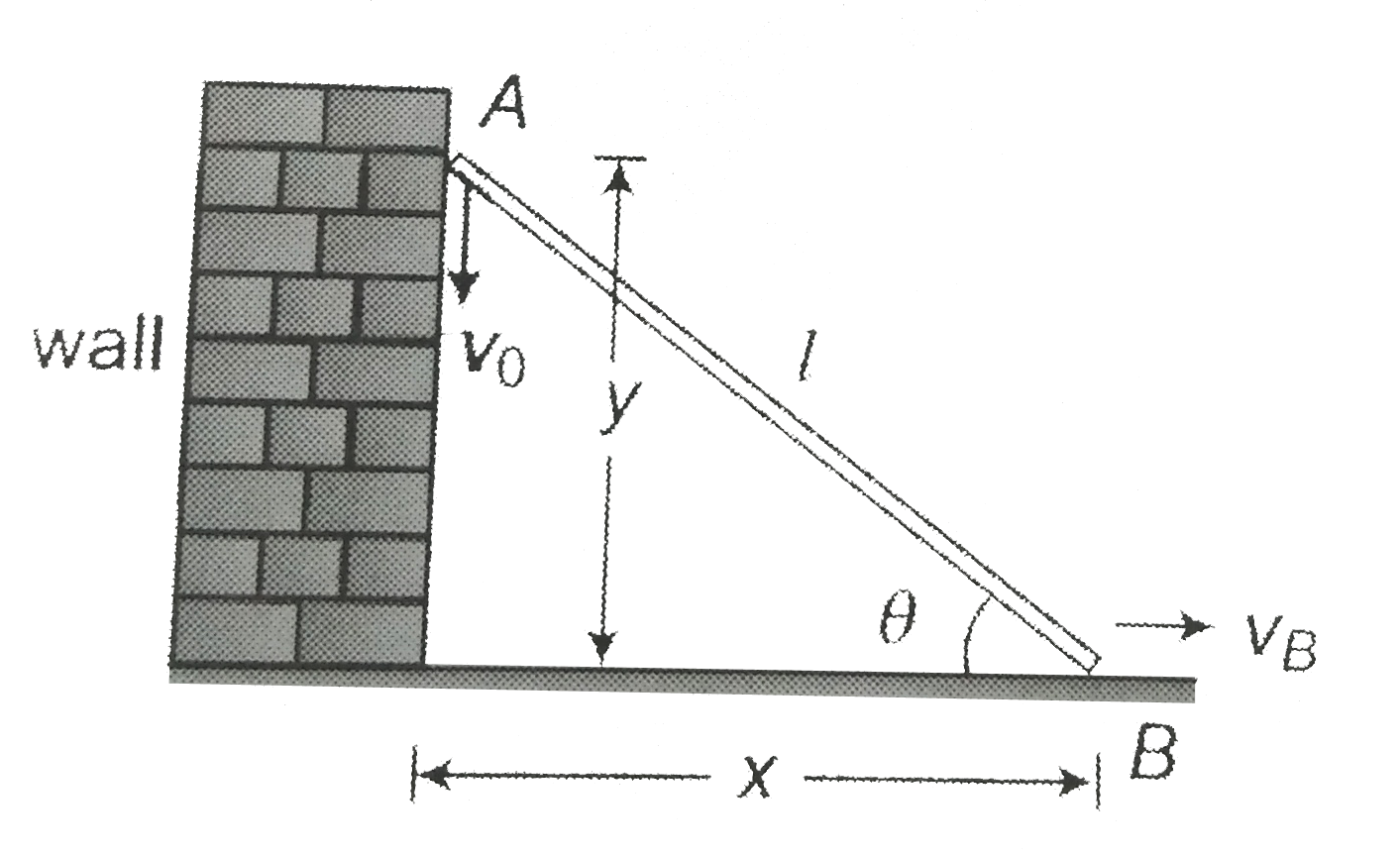
Consider a rod of length l resting on a wall and the floor. If the velocity of the upper end of a rod A is v0 in downward direction, find the velocity of the lower end B at this iinstant, when the rod makes an angle θ with horizontal
View SolutionA uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?

View Solution
