Doubtnut Promotions Sticky

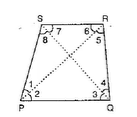
PQRS is a cyclic quadrilateral such that PR is a diameter of the circle. If ∠QPR=67∘and∠SPR=72∘, then ∠QRS=
(a)41∘ (b) 23∘ (c) 67∘ (d) 18∘

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

Angle in a semicircle is 90∘
Thus ∠PQR=∠PSR=90∘
∠QPS=∠QPR+∠RPS=67∘+72∘=139∘
Sum of all angles of quadrilateral must be 360∘
Thus, 90∘+90∘+139∘+∠QRS=360∘
∠QRS=41∘

|
Updated on:21/07/2023
Class 9MATHSCIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    If P:Q=2:3,Q:R=5:7andR:S=3:10 then P : S = ?

    A1:5
    B1:7
    C3:2
    D6:15
  • Question 2 - Select One

    If P is the husband of Q and R is the mother of S and Q, what is R to P?

    A(a) Mother
    B(b) Sister
    C(c) Aunt
    D(d) Mother-in-law
  • Question 3 - Select One

    P is Q's brother. R is Q's mother. S is R's father. T is S's mother. How is P related to T?
    P, Q का भाई है। R, Q की माता है। S, R का पिता है। T, S की माता है। P, T से किस प्रकार संबंधित है?

    AGranddaughter (पोती)
    BGreat grandson (परपोता)
    CGrandson (पोता)
    DGrandmother (दादी)