
Liquid of density ρ is filled in the container of negligible mass having area A. Area of hole 'a' is very small (a<<A). Co-efficient of friction between container and surface is equal to (aA). As liquid is coming out of vessel, instantaneous acceleration of the container.
(Aag)
3g2
(agA)
zero
The correct Answer is:C
At any time
Fthrust−Ffrictional=ma
ρav2−μmg=ma
ρa(2gh)−(aA)(ρAh)g=(ρAh)a'
2ρagh−ρagh=ρAha',aAg=a'
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)20videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)5videos
WORK, ENERGY AND POWER
Similar Questions
A container contains an incompressible and non - viscous liquid of density ρ and is filled upto a height H . Now if container is moved towards right with an acceleration a then find the horizontal force exerted by liquid on the face ABCD of container . Assume container have enough height so that liquid does not fall outside the container .
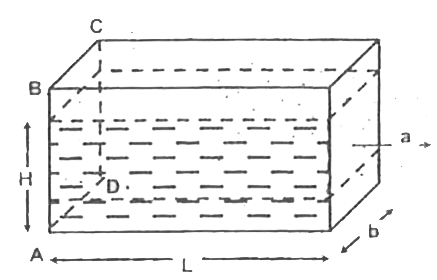 View Solution
View SolutionIf the pin hole in the container is very small compared to the area of the base of container and a block floats in the ideal liquid then, the speed of efflux is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Liquid of density ρ in a container exerts pressure P given by (height of liquid h and area A)
AP=AhρgBp=hρgCP=hρgADP=ρgAh - Question 2 - Select One
A solid cube floats in a liquid of density ρ with half of its volume submerged as shown. The side length of the cube is a, which is very small compared to the size of the container. Now a liquid of density ρ3 (immiscible with the liquid already in the container) is poured slowly into the container. The column of the liquid of density ρ3 that must be poured so that the cube is fully submerged (with its top surface coincident with the surface of the poured liquid) is :
 Aa3Ba2C2a3D3a4
Aa3Ba2C2a3D3a4 - Question 3 - Select One

A container is partially filled with a liquid of density ρ2 A capillary tube of radius r is vertically inserted in this liquid. Now another liquid of density ρ1(ρ1<ρ2) is slowly poured in the container to a height h as shown. There is only denser liquid in the capillary tube. The rise of denser liquid in the capillary tube is also h. Assuming zero contact angle, the surface tension of heavier liquid isArρ2ghB2πrρ2ghCr2(ρ2−ρ1)ghD2πr(ρ2−ρ1)gh
Liquid pressure is__________of the area and the shape of the containing vessel.
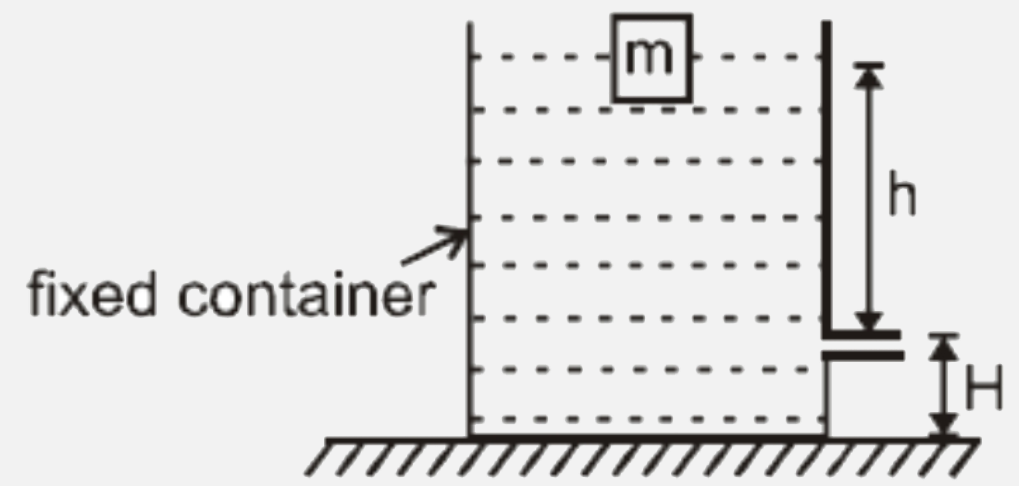
View SolutionA container filled with liquid up to height h is placed on a smooth horizontal surface. The container is having a small hole at the bottom. As the liquid comes out from the hole, the container moves in a backward direction with acceleration a and finally, when all the liquid is drained out, it acquires a velocity v. Neglect mass of the container. In this case
 View Solution
View SolutionA liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
View SolutionA tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :
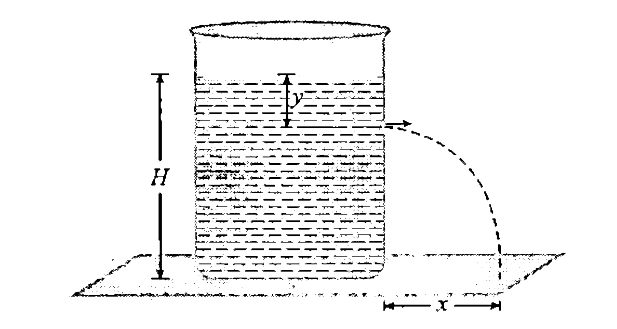 View Solution
View SolutionIn the figure shown, a light container is kept on a horizontal rough surface of coefficient of friction μ=ShV. A very small hole of area S is made at depth 'h'. Water of volume 'V' is filled in the container. The friction is not sufficient to keep the container at rest. The acceleration of the container initially is
 View Solution
View Solution

