Two vertical walls are separated by a distance of 2 metres. Wall 'A' is smooth while wall B is rough with a coefficient of friction $μ = 0.5$ . A uniform rod is propped between them. The length of the longest rod thhat can be probed between te walls is equal to

A

2 metres

B

$2 \sqrt{2}$ metres

C

$\sqrt{5}$ metres

D

$\frac{\sqrt{17}}{2}$ metres

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

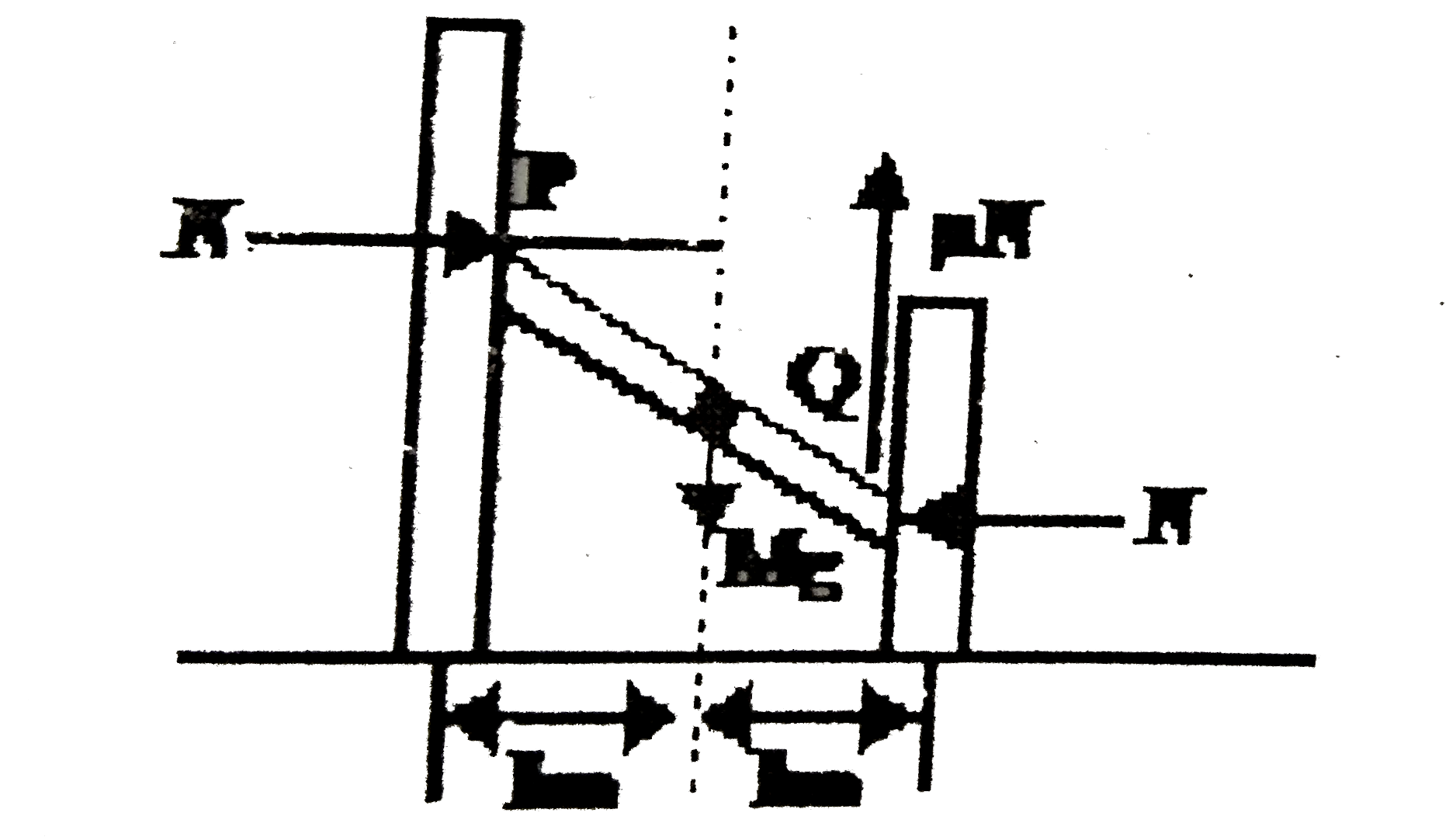
Drawing F.B.D. of rod PQ
$\sum F x = 0$
$\sum F y = 0 \Rightarrow μ N = m g$ …(1)
$\sum τ$ about centre of mass=0
$[N \times \frac{l}{2} sin θ] [2] = μ N \times \frac{l}{2} cos θ \Rightarrow tan θ = \frac{μ}{2}$
Hence $sec θ = (\sqrt{μ^{2} + 4}) / 2$
thus, $(\frac{l / 2}{1}) = \frac{\sqrt{μ^{2} + 4}}{2} \Rightarrow l = \sqrt{μ^{2} + 4}$
$\Rightarrow l = \sqrt{0.25 + 4} = \frac{\sqrt{17}}{2}$ metres.

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two vertical walls are separated by a distance of $2$ meters, Wall 'A' is smooth while wall $B$ is rough with a coefficient of friction $μ = 0.5$ A uniform rod is probed between them. The length of the longest rod that can be probed between the walls is equal to

A $2 m$
B $2 \sqrt{2} m$
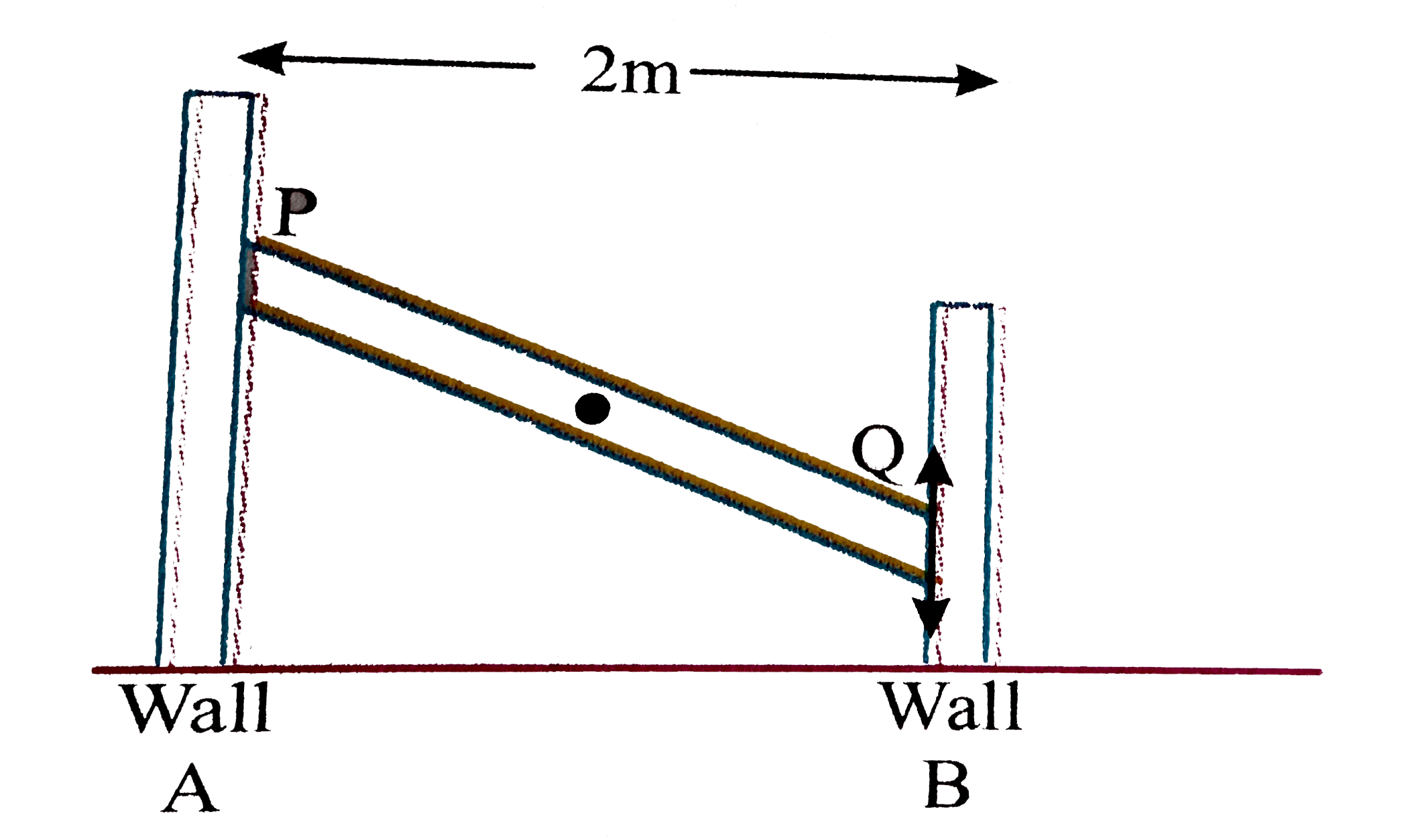C $\sqrt{2} m$
D $\frac{\sqrt{17}}{2} m$
Question 2 - Select One
A uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction $μ$ and its upper end against a smooth vertical wall. If $θ$ is the inclination of the ladder with the wall, then $θ$ is equal to
A ${tan}^{- 1} μ$
B ${cot}^{- 1} μ$
C ${cot}^{- 1} (2 μ)$
D ${tan}^{- 1} (2 μ)$
Question 3 - Select One
A uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction $μ$ and its upper end against a smooth vertical wall. If $θ$ is the inclination of the ladder with the wall, then $θ$ is equal to
A ${tan}^{- 1} μ$
B ${cot}^{- 1} μ$
C ${cot}^{- 1} (2 μ)$
D ${tan}^{- 1} (2 μ)$

FIITJEE-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile