A uniform disc of mass m and diameter 2R moves forward towards another uniform disc of mass 2m & diameter 2R on a frictionless surface as shown in figure

When the first disc contacts the second, they stick to each other and move as a single object.
the velocity of combined disc after the collision is V03
the angular velocity of combined disc after the collision is ω23
If ω0=83V0R, the combined disc will not rotate
If combined disc does not rotate, the energy loss is 199MV20
The correct Answer is:A, C, D
Momentum conservation
MV0=2MV
V=V03
Angular momentum conservation about centre of mass
12MR2.ω0−43MV0R=[MR22+M(43R)2+12(2M)R2+2M(23R2)]ω
ω=325ω0−825V0R
For ω=0
ω0=8V03R
The energy loss,
△E=Ei−Ef
=12MV20+12(MR22).ω2−12(3M)V2=199MV20
Topper's Solved these Questions
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-II)
Explore 20 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:COMPREHENSIONS ( Comprehension-II)
Explore 5 Videos
Similar Questions
Knowledge Check
A uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),
 Aits linear acceleration is g upwardBits linear acceleration is g downwardCits angular acceleration is 2gR .Dits rate of change of angular momentum is MgR .
Aits linear acceleration is g upwardBits linear acceleration is g downwardCits angular acceleration is 2gR .Dits rate of change of angular momentum is MgR .A disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at tihe instant shows is
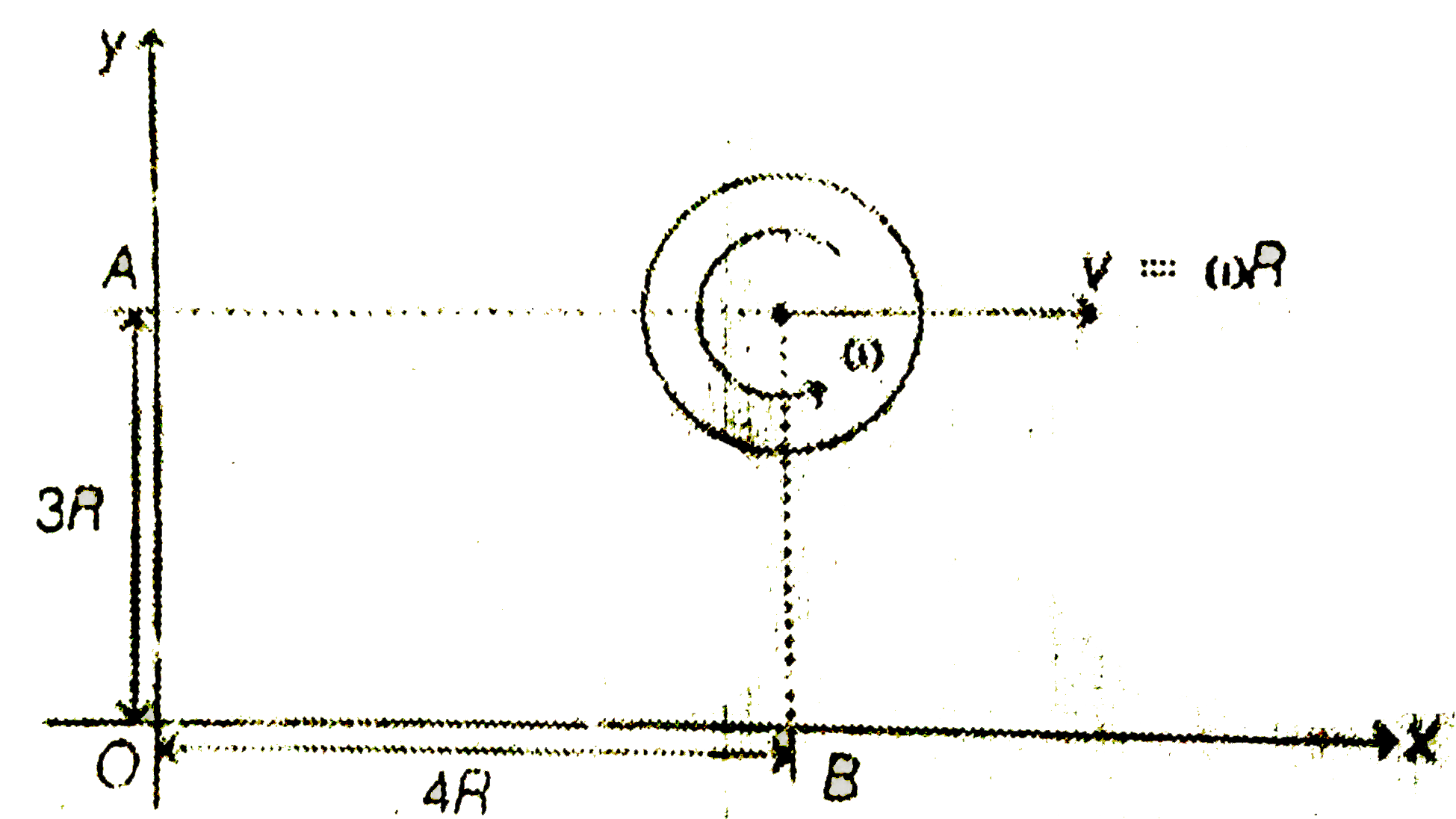 A52mR2ω about OB72mR2ω about OC12mR2ω about AD4mR2ω about A
A52mR2ω about OB72mR2ω about OC12mR2ω about AD4mR2ω about AA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is
 A−52mR2ωˆkB73mR2ωˆkC−92mR2ωˆkD52mR2ωˆk
A−52mR2ωˆkB73mR2ωˆkC−92mR2ωˆkD52mR2ωˆk
A disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at the instant shown is –
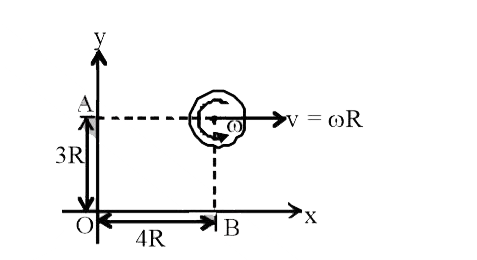
View SolutionThe distance of center of mass from the center of a uniform disc of radius R. if a circular plate is removed from the disc as shown in figure will be (C is centre of complete disc)
View SolutionA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is

View SolutionA system of uniform rod of mass m and length 2R and a uniform disc of m and radius R are as shown in the figure. The moment of inertia of the system about the axis OO′ (perpendicular to plane of disc) will be
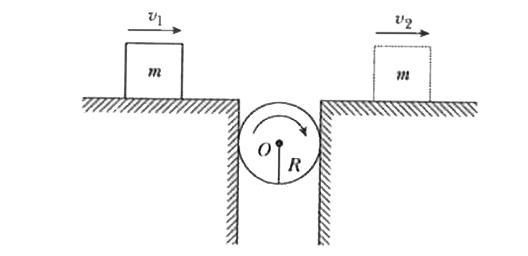
View SolutionA uniform disc of mass M and radius R is initially at rest. Its axis is fixed through O. A block of mass m is moving with speed v1 on a frictionless surface passes over the disc to the dotted position. On coming in contact with the disc, it slips on it. The slipping ceases before the block loses contact with the disc, due to the high friction. Now, the velocity of mass m is
View Solution
