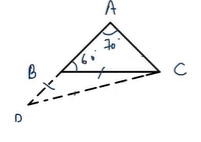
In ABC, side AB is produced to D so that BD=b⋅ If ∠B=600 and ∠A=700, prove that : (i)AD>CD (ii)AD>AC
Given that in △ABC, side AB is produced to D So that BD=BC and ∠B=600 and ∠A=700,
We have to prove that
(i) AD>CD
(ii)AD>AC
First join C and D
Now, in △ABC
Sum of angles in a triangle=1800
∠A∠B+∠C=1800
∠C=1800−700−600
1800−1300
∠C=500
∠ACB=500.........(i)
And also in △BDC,
∠DBC=1800−∠ABC............(ABC is a staight angle)
1800−600
1200
And also BD=BC.......(given)
∠BCD=∠BDC
Angle oopposite to equal sides are equal
Now,
Sum of angle in a triangle =180
∠DBC+an≥BCD+∠BDC=1800
1200+∠BCD+∠BCD=1800
2∠BCD=1800−1200
∠BCD=602=300
∠BCD=∠BDC=300............(ii)
Now, consider △ADC
∠BAC=∠DAC=700........(given)
∠BDC=∠ADC=300......(from (i) and (ii))
∠ACD=∠ACB+∠BCD
500+300......from equation (i) and (ii)
800
Now ,∠ADC<∠DAC<∠ACD
AC<DC<AD
AD>CD and AD>AC
Hence proved
Topper's Solved these Questions
Similar Questions
In ABC, side AB is produced to D so that BD=b⋅ If ∠B=600 and ∠A=700, prove that : (i)AD>CD (ii)AD>AC
View SolutionIn ABC, side AB is produced to D so that BD=BC. If ∠B=600 and ∠A=700, prove that: AD>CD (ii) AD>AC
 View Solution
View SolutionIn Fig. 4.124, E is a point on side CB produced of an isosceles triangle ABC with AB=AC . If AD⊥BC and EF⊥AC , prove that (i) ABDECF (ii) AB×EF=AD×EC . (FIGURE)
View SolutionIn Fig.81, side BC of ABC has been produced to D and CEBA. If ∠ABC=650, ∠BAC=550, find ∠ACE, ∠ECD and ∠ACD.
View SolutionIf a<b and c≤d, prove that a+c<b+d
View SolutionThe side BC of ABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC=300and ∠ACD=1150, then ∠ALC= 850 (b) 72120 (c) 1450 (d) none of these
View SolutionIn a ABC median AD is produced to X such that AD=DX . Prove that ABXC is a parallelogram.
View SolutionD is a point on the side BC of ABC. A line PDQ , though D , meets side AC in P and AB produced at Q . If ∠A=800, ∠ABC=600 and ∠PDC=150 find (i) ∠AQD (ii) ∠APD.
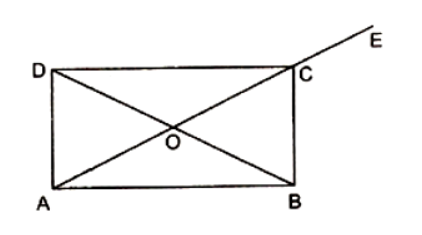
View SolutionIn Figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD=1460, find ∠AOB
 View Solution
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣DC, DC is produced to E such that CE=AB, prove that ar(ABD)=ar (BCE). Construction: Draw DM on BA produced and BN⊥DC
 View Solution
View Solution

