Angles opposite to two equal sides of a triangle
are equal.
GIVEN : ABC
in which AB=AC
TO PROVE : ∠C=∠B
CONSTRUCTION : Draw the bisector AD
of ∠A
which meets BC
in D
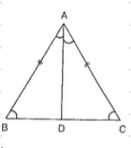
Step by step video solution for Angles opposite to two equal sides of a triangle are equal. GIVEN : A B C in which A B=A C TO PROVE : /_C=/_B CONSTRUCTION : Draw the bisector A D of /_A which meets B C in D by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If two sides of a triangle are unequal, the longer side has greater angle opposite to it. GIVEN : A ABC in which AC>AB. TO PROVE : ∠ABC>∠ACB
CONSTRUCTION : Mark a point D on AC such that AB=AD. Joint BD.
View SolutionShow that a median of a triangle divides it into two triangles of equal area. GIVEN : A ABC in which AD is the median. TO PROVE : ar(ABD)=ar(ADC) CONSTRUCTION : Draw AL⊥BC
View SolutionIf the bisector of the vertical angle of a triangle bisects the base of the triangle. then the triangle is isosceles. GIVEN : A ABC in which AD is the bisector of ∠A meeting BC in D such that BD=DC.
View SolutionShow that the difference of any two sides of a triangle is less than the third side. GIVEN : ABC TO PROVE : (i) AC−AB<BC BC−AC<AB (iii) BC−AB<AC CONSTRUCTION : Take a point D on AC such that AD=AB. Join BD.
View SolutionThe sum of any two sides of a triangle is greater than the third side. GIVE : A ABC
View SolutionProve that any two sides of a triangle are together greater than twice the median drawn to the third side. GIVEN : ABC in which AD is a median. PROVE : AB+AC>2AD CONSTRUCTION : Produce AD to E such that AD=DE. Join EC.
View SolutionProve that the area of an equilateral triangle is equal to √34a2, where a is the side of the triangle. GIVEN : An equilateral triangle ABC such that AB=BC=CA=a. TO PROVE : ar(ABC)=√34a2 CONSTRUCTION : Draw AD⊥BC.
View SolutionIn a right angled triangle, one acute angle is double the other. Prove that the hypotenuse is double the smallest side. GIVEN : A ABC in which ∠B=900 and ∠ACB=2∠CAB . to prove : AC=2BC CONSTRUCTION : Produce CB to D such that BD=CB. Join AD.
View SolutionFill the blanks in the following so that each of the following statements is true.
(i) Sides opposite to equal angles of a triangle are ......
(ii) Angle opposite to equal sides of a triangle are .....
(iii) In an equilateral triangle all angles are .....
(iv) In a ΔABC if ∠A = ∠C , then AB = ......
(v) If altitudes CE and BF of a triangle ABC are equal, then AB = ....
(vi) In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
(vii) In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC ≅ Δ ……
View SolutionShow that the sum of the three altitudes of a triangle is less than the sum of three sides of the triangle. GIVEN : A ABC in which AD⊥BC,BE⊥AC and CF⊥AB. PROVE : AD+BE+CF<AB+BC+AC
View Solution
