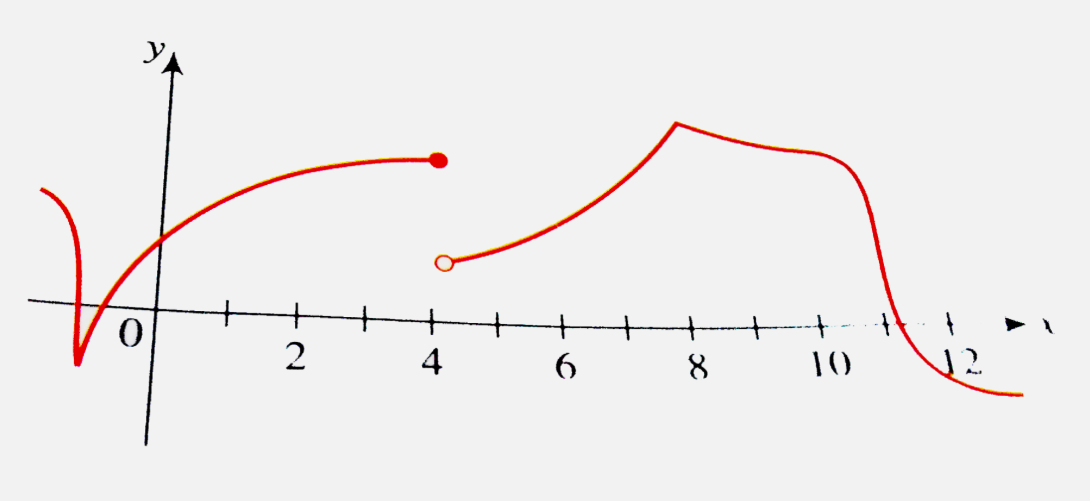
The graph of f is shown. State, with reason, the numbers at which f is not differentiable.
Text Solution
At x =- 4, f is discontinuous, hence non-differentiable.
At x =- 1, f is continuous but has corner, hence non-differentiable.
At x = 2, f has vertical asymptote, hence non-differentiable.
At x = 5, f has vertical tangent, hence non-differentiable.
|
Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBOOK - CENGAGECHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercise
18 Videos
- FUNCTIONSBOOK - CENGAGECHAPTER - FUNCTIONSEXERCISE - Question Bank
30 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
Similar Questions
Knowledge Check
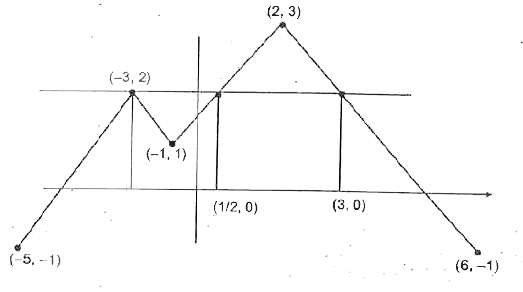
The graph of y = f(x} is shown, then the number of solutions of f(f(x}} = 2 will be
 A1B2C3D4
A1B2C3D4The graph of y=f(x) is shown to the right. If f(−1)=v, then which one of the following could be the value of f(v) ?
 A0B1C2D2.5
A0B1C2D2.5
If f(x)=||x|-1| ,then the number of points where f(x) is not differentiable is
View SolutionThe graph of f is given.
State the equations of all the asymptotes.

View SolutionThe graph of y = f(x) is shown, find the number of solution of f(f(x)) = 2.

View SolutionUsing graph find the number of points where g(x) is non differentiable. f(x)=x−3;x<0,x2−3x+2;x>0orx=0g(x)=f(|x|)+|f(x)|
View SolutionThe graph of the function y=f(x) is shown.

Find the number of solutions to the equation ||f(x)|−1|=12.
View SolutionThe graph of the function y=f(x) is shown.

Find the number of solutions to the equation ||f(x)|−1|=12.
View Solution