An equimolar mixture of a mono atomic and diatomic gas is subjected to continuous expernsions such that dQ=13dU+12dW. The equation of the process in terms of the variable P & V will be
PV5/4=constant
PV11/8=constant
PV8/3=constant
PV9/4= constant
dQ=13du+12dw
From 1st law of thermodynamics,
dQ=du+dw
dQ=ncdt.C=®γ−1+R1−n for PVn process.
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
Knowledge Check
Ideal mono-atomic gas is taken through process such that dQ = 3dU. The molar heat capacity for process is:
A3RB4.5RC4RD2RAn amount Q of heat is added to a mono atomic ideal gas in a process in which the gas performs a work Q/2 on its surrounding. Find equation of the process.
ATV1/3= constantBTV−1/4= constantCTV1/4= constantDTV−1/3= constantA mixture of n1 moles of monoatomic gas and n2 moles of diatomic gas has γ=1.5
An1=n2B2n1=n2Cn1=2n2Dn1=3n2
1mol of a mono-atomic gas is subjected to following cyclic process:
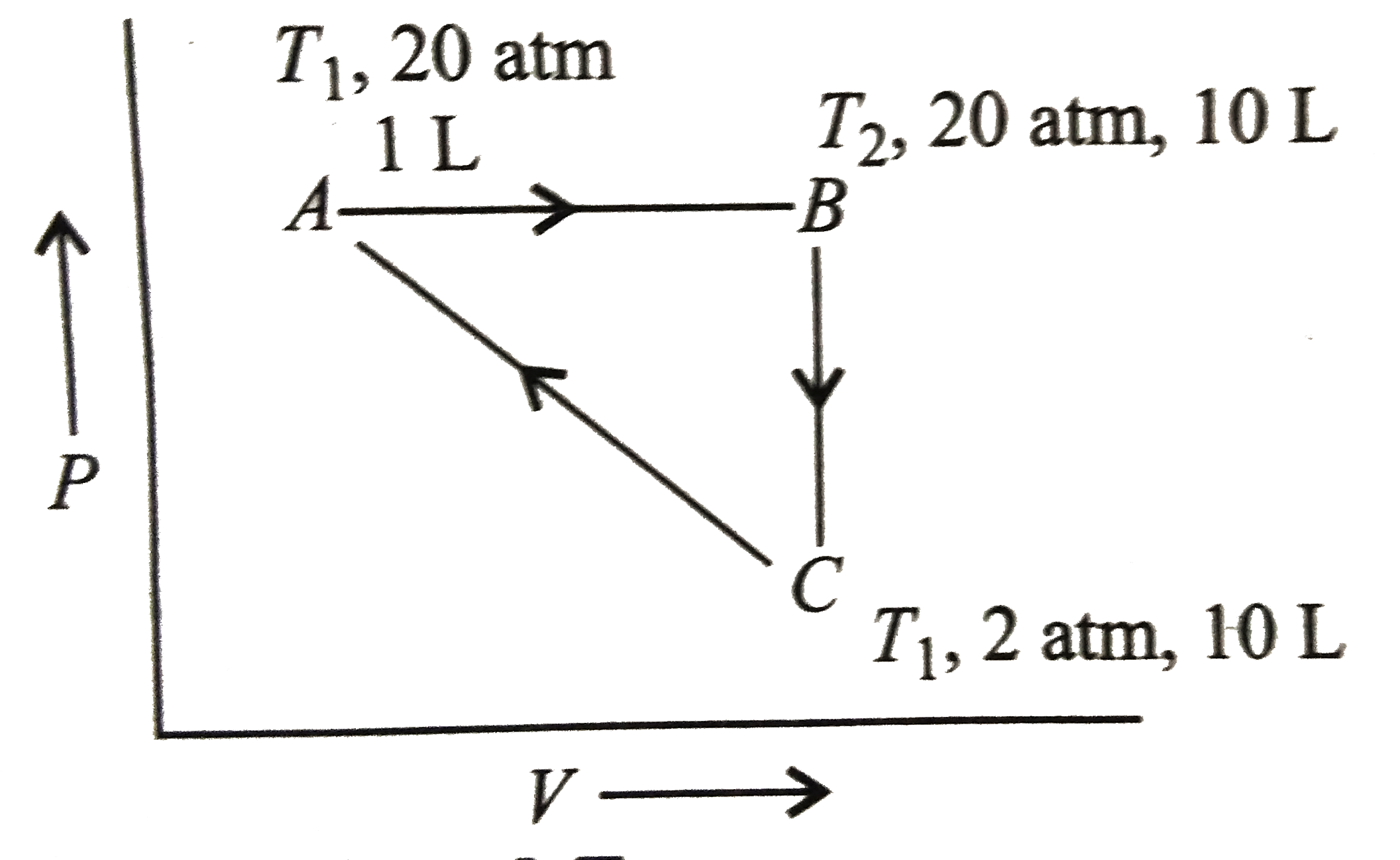
a. Calculate T1 and T2.
b. Calculate ΔU,q, and W in calories in each step of cyclic process.
View SolutionTwo ideal monoatomic and diatomic gases are mixed with one another to form an ideal gas mixture. The equation of the adiabatic process of the mixture is PVγ= constant, where γ=117 If n1 and n2 are the number of moles of the monoatomic and diatomic gases in the mixture respectively, find the ratio n1n2
View SolutionTwo ideal monoatomic and diatomic gases are mixed with one another to form an ideal gas mixture. The equation of the adiabatic process of the mixture is PVγ= constant, where γ=117 If n1 and n2 are the number of moles of the monoatomic and diatomic gases in the mixture respectively, find the ratio n1n2
View SolutionFor an ideal gas the molar heat capacity varies as C=CV+3aT2. Find the equation of the process in the variables (T,V) where a is a constant.
View SolutionThe molar specific heat of a gas is defined as C=DqndT Where dQ=heat absorbed
n = mole number dT = change in temperature
The equation of the above process in the variables T,V is
View Solution
