A disc -shaped pulley has mass M = 4 kg and radius R = 0.5 m . It rotates freely on a horizontal axis , as in fig . A block of mass m = 2 kg hangs by a string that is tightly wrapped around the pulley .
(a) What is the angular velocity of the pulley 3s after the block released ?
(b) Find the speed of the after it has fallen 1.6 m .
Assume the system starts at rest .

Since the string is tangetial to the pulley , the torque on it due to the tension is τ=TR . The two forms of Newton.s second law for the block and the pulley yield
Block (F=ma) mg−T=ma
Putting (τ=Iα)TR=(12MR2)α
Applying Newton.s second Law τ=Iα
For the disc , I=MR22
∴TR(MR2α)orT=MRα2....(i)
Applying Newton.s second Law on the block
Fnet=ma
∴mg−Tma ......(ii)
Since the block and the rin of pulley have the same speed ( the string does not slip ) , we have v=ωR . Thus , from equation (i) we find
T=12Ma ....(iii)
Adding (ii)and (iii) leads to a=mgmM2.....(iv)
Puttng m = 2 kg , M = 4 kg , R = 0.5 m ,
e get , a=5m/s2
(a) To find ω after 3s , we use equation
ω+ω0+αt=0(aR)t=30rad/s
(b) To find the speed of the block we use
v2=v20+2ay=0+2=0+2(5m/s2)(1.6m)
Thus v = 4m/s
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 1
9 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 4
11 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
A disc shaped pulley of mass 'm'=4kg and radius R=0.5m can rotate freely about its center. A block of mass M=2kg hangs from the pulley through is massless string that is tightly wrapped around the pulley. When the system is released, there is no slipping between pulley and string.
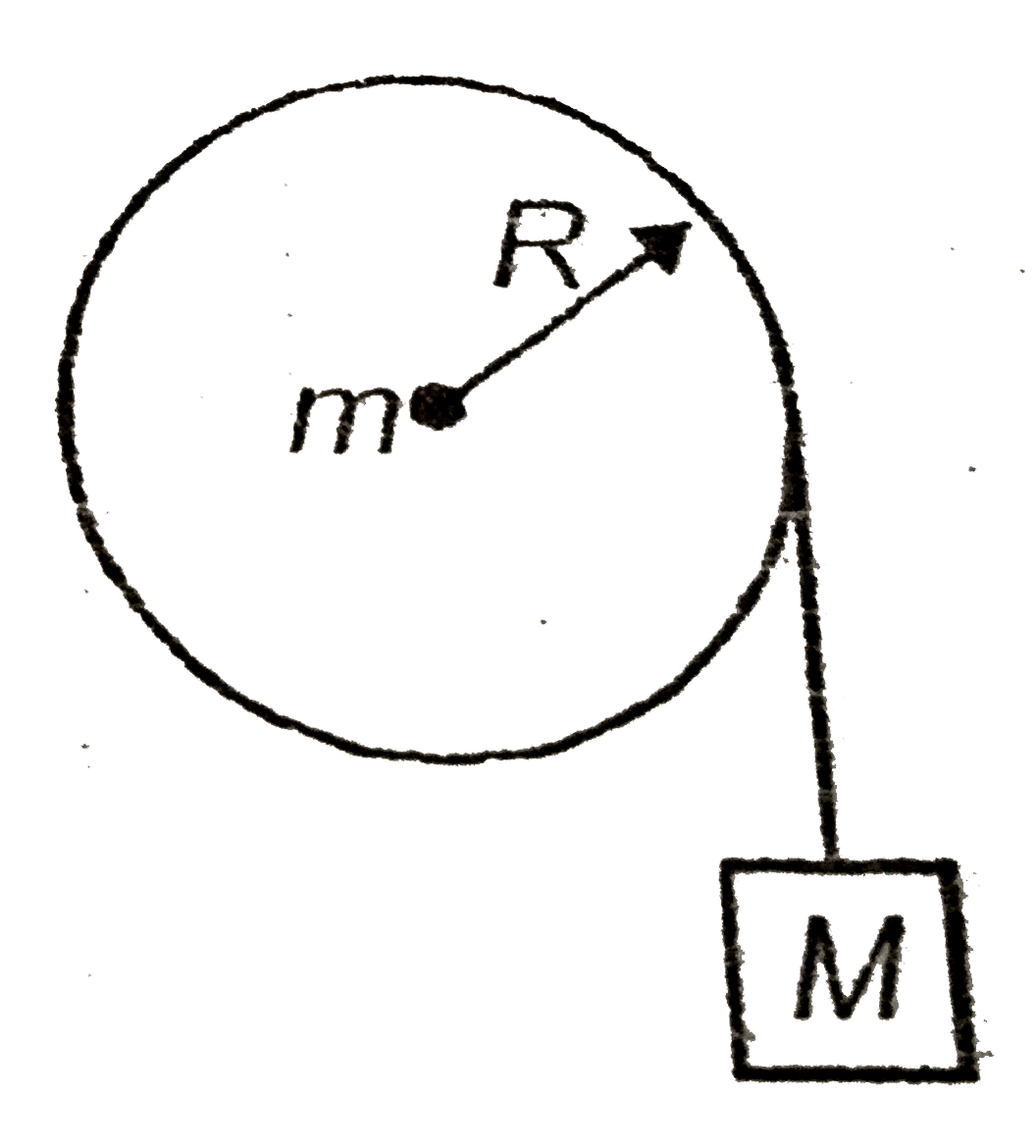
(a) Calculate the angular accelerating of the pulley
(b) Calculate the tension in the string
View SolutionA disc shaped pulley of mass 'm'=4kg and radius R=0.5m can rotate freely about its center. A block of mass M=2kg hangs from the pulley through is massless string that is tightly wrapped around the pulley. When the system is released, there is no slipping between pulley and string.

(a) Calculate the angular accelerating of the pulley
(b) Calculate the tension in the string
View Solution
Knowledge Check
The figure shows a uniform disc, with mass M = 2.4 kg and radius R= 20 cm, mounted on a fixed horizontal axle. A block of mass m = 1.2 kg hangs from a massless cord that is wrapped around the rim of the disc. The tension in the cord is
 A12 NB20 NC24 NDnone of these
A12 NB20 NC24 NDnone of theseA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
A2MM+2mgB2mM+2mgCM+2m2MgD2M+m2MgA disc of mass 2 kg and radius 0.2 m is rotating with angular velocity 30 rad/s What is angular velocity, if a mass of 0.25 kg put on periphery of the disc ?
A24rad/sB36rad/sC15rad/sD26rad/s
A uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
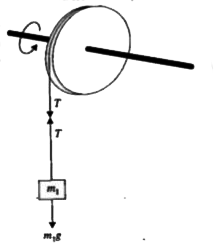
View SolutionA wheel of mass 1.4 kg and radius 0.4 m is mounted on a frictionless, horizontal axle as shown in Fig. 7.2.50. Alight string wrapped around the rim supports a mass of 2 kg. What is the angular acceleration of the wheel and the tangential acceleration of a point on the rim ? Also find the tension in the string.
View SolutionA metallic pulley is in the shape of a disc of radius a. It can rotate freely about a horizontal axis passing through its centre. The moment of inertia of the pulley about this axis is I. A light string is tightly wrapped around the pulley with its one end connected to a block of mass M. The centre of the pulley and its circumference are connected to a resistance R as shown. The contact of resistance at the circumference does not cause any friction. A uniform magnetic field B is switched on which is parallel to the axis of rotation of the pulley (see Figure). The mass M is allowed to fall. Assume that resistivity of the material of the pulley is negligible.
(a) Find the acceleration of the block of mass M at the instant its velocity becomes v0.
(b) Assuming that the block can fall through a large distance, calculate the terminal speed (vT) that it will acquire.
(c) Find the rate of change of kinetic energy of the pulley at the instant speed of the falling block is vT2.

View SolutionA disc of mass 2 kg and radius 0.2 m is rotating with angular velocity 30 rad/s What is angular velocity, if a mass of 0.25 kg put on periphery of the disc ?
View SolutionA disc of mass 2 kg and radius 0.2 m is rotating with angular velocity 30rad s−1. What is angular velocity, if a mass of 0.25 kg is put on periphery of the disc ?
View Solution
