Find the area enclosed by the figure described by the equation x4+1=2x2+y2.
Video Solution
Text Solution
The correct Answer is:83 sq. units
x4+1=2x2+y2
∴ x4−2x2+1=y2
∴ (x2−1)2=y2
∴ y=±(x2−1), which are two parabolas.
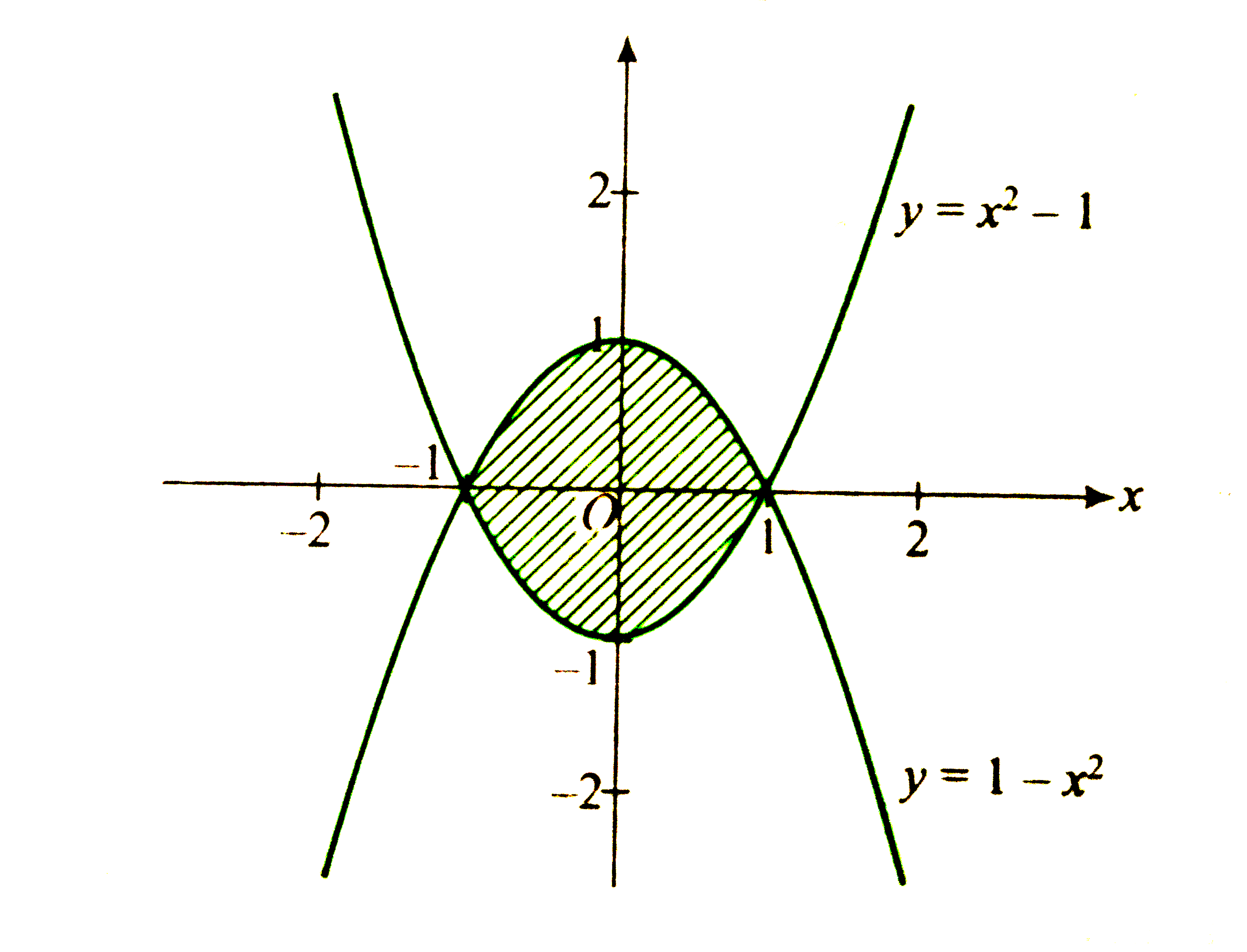
Required area A=41∫0(1−x2)dx
=4[x−x33]10=83 sq. units.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.37videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Single)40videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.19videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank29videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank20videos
AREA UNDER CURVES
Similar Questions
Find the area enclosed by the circle x2+y2=25
View SolutionFind area enclosed by |x|+|y|=1.
View SolutionFind the area enclosed by the circle x2+y2=9.
View SolutionFind the area enclosed by the curves y=4x2 and y2=2x.
View SolutionFind the area enclosed by the curves
max(2|x|,2|y|)=1View SolutionFind the area enclosed by the curve x2=4y and the abcissa y=1
View SolutionFind the area enclosed by the circle x2+y2=a2.
View SolutionFind the area of the region enclosed by the curve y=x4–2x2andy=2x2.
View Solutionwhat is the area enclosed by the equation x2+y2=2
View SolutionFind the area enclosed by the curves x2=y,y=x+2,andx−aξs.
View Solution

