Question

Find the area of the region bounded by the curves $y=x^2+2;y=x;x=0$ and $x=3$

Answer

`(21)/(2)` sq. units

Explanation

`y=x^(2)+2` is parabola having vertex at (0,2) and having concavity upward.

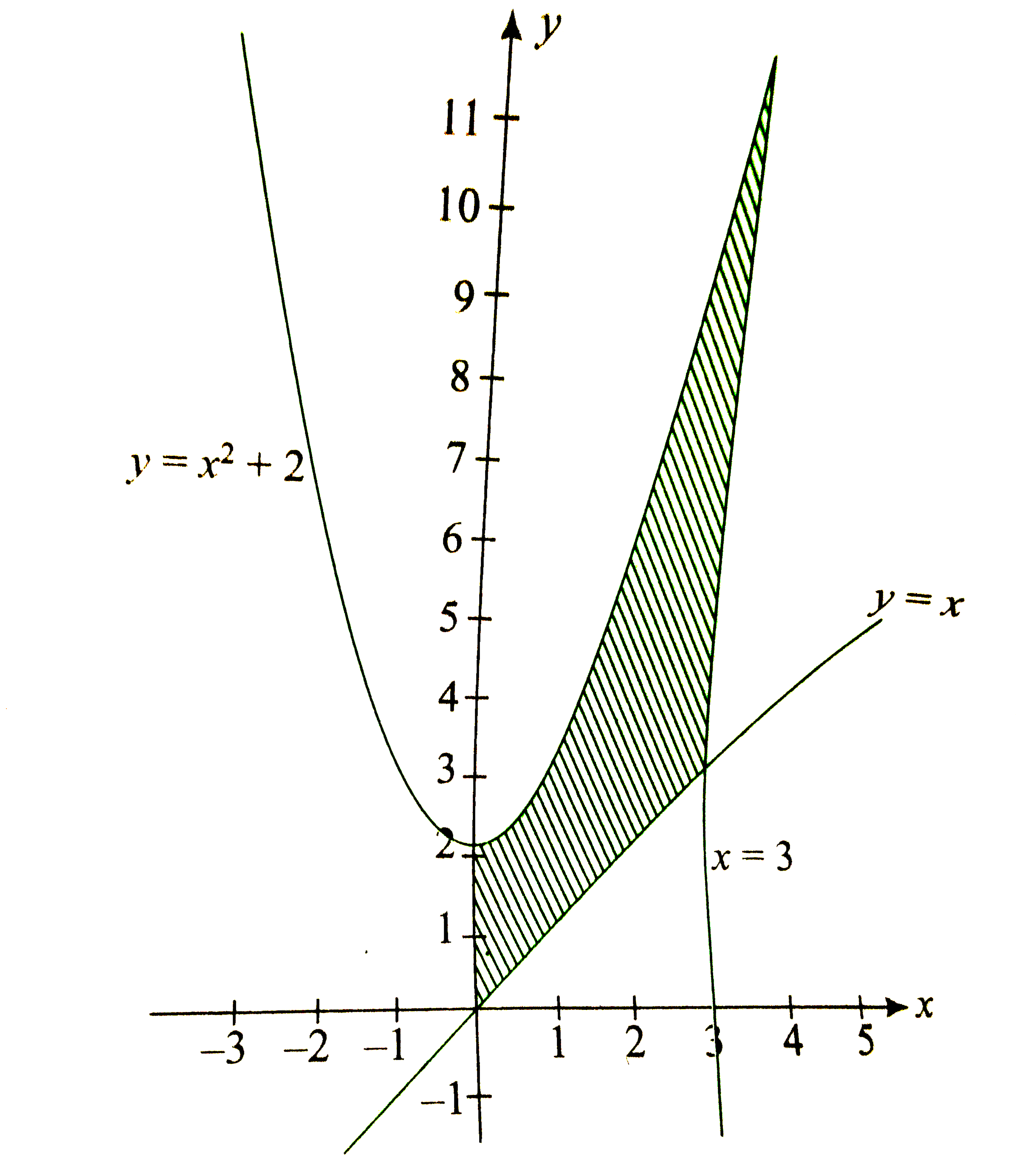
`"Then, required area "=int_(0)^(3)((x^(2)+2)-x)dx=[(x^(3))/(3)+2x]_(0)^(3)-[(x^(2))/(2)]_(0)^(3)`
`=[9+6]-[(9)/(2)]=(21)/(2)` sq. units.