Question

Sketch the region bounded by the curves $y=\sqrt{5-x^2}$
and $y=|x-1|$
and find its area.

Answer

`(5pi-2)/(4)` sq. units

Explanation

The given curves are
`y=sqrt(5-x^(2))" (1)"`
`y=|x-1|" (2)"`
We can clearly see that on squaring the both sides of (1), equation (2) represents a circle.
But as y is + ve square root, (1) represents the upper-half of the circle with centre (0,0) and radius `sqrt(5)`.
Equation (2) represents the curve
`y={(-x+ if x lt 1),(x-1 if x ge 1):}`

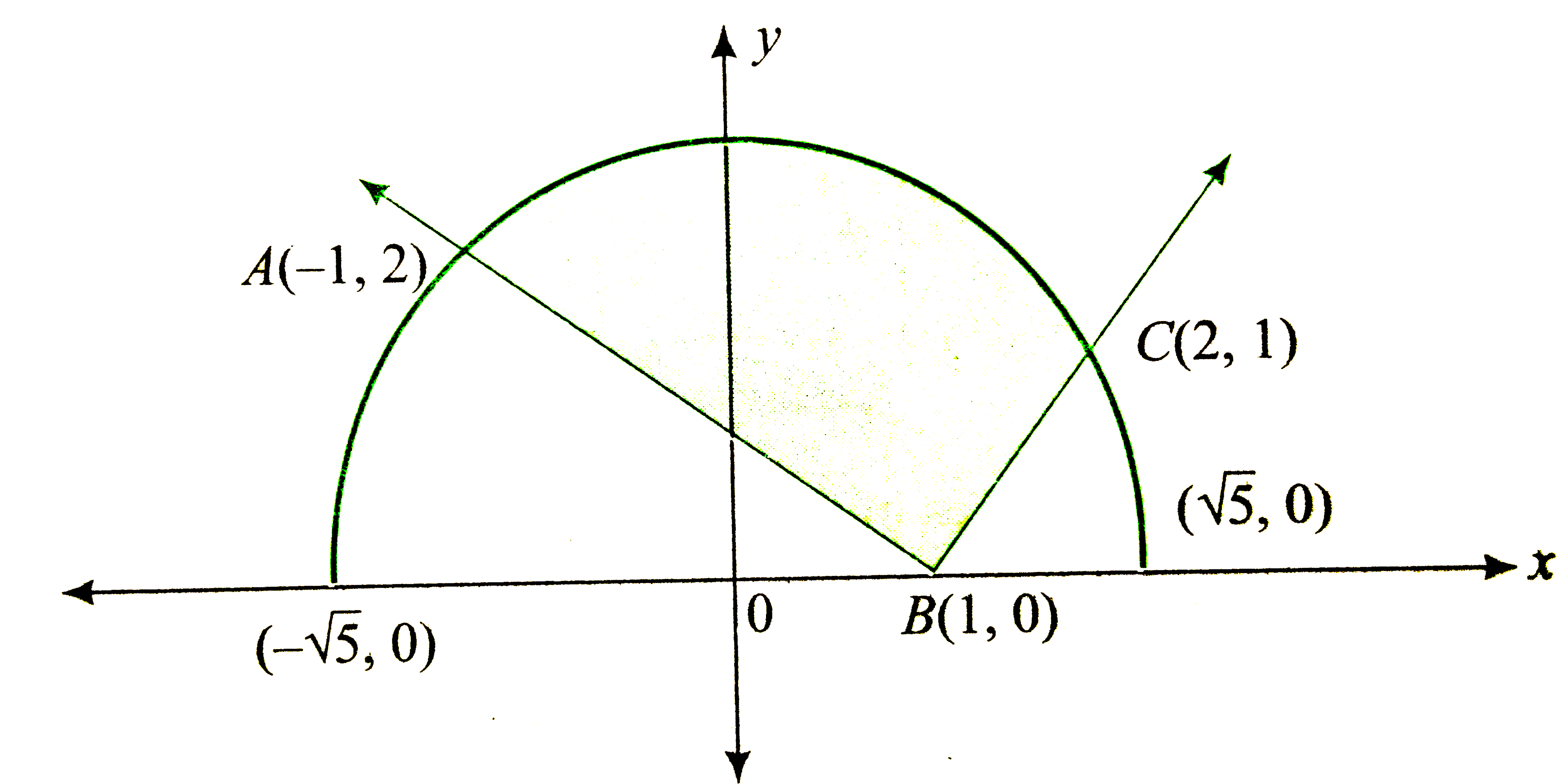
Graph of these curves are as shown in the figure with point of intersection of `y=sqrt(5-x^(2)) and y=-x +1 as A(-1,2)`
`"and of "y=sqrt(5-x^(2)) and y=x-1 as C(2,1)`
`therefore" Required area = Shaded area"`
`=int_(-1)^(2)sqrt(5-x^(2))dx-int_(-1)^(2)|x-1| dx`
`=[(x)/(2)sqrt(5-x^(2))+(5)/(2)sin^(-1)((x)/(sqrt(5)))]_(-1)^(2)-int_(-1)^(1)-(x-1)dx-int_(1)^(2)(x-1)dx`
`=((2)/(5)sqrt(5-4)+(5)/(2) sin^(-1)""(2)/(sqrt(5)))-((-1)/(2)sqrt(5-1)+(5)/(2)sin^(-1)((-1)/(sqrt(5))))-((-x^(2))/(2)+x)_(-1)^(1)-((x^(2))/(2)-x)_(1)^(2)`
`=1+(5)/(2)sin^(-1)""(2)/(sqrt(5))+1+(5)/(2)sin^(-1)((1)/(sqrt(5)))`
`-[((-1)/(2)+1)-((-1)/(2)-1)]-[(2-2)-((1)/(2)-1)]`
`=2+(5)/(2)[sin^(-1)""(2)/(sqrt(5))+sin^(-1)""(1)/(sqrt(5))]-2-(1)/(2)`
`=(5)/(2)[sin^(-1)""(2)/(sqrt(5))+cos^(-1)""(2)/(sqrt(5))]-(1)/(2)=(5)/(2)((pi)/(2))-(1)/(2)`
`(5pi-2)/(4)` sq. units