Find the area bounded by y=−(log)ex,y=−(log)ex,y=(log)e(−x),andy=−(log)e(−x).
Video Solution
Text Solution
The correct Answer is:4 sq. units
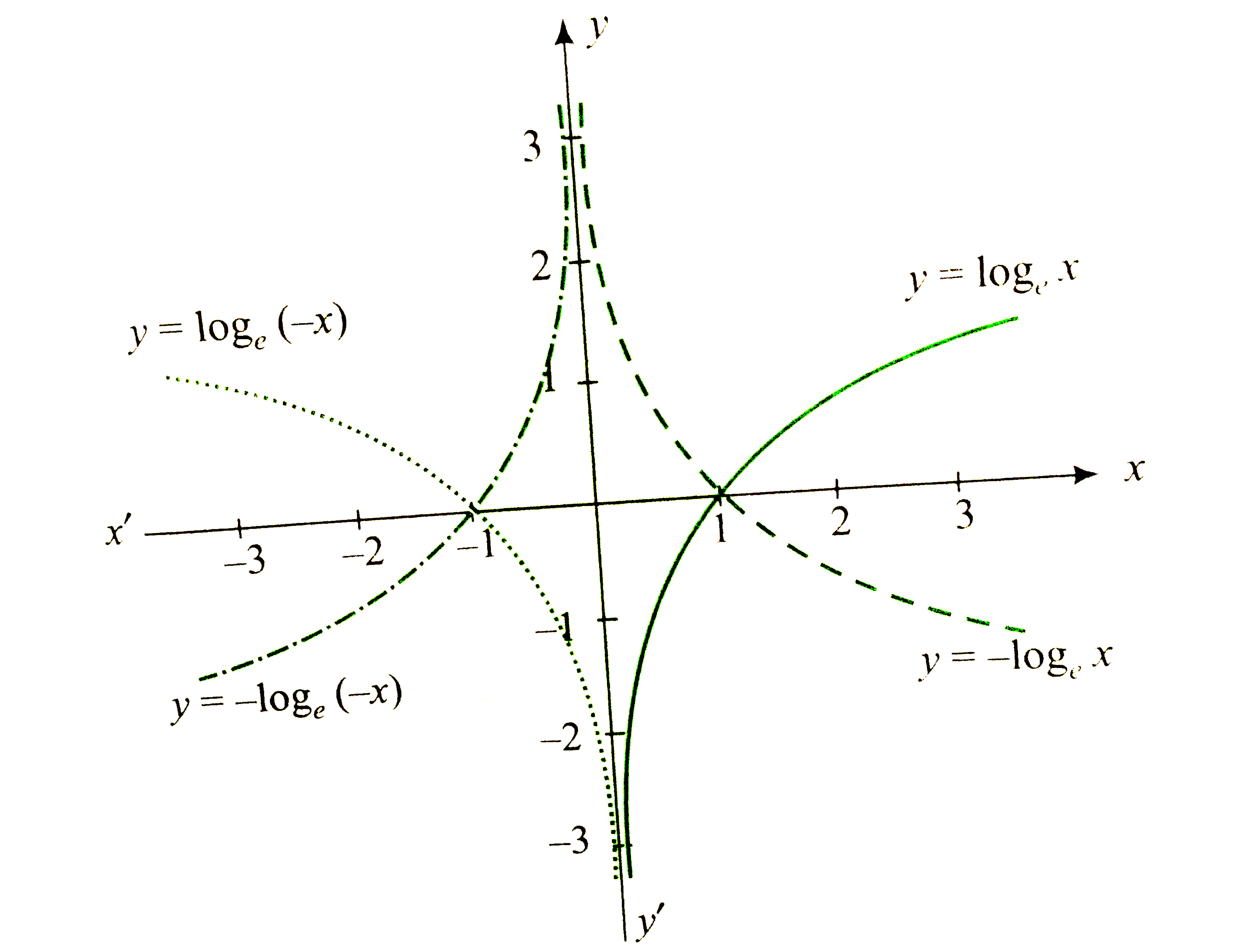
From the figure, required area = area of shaded region
=1+1+1+1=4 sq. units.
|
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.3
7 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Single)
40 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
If y=elogex, then dydx=
A0BxCeD1If y=logex(logx),thendydx
A2xlogxB−2xlogxC12xlogxD−12xlogx
Find the area bounded by a . y=(log)e|x|andy=0 b y=∣∣(log)3∣∣x∣∣andy=0
View SolutionFind the area bounded by
(i) y=loge|x|andy=0
(ii) y=|loge|x||andy=0
View SolutionFind the range of f(x)=(log)ex−((log)ex)2∣∣(log)ex∣∣
View SolutionCompute the area of the region bounded by the curves y=ex(log)exandy=logxex
View SolutionFind the area bounded by the curve y=logx, x-axis and the ordinates x=1&x=e.
View SolutionFind dydx of y=x(log)ex
View Solution
