In what ratio does the x-axis divide the area of the region bounded by the parabolas $y = 4 x - x^{2} a n d y = x^{2} - x ?$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $121 : 4$

Both are given curves are parabola
$y = 4 x - x^{2} (1)$
$and y = x^{2} - x (2)$
Solving (1) and (2), we get
$4 x - x^{2} = x^{2} - x$
$or x = 0, x = \frac{5}{2} .$
Thus, two curves intersect at $O (0, 0) and A (\frac{5}{2}, \frac{15}{4})$

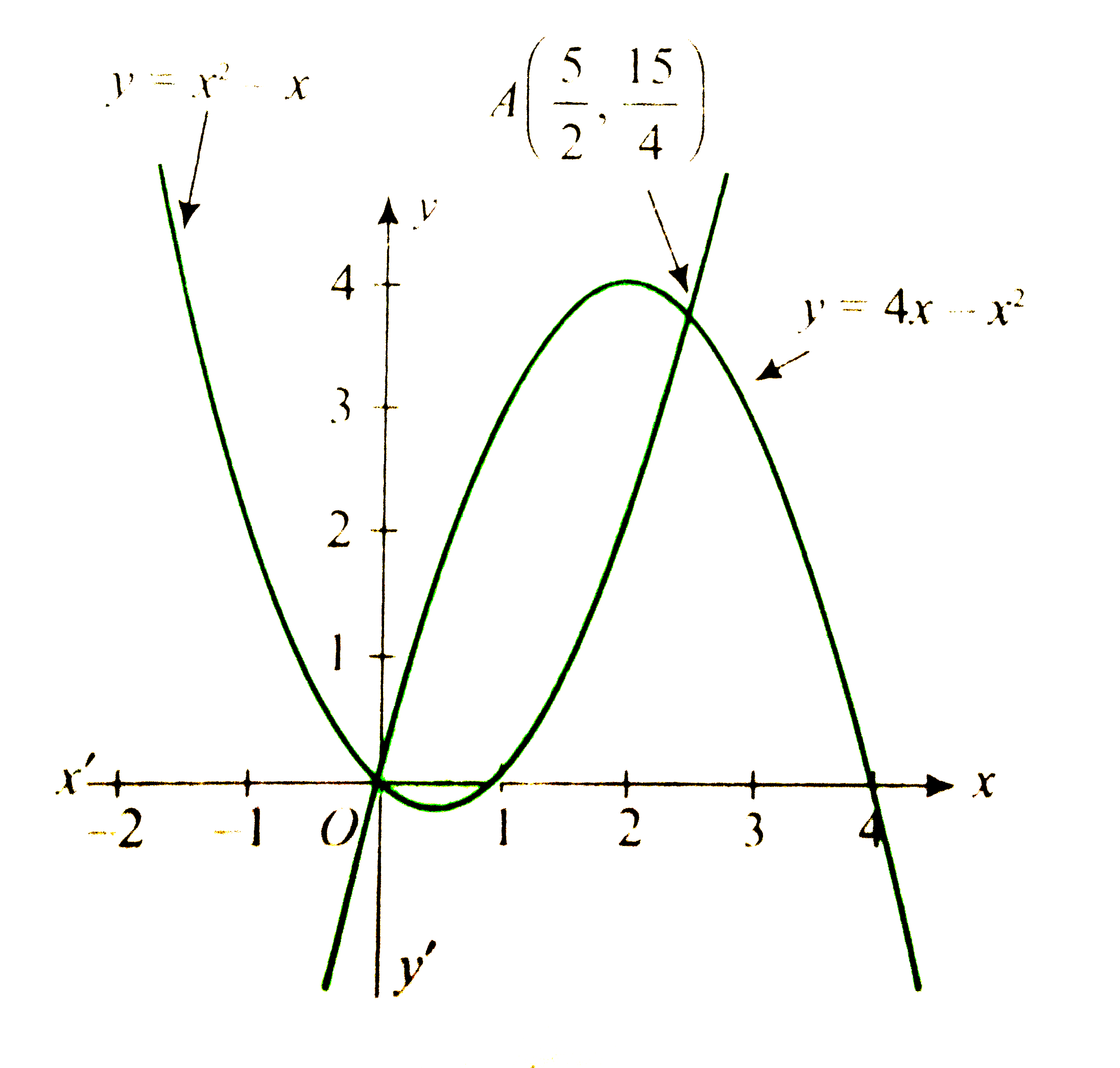
Here the area below x-axis,
$A_{1} = \int_{0}^{1} (x - x^{2}) d x$
$= {(\frac{x^{2}}{2} - \frac{x^{3}}{3})}_{0}^{1} = \frac{1}{2} - \frac{1}{3} = \frac{1}{6}$ sq. units
Area above x-axis,
$A_{2} = \int_{0}^{5 / 2} (4 x - x^{2}) d x - \int_{1}^{5 / 2} (x^{2} - x) d x$
$= {(2 x^{2} - \frac{x^{3}}{3})}_{0}^{2} - {(\frac{x^{3}}{3} - \frac{x^{2}}{2})}_{1}^{5 / 2}$
$= (\frac{25}{2} - \frac{125}{4}) - [(\frac{125}{4} - \frac{25}{8}) - (\frac{1}{3} - \frac{1}{2})]$
$= \frac{25}{2} - \frac{125}{2} + \frac{25}{8} - \frac{1}{6}$
$= \frac{300 - 250 + 75 - 4}{4} = \frac{121}{24}$ sq. units.

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area of the region bounded by the parabola $y = x^{2}$ and the line y = 4x is
A $\frac{32}{3} s q . u n i t s$
B $\frac{16}{3} s q . u n i t s$
C $\frac{8}{3} s q . u n i t s$
D $\frac{4}{3} s q . u n i t s$
Question 2 - Select One
What is the area of the region bounded by the parabola $y^{2} = 6 (x - 1)$ and $y^{2} = 3 x$ ?
AA. $\frac{\sqrt{6}}{3}$
BB. $\frac{2 \sqrt{6}}{3}$
CC. $\frac{4 \sqrt{6}}{3}$
DD. $\frac{5 \sqrt{6}}{3}$
Question 3 - Select One
The area of the region bounded by the parabola $y = 4 x - x^{2}$ , the X-axis, x=0 and x=2 is
A $\frac{8}{3}$
B $\frac{16}{3}$
C $\frac{16 - \sqrt{2}}{3}$
D $\frac{8 + \sqrt{2}}{3}$

CENGAGE-AREA-Exercise 9.2

Home
Ask Doubt
Profile