ABC is an equilateral triangle with O as its centre. →F1,→F2 and →F3 represent three force acting along the sides AB, BC and AC respectively. If the total torque about O is zero the magnitude of →F3 is :

F1+F2
F1−F2
F1+F22
2(F1+F2)
The correct Answer is:A
F1x+F2x=F3ξmpliesF3=F1+F2
Topper's Solved these Questions
- SYSTEM OF PARTICLES & ROTATIONAL MOTION BOOK - DISHA PUBLICATIONCHAPTER - SYSTEM OF PARTICLES & ROTATIONAL MOTION EXERCISE - EXERCISE-2 : CONCEPT APPLICATOR
28 Videos
- SYSTEM OF PARTICLES & ROTATIONAL MOTION BOOK - DISHA PUBLICATIONCHAPTER - SYSTEM OF PARTICLES & ROTATIONAL MOTION EXERCISE - EXERCISE-2 : CONCEPT APPLICATOR
28 Videos
- SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - DISHA PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - EXERCISE -2: CONCEPT APPLICATOR
25 Videos
- THERMAL PROPERTIES OF MATTER BOOK - DISHA PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTER EXERCISE - Exercise-2 (Concept Applicator)
28 Videos
Similar Questions
ABC is an equilateral with O as its centre →F1,→F2 and →F3 represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero then the magnitude of →F3 is :
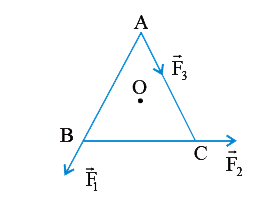
View SolutionABC is an equilateral triangle with O as its centre −→F1,−→F2 and −→F3 represent three forces acting along the sides AB, BC and AC respectively. If the torque about O is zero then the magnitude of −→F3 is

View Solution
Knowledge Check
O is the centre of an equilateral triangle ABC. F1,F2 and F3 are the three forces acting along the sides AB,BC and AC respectively. What should be the value of F3 so that the total torque about O is zero?
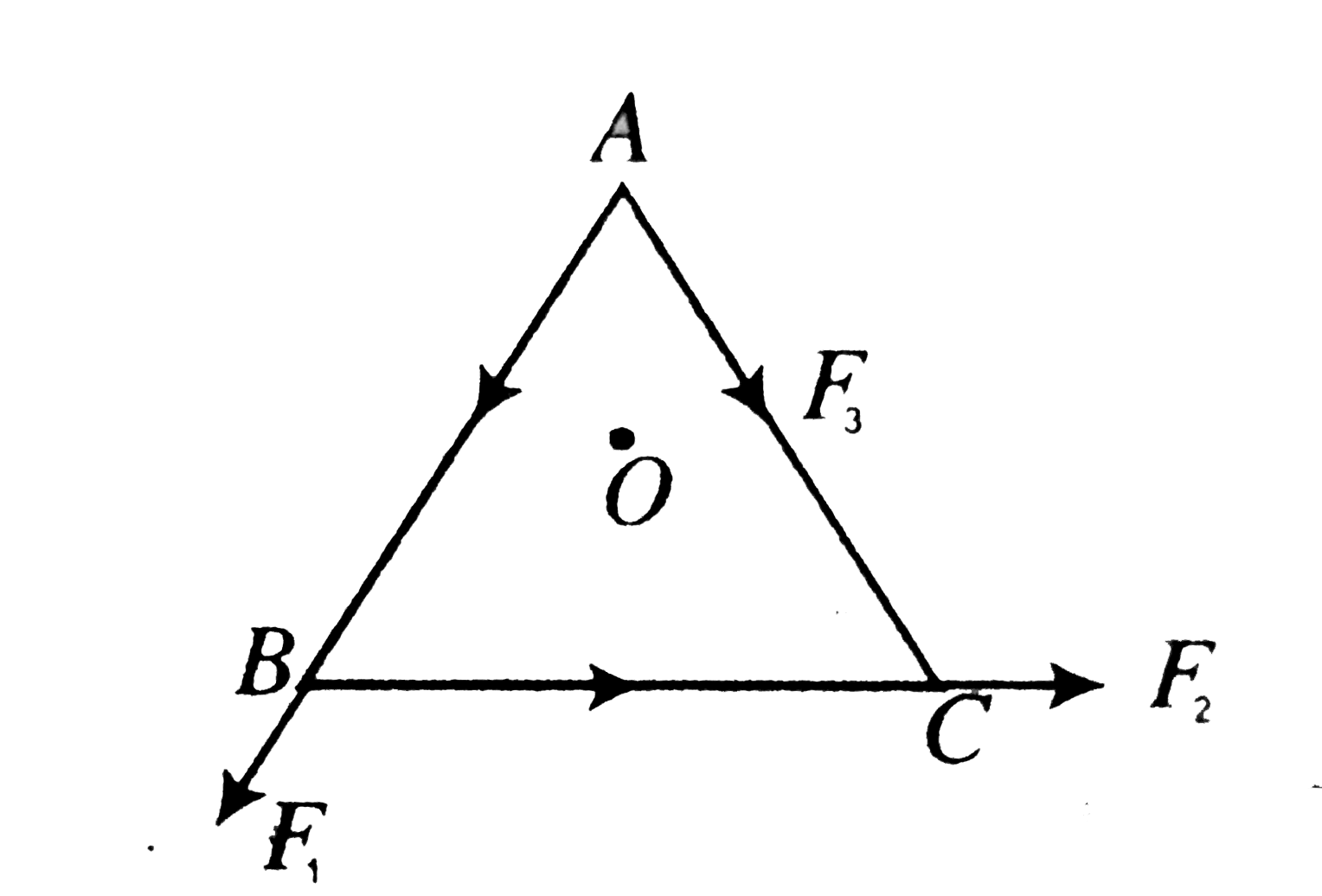 A2(F1+F2)BF1+F22CF1−F2DF1+F2
A2(F1+F2)BF1+F22CF1−F2DF1+F2O is the centre of an equilateral triangle ABC. F1,F2 and F3 are three forces acting along the sides AB, BC and AC as shown in the figure. What should be the magnitude of F3, so that the total torque about O is
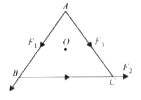 A(F1+F2)B2(F1+F2)C(F1+F2)/2D(F1−F2)
A(F1+F2)B2(F1+F2)C(F1+F2)/2D(F1−F2)A body is under the action of three forces →F1,→F2and→F3. In which case the body cannot undergo angular acceleration ?
A−→F1,−→F2and−→F3 are concurrentB−→F1+−→F2+−→F3=0C−→F1,−→F2 is parallel to −→F3 but the three forces are not concurrentD−→F1and−→F2 act at the same point but −→F3 acts at different point.
O is the centre of an equilateral triangle ABC. F1,F2 and F3 are the three forces acting along the sides AB,BC and AC respectively. What should be the value of F3 so that the total torque about O is zero?

View SolutionIf three forces −→F1,+−→F2and−→F3 are represented by three sides of a triangle and −→F1+−→F2=−−→F3 , then these three forces are concurrent forces and satisfy the condition for equilibrium .
Statement II : A triangle made up of three forces →F1,→F2and→F3 as sides taken in the same order ,satisfy the condition for translatory equilibrium . In the light of the above statements ,choose the most appropriate answer from the options given below :
View SolutionA vector →F1 is along the positive X-axis. If its vectors product with another vector →F2 is zero then →F2 could be
View SolutionA body is under the action of three forces →F1,→F2 and →F3. In which case the body cannot undergo angular acceleration ? .
View SolutionThree forces →F1,→F2 and →F3 are simultaneously acting on a particle of mass 'm' and keep it in equlibrium. If →F1 force is reversed in direction only, the acceleration of the particle will be.
View Solution
