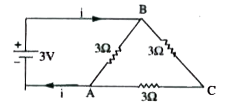
(a) Calculate $I_{1} and I_{2}$ in terms of I as shown in Fig(i)
(b) Calculate $V_{1} and V_{2}$ in terms of V as shown in Fig (ii).

Text Solution

Verified by Experts

(a) Current distribution in parallel Using junction law we can write
$I = I_{1} + I_{2}$ …(i)
$R_{1} and R_{2}$ are connected in parallel, hence the potential difference must be the same for both.
$I_{1} R_{1} = I_{2} R_{2} \Rightarrow I_{2} = I_{1} \frac{R_{1}}{R_{2}}$ ...(ii)
On substituting $I_{2}$ from equation (ii) in equation (i)
$I_{1} + I_{1} \frac{R_{1}}{R_{2}} = I$
$\Rightarrow I_{1} = \frac{R_{2}}{R_{1} + R_{2}} I$
Substituting $I_{1}$ in equation (ii)
$\Rightarrow I_{2} = \frac{R_{1}}{R_{1} + R_{2}} I$
The current is distributed inversely proportional to resistances in parallel
(b) Voltage distribution in series Let I be the common current flowing through both resistors. Voltage is distributed between two resistors connected in series
$V = V_{1} + V_{2}$ ...(iii)
$I = \frac{V}{R_{1} + R_{2}}$ ..(iv)
$V_{1} = I R_{1} = \frac{V R_{1}}{R_{1} + R_{2}}$
$V_{2} = I R_{2} = \frac{V R_{2}}{R_{1} + R_{2}}$
The potential difference is distributed directly proportional to resistances in series.

|

Updated on:21/07/2023

Class 12 PHYSICS CURRENT ELECTRICITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Current $I_{1} and I_{2}$ flow in the wires shown in Fig. The field is zero at distance x to the right of O. Then

A $x = (\frac{I_{1}}{I_{2}}) a$
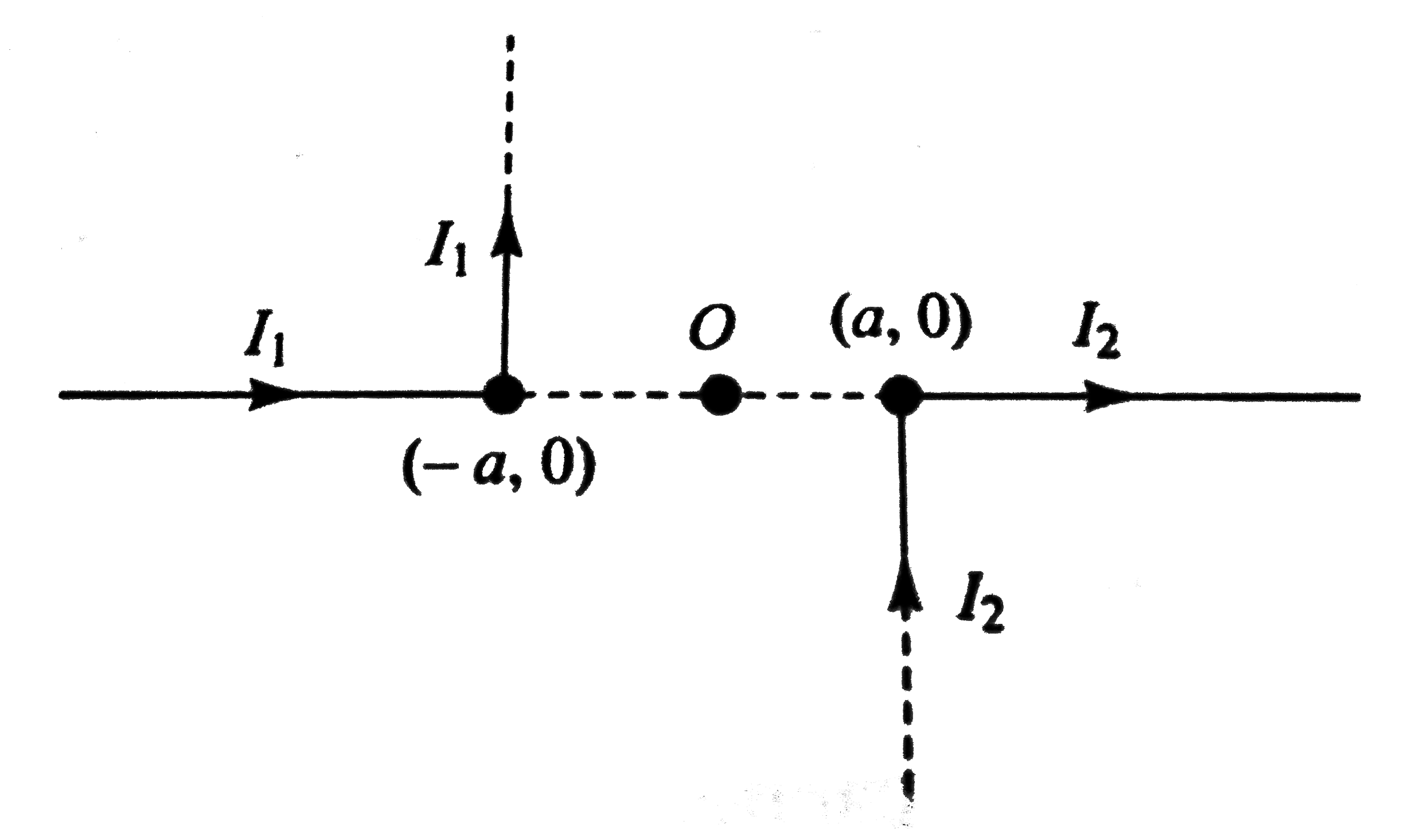B $x = (\frac{I_{2}}{I_{1}}) a$
C $x = (\frac{I_{1} - I_{2}}{I_{1} + I_{2}}) a$
D $x = (\frac{I_{1} + I_{2}}{I_{1} - I_{2}}) a$

MODERN PUBLICATION-CURRENT ELECTRICITY-TOUGH AND TRICKY PROBLEMS

Home
Ask Doubt
Profile