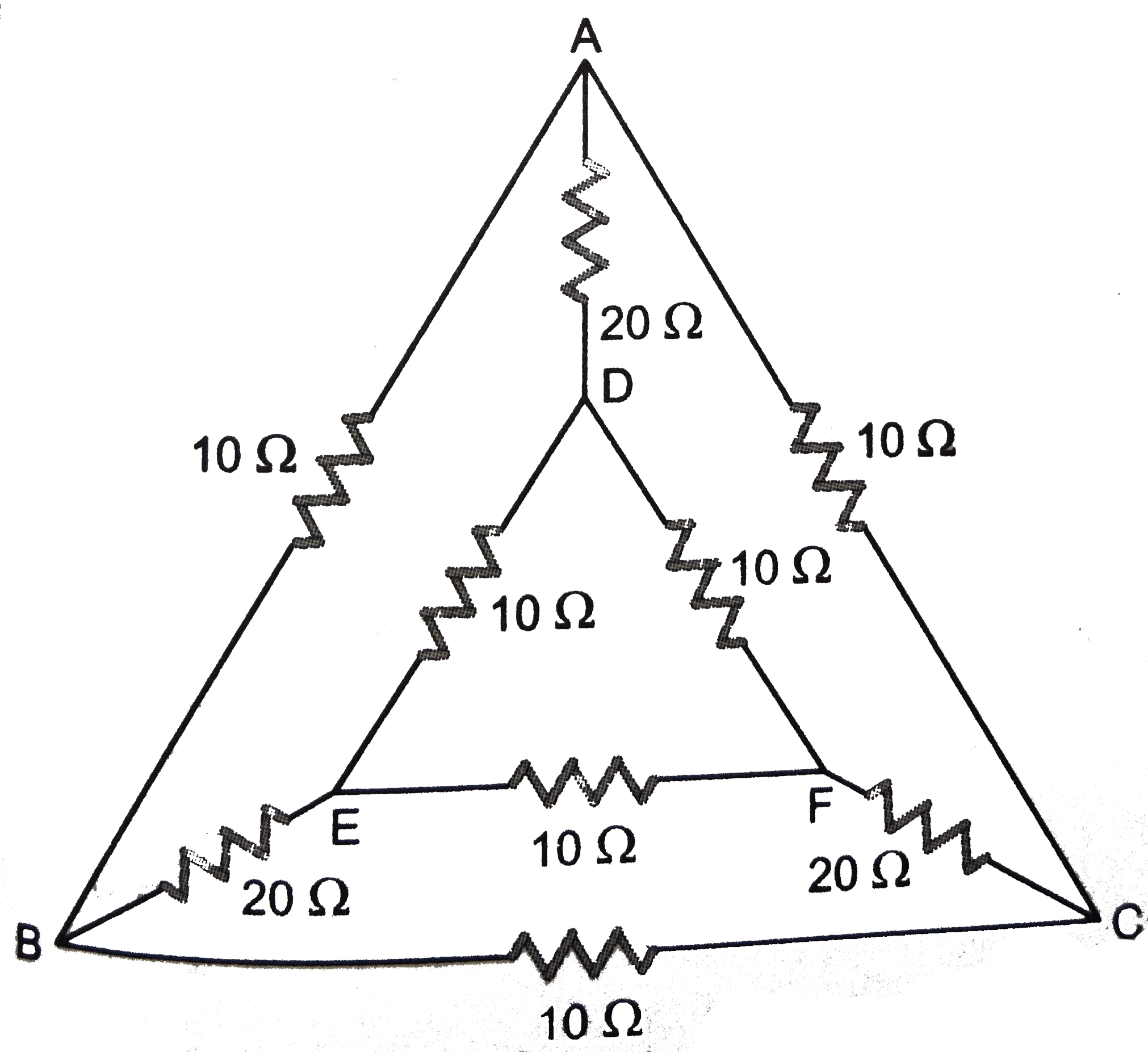The resistance of all the resistors in the following network is R. Find the equivalent resistance between A and F.

Text Solution
See figure to understand that points C and D are short circuited, so any resistor if connected between these two points is useless because no electric current will pass through it. Electric current always look for a path with the least resistance. If there is a zero resistance path, then all current must pass through this path. Two resistors are connected in parallel between points B and C. Similarly two other resistances are connected in parallel between D and E. Finally these four parts are connected in series with each other.
Req=R+R2+R2+R⇒Req=3R
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Textbook Exercises)
13 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Additional Exercises)
11 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - CONCEPTUAL QUESTIONS
35 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Knowledge Check
Each of the resistor shown in fig. has resistance R. Find the equivalent resistance between A and B
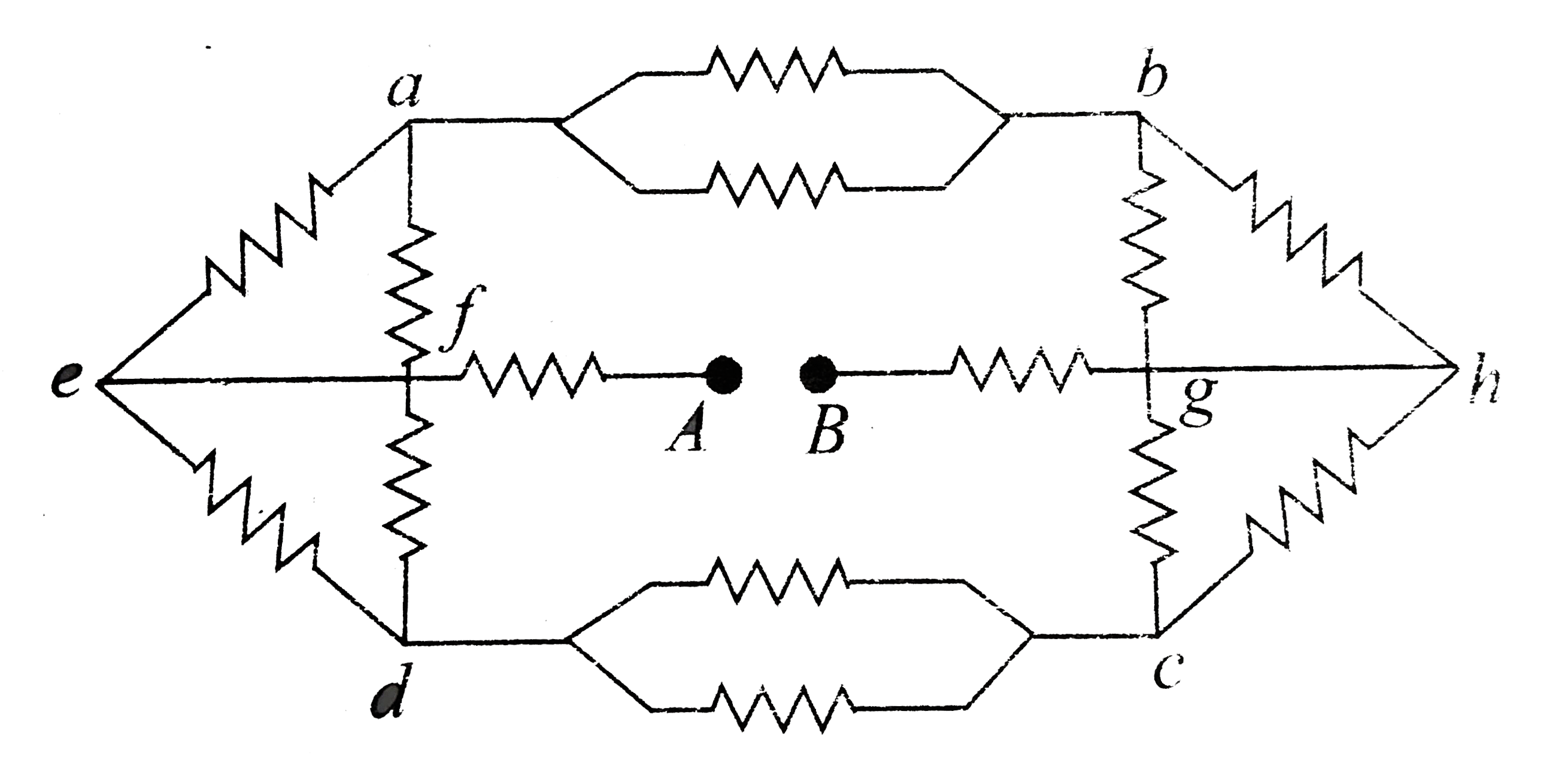 A7R4B5R4C9R4D11R4
A7R4B5R4C9R4D11R4If each of the resistance in the network in figure R, the equivalent resistance between terminals A and B is
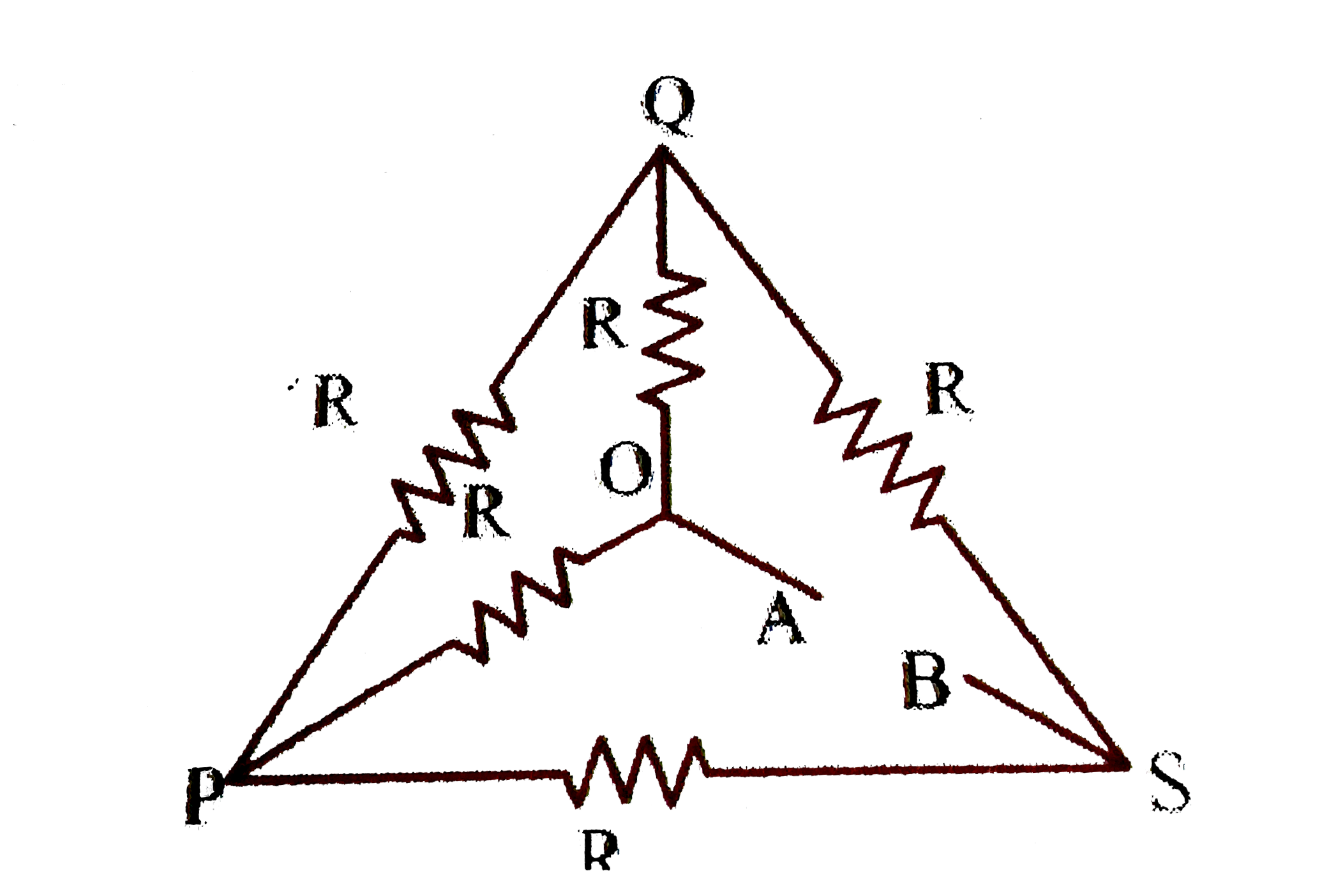 A5RB2RC4RDR
A5RB2RC4RDR
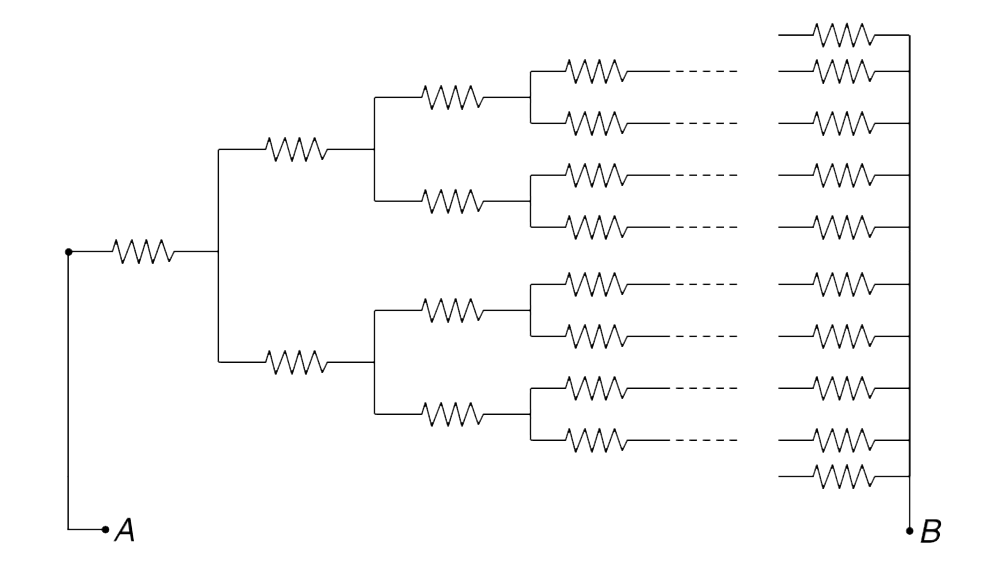
An infinite network of resistances has been made as shown in the figure. Each resistance is R. find the equivalent resistance between A and B.
View SolutionIf each of the resistance in the network in figure R,
the equivalent resistance between terminals A and B is
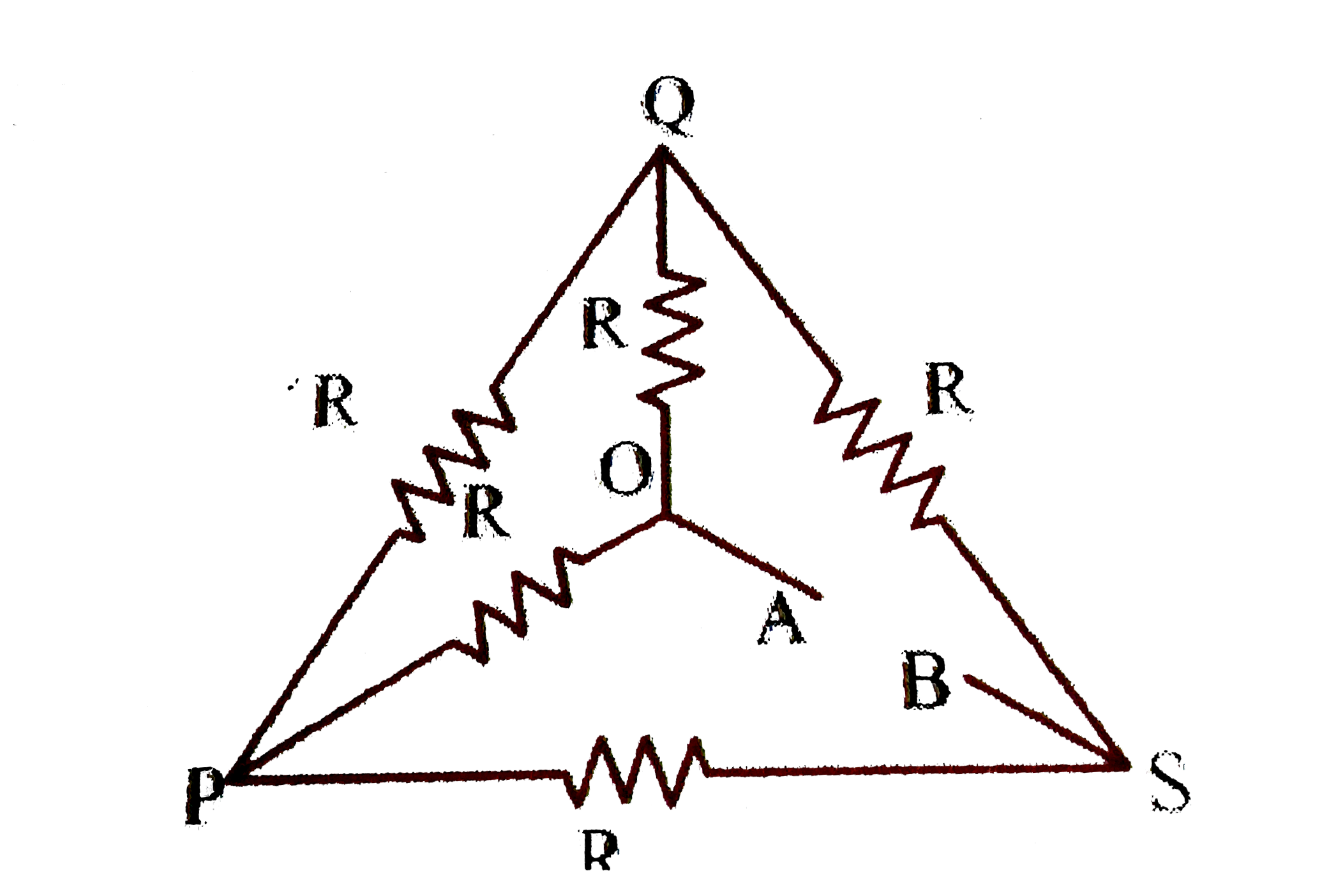
View SolutionIf each of the resistance in the network in figure R,
the equivalent resistance between terminals A and B is
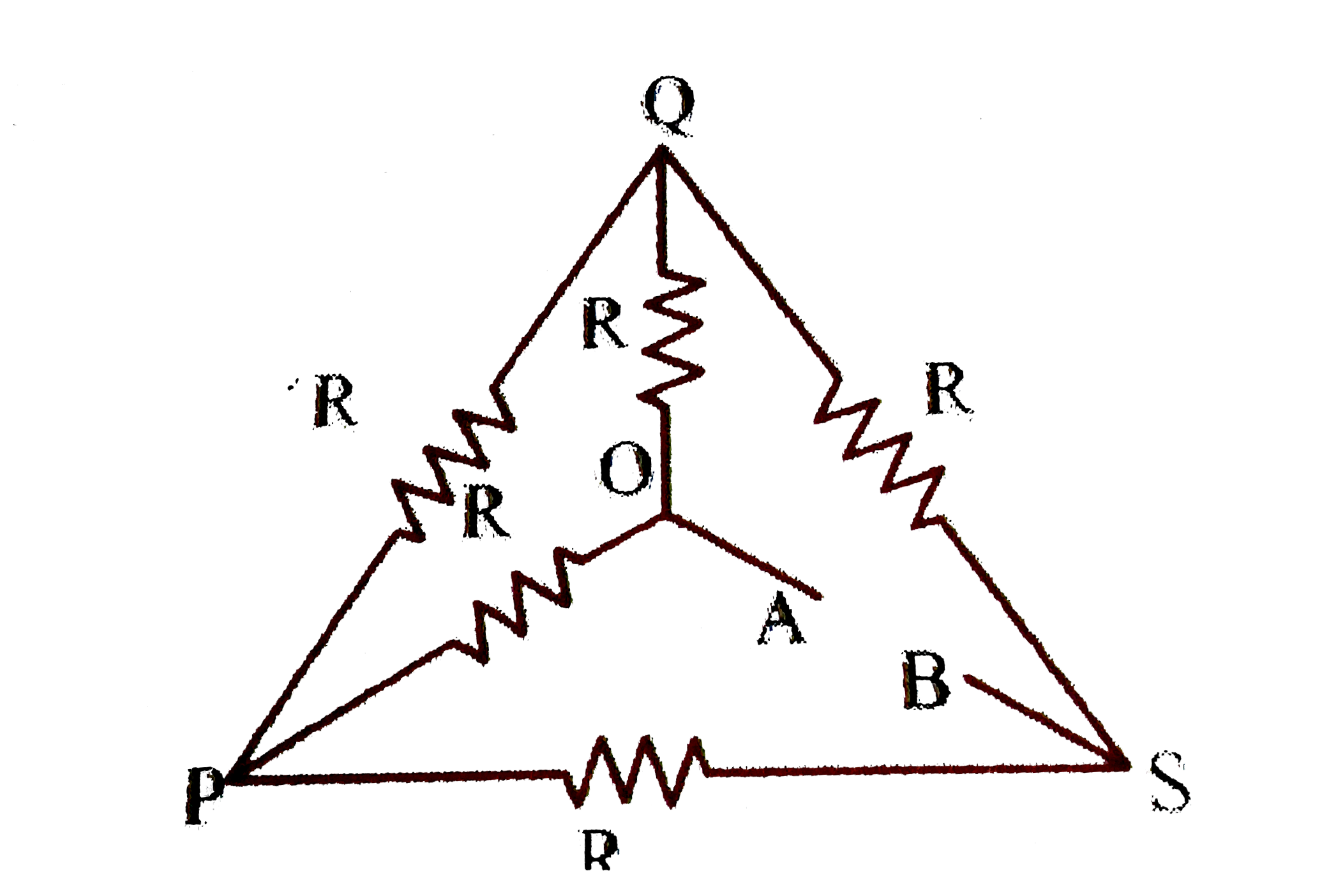
View SolutionFind in the given network of resistors, the equivalent resistance between the points A and B
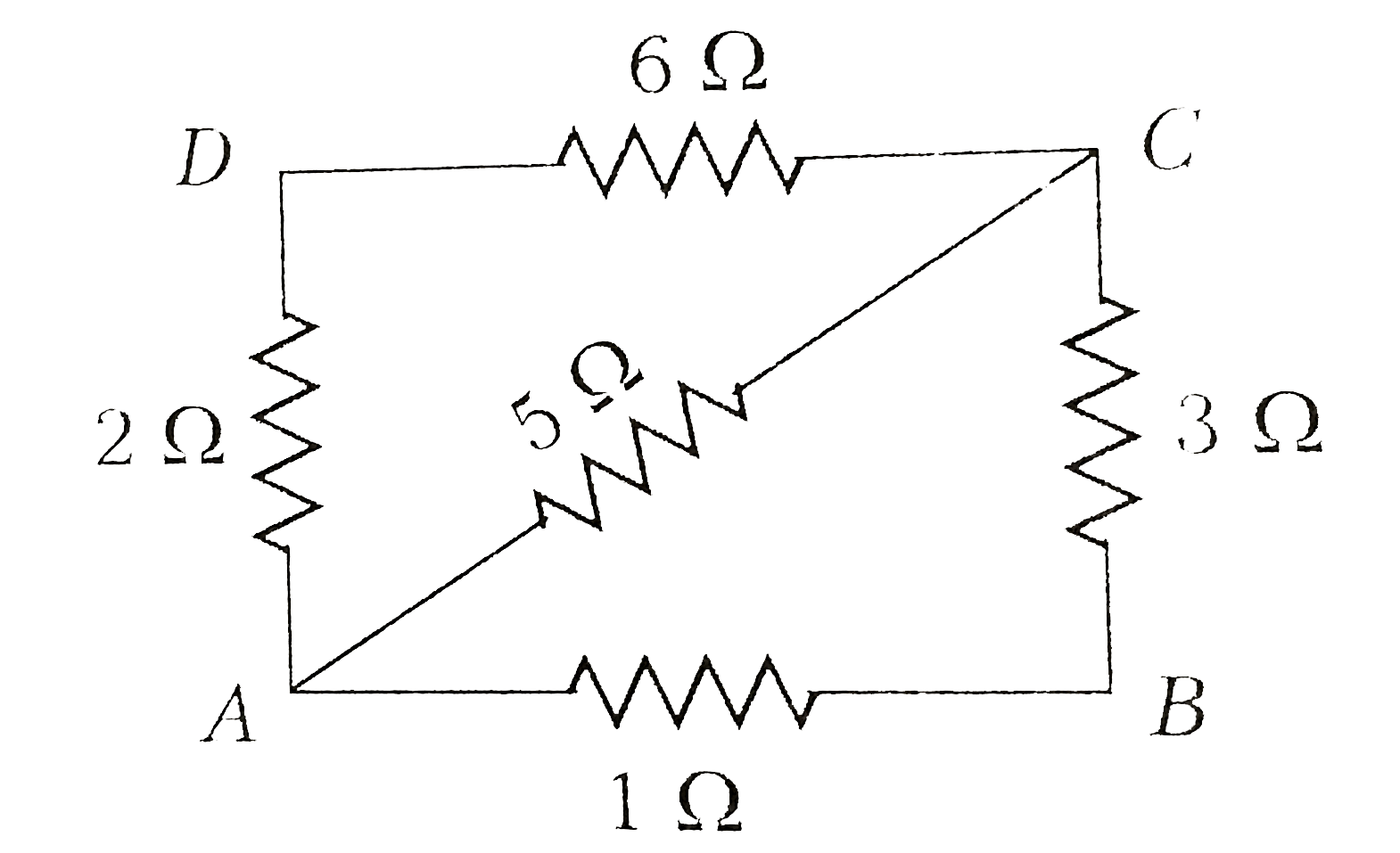
View SolutionIn the network shown in fig. each resistance is R.

The equivalent resistance between A and C is
View SolutionIn the network shown, each resistance is R. Calculate the equivalent resistance between A and B.
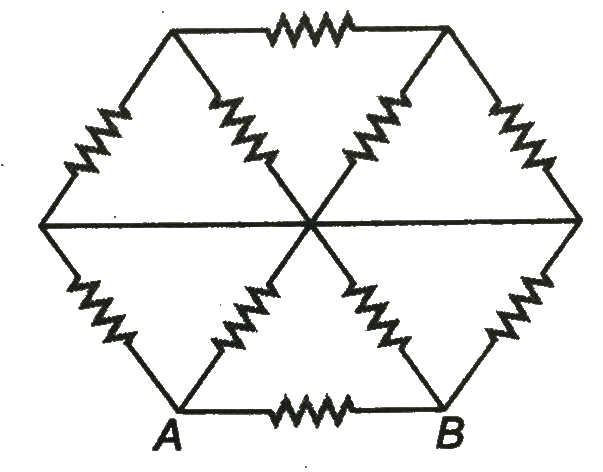
View Solution