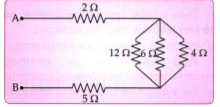
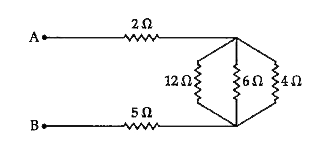
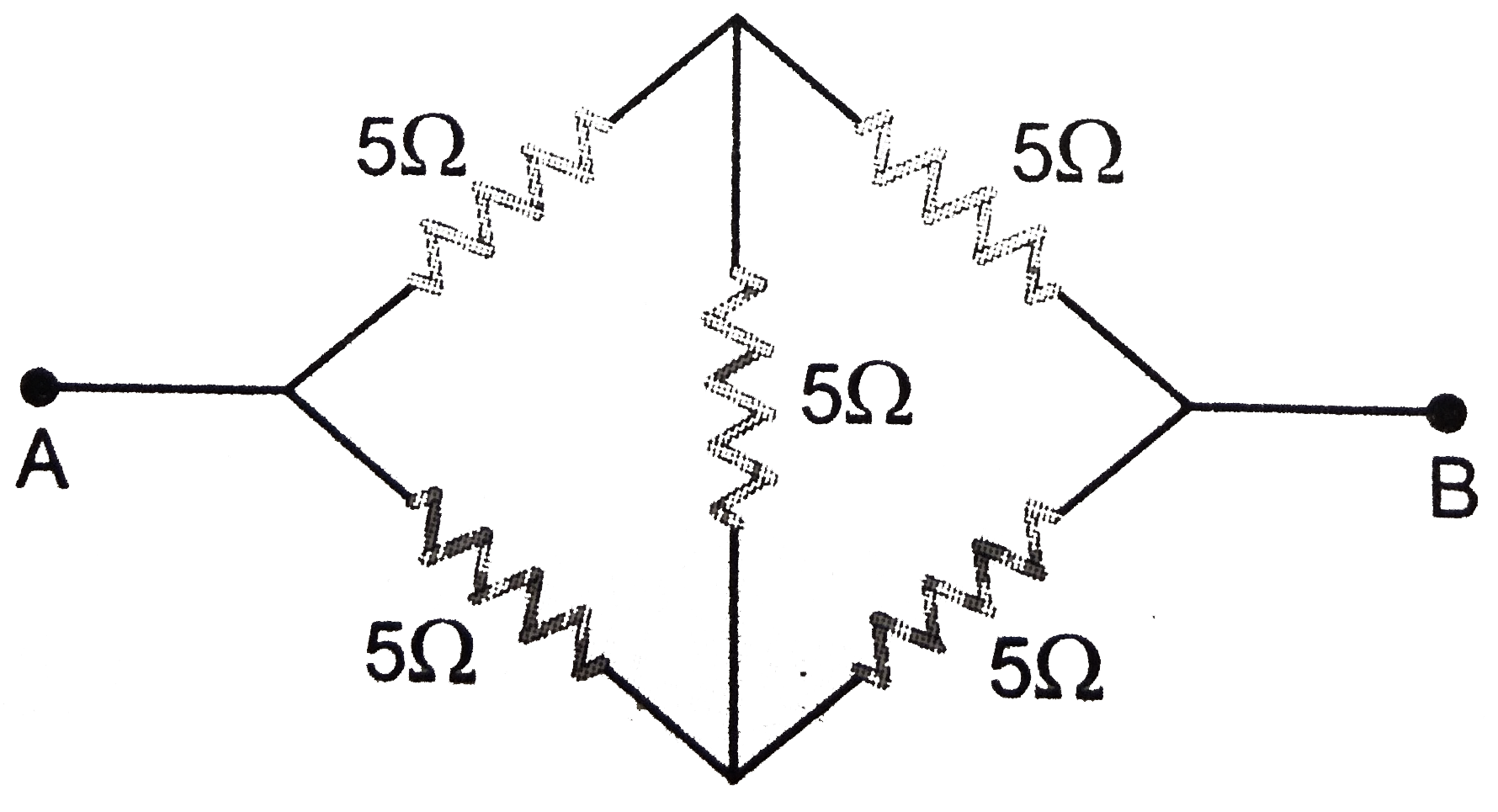
Find the current in the branch BD of the following circuit. Also calculate the equivalent resistance between points A and B .

Text Solution
Using Kirchhoff.s loop law we can formulate equations to find electric current in various branches. While distributing current in the circuit, we have assumed 3 unknowns, hence require at least three equations.
Loop ABCEFGA:
−2I1−2(I1−I2)−I+12=0⇒4I1−2I2+I=12 ...(i)
Loop ABDA: −2I1−I2+(I−I1)=0⇒3I1+I2=I ...(ii)
Loop BCDB: −2(I1−I2)+2(I−I1+I2)+I2=0⇒4I1−5I2=2I ...(iii)
On solving equations (ii) and (iii) we get
I1=7I19&I2=−2I19 ...(iv)
On substituting values from equation (iv) in equation (i), we get
I=7617A ...(v)
On substituting equation (v) in equation iv, we get
I1=2817AandI2=−817A ...(vi)
Now let us see the equivalent resistance between A and C. Here V=12 volts adn the battery is supplying a total current of I= 76/17 A. According to Ohm.s law total resistance of the circuit must be V/I.
Rtotal=VI=12×1776=3×1719⇒Rtotal=5119Ω ...(vii)
This total resistance include internal resistance of the battery also. Let R be the equivalent resistance between A and B. It is connected in series with the internal resistance 1Ω of the battery, hence:
R+1=5119⇒R=3219Ω
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Textbook Exercises)
13 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Additional Exercises)
11 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - CONCEPTUAL QUESTIONS
35 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Knowledge Check
Find the equivalent resistance between the points a and b
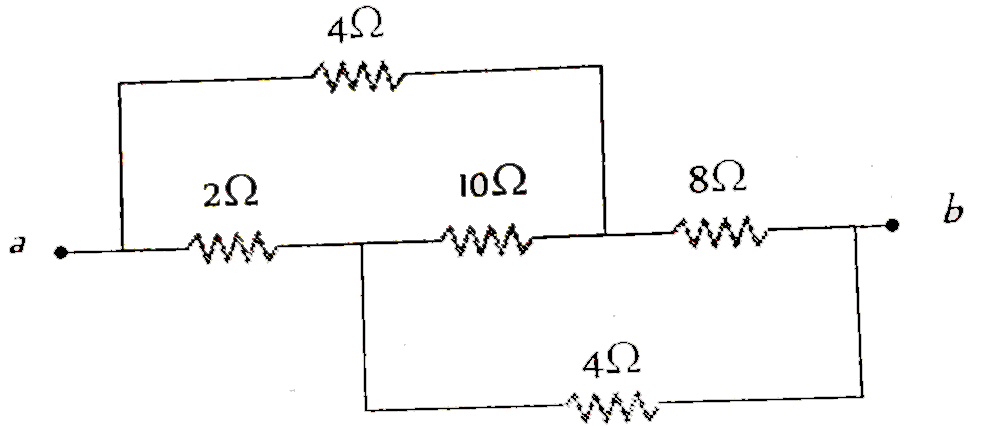 A2ΩB4ΩC8ΩD16Ω
A2ΩB4ΩC8ΩD16ΩFind the equivalent resistance between points A and B in the following circuit
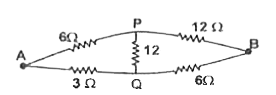 A6ΩB12ΩC4ΩD18Ω
A6ΩB12ΩC4ΩD18Ω
Find the equivalent resistance between point A and B
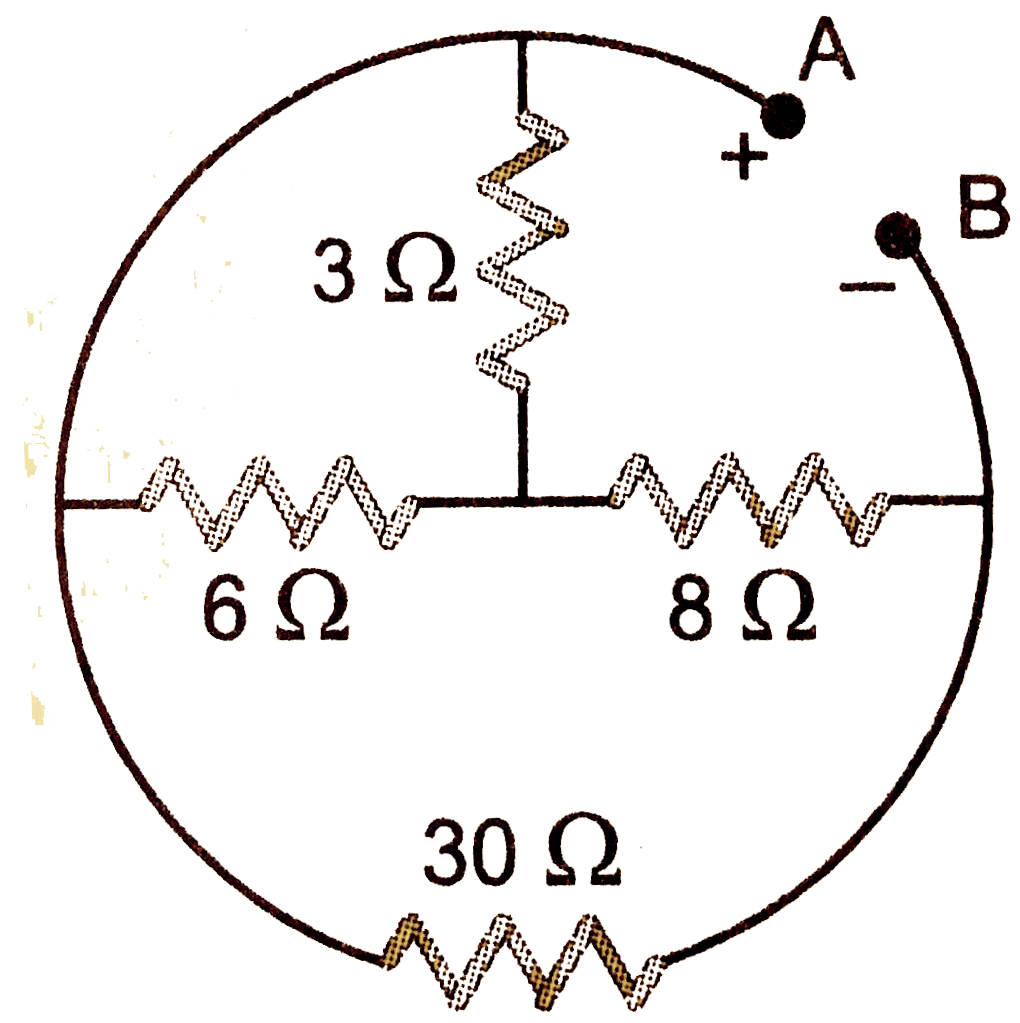
View SolutionFind the equivalent resistance between points A and B

View SolutionCalculate the equivalent resistance between the points A and B in Fig.
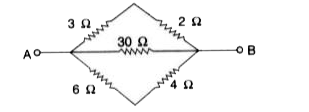
View SolutionFind the equivalent resistance between the points A and B.
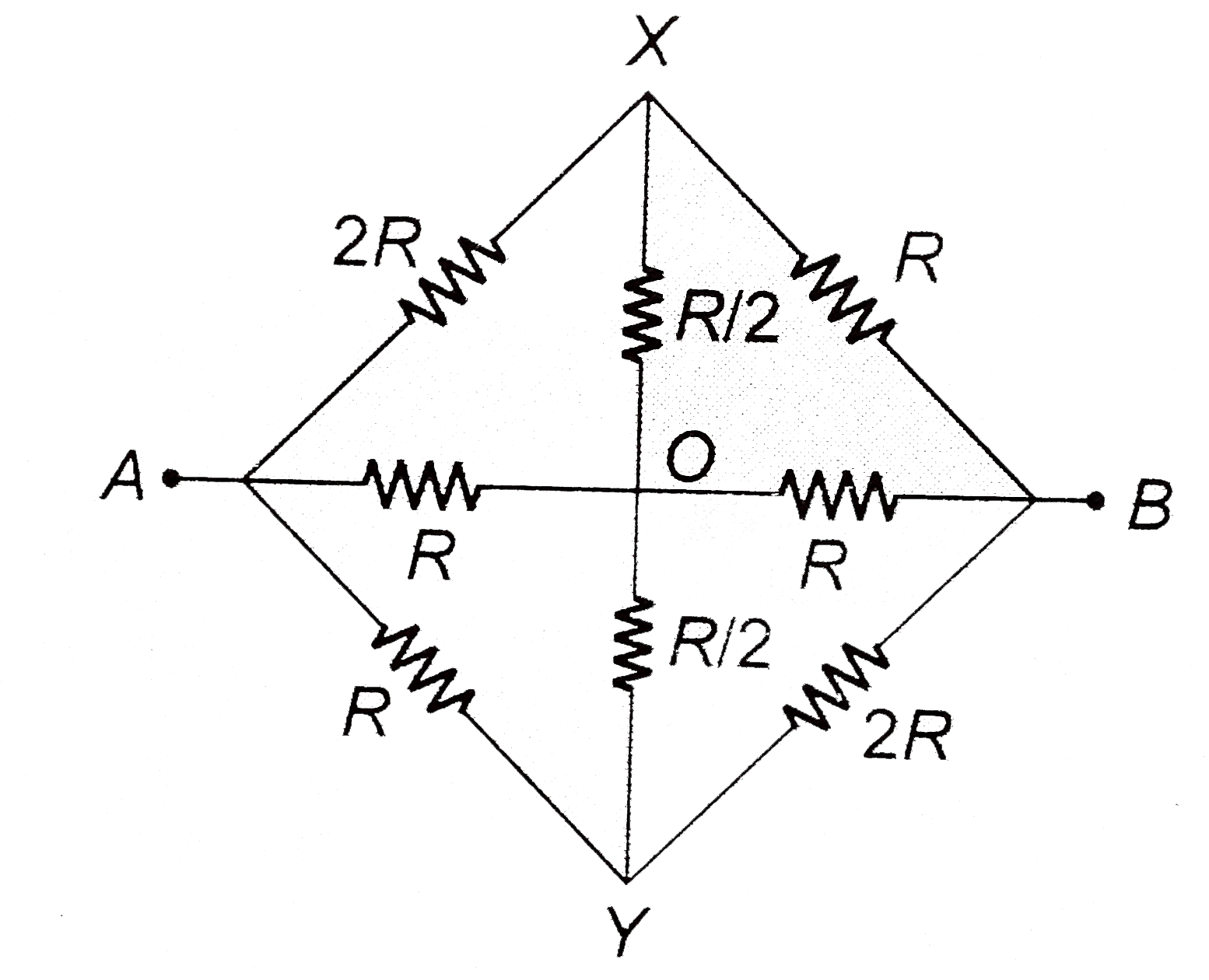 .
.
View SolutionFind the equivalent resistance between the point a and b .
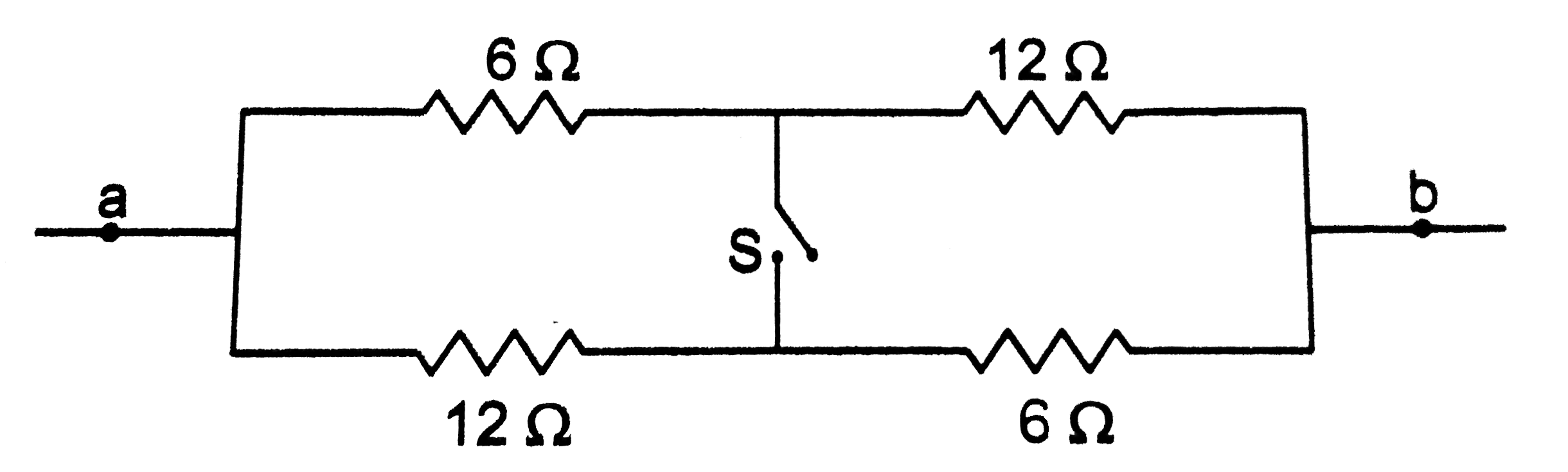
View SolutionWhat is the equivalent resistance between points A and B in the circuit.
View Solution