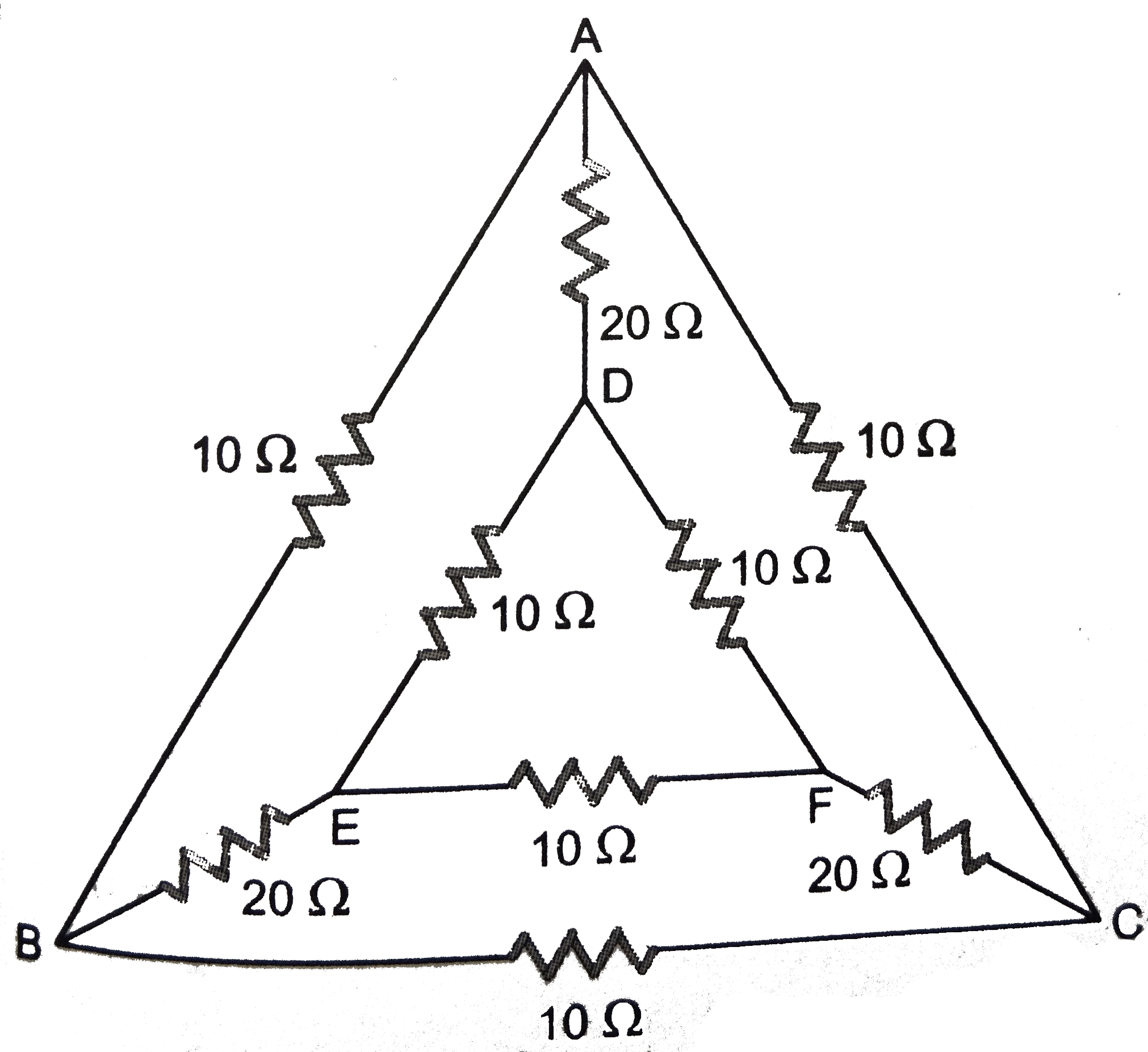The resistance of all the resistors in the following network is R . Find equivalent resistance between A and E .

Text Solution
At point B network is splitting in two identical halves, and hence, current 4I is equally divided in two parts. At point C and D two identical resistors are in parallel, so at these points also current is equally divided. Applying Dirchhoff.s law for loop EFABCE we get:
V−4IR−2IR−IR=0
⇒V=7IR
⇒VI=7R
⇒Req=V4I=7R4
You can easily find the answer using the series and parallel method. Also note that from B to C and from B to D, there is an equal potential drop. Hence, potential of point C and D must be same. If you consider points C and D at the same location then also the answer is going to remain the same.

Hence, net resistance:
Req=R+R2+R4rARrReq=7R4
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Textbook Exercises)
13 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Additional Exercises)
11 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - CONCEPTUAL QUESTIONS
35 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Knowledge Check
Each of the resistor shown in fig. has resistance R. Find the equivalent resistance between A and B
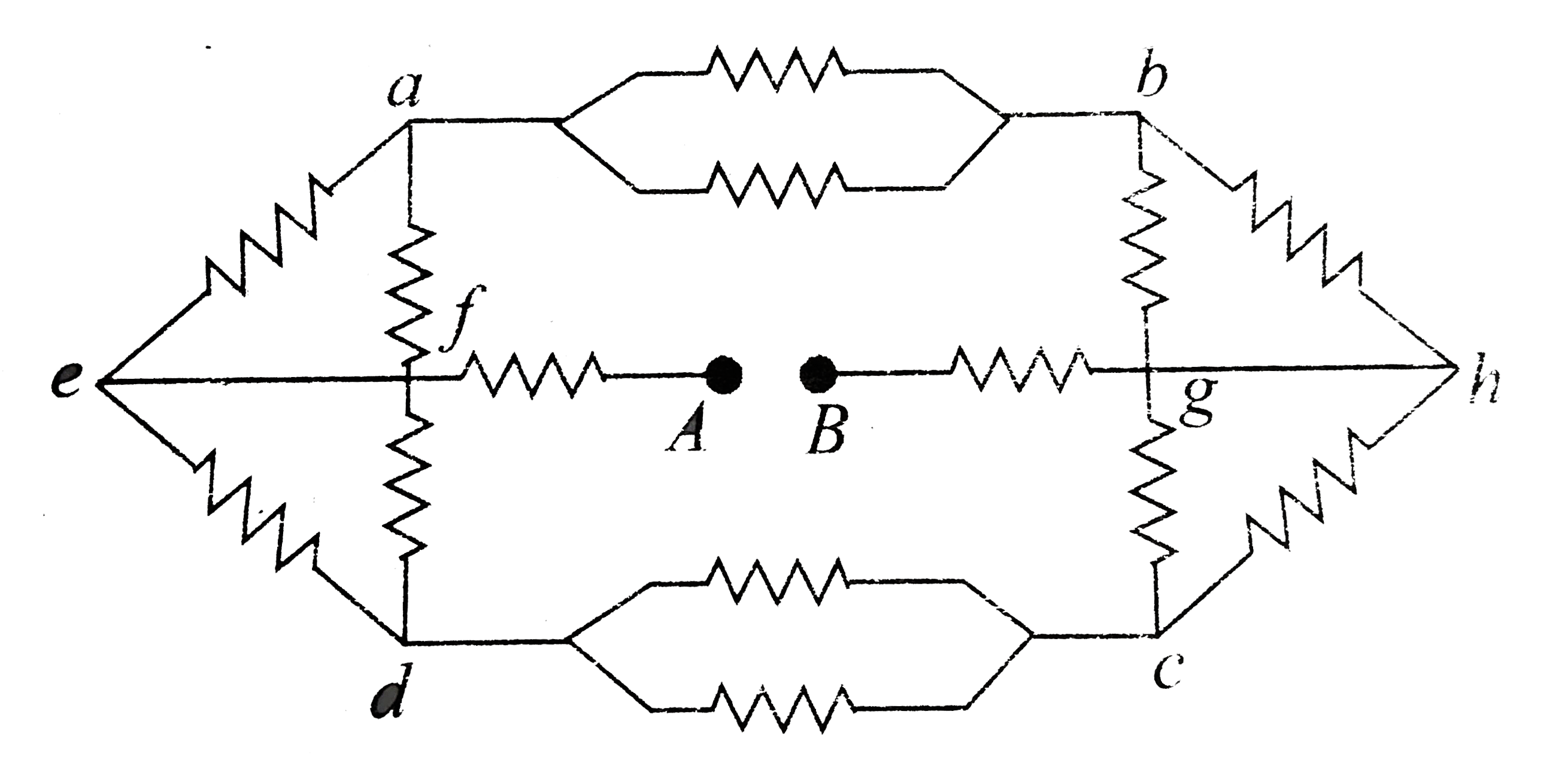 A7R4B5R4C9R4D11R4
A7R4B5R4C9R4D11R4If each of the resistance in the network in figure R, the equivalent resistance between terminals A and B is
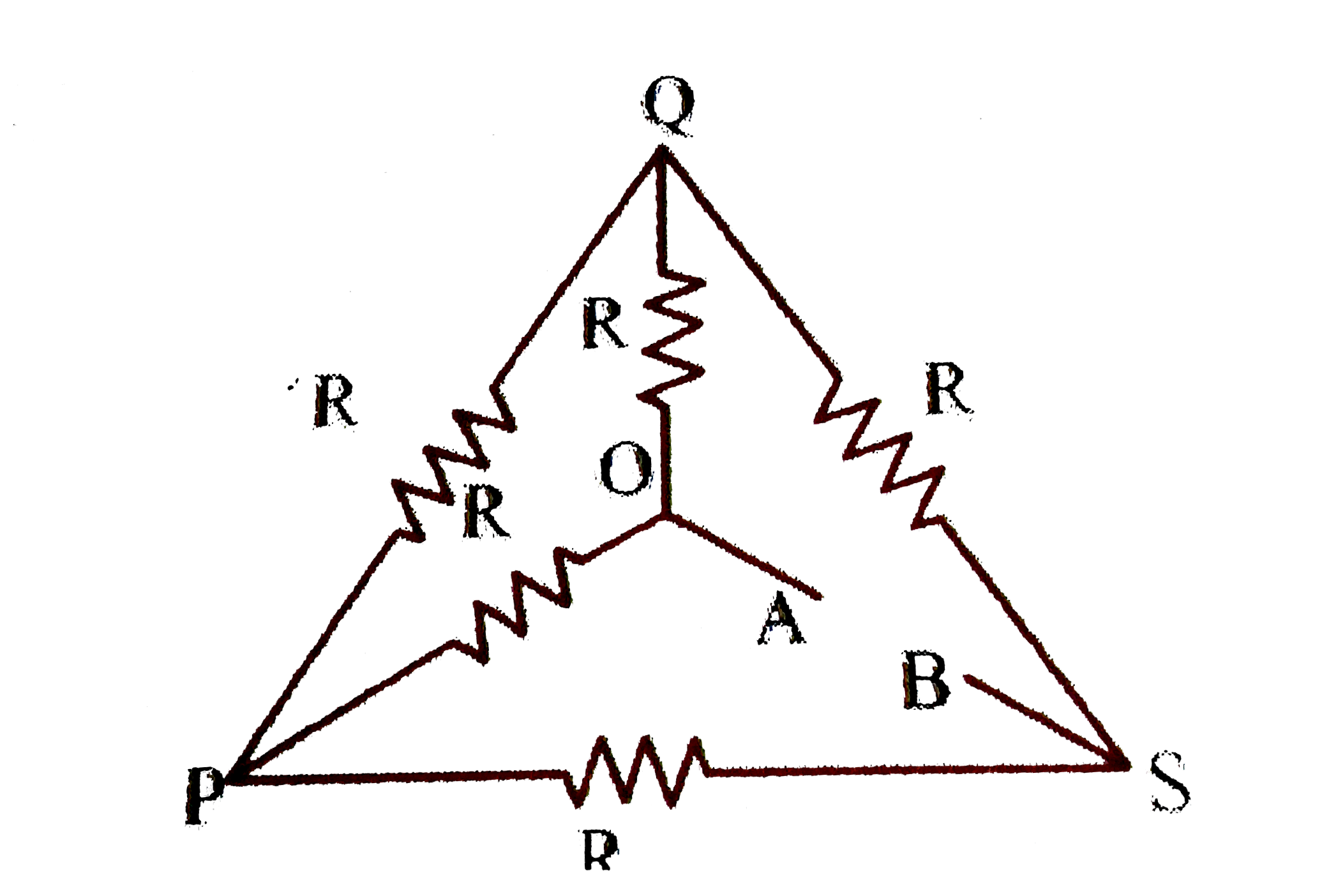 A5RB2RC4RDR
A5RB2RC4RDRSix resistors each of resistance R and two resistors each of resistance r are connected in the network shown below. The equivalent resistance between A and B is
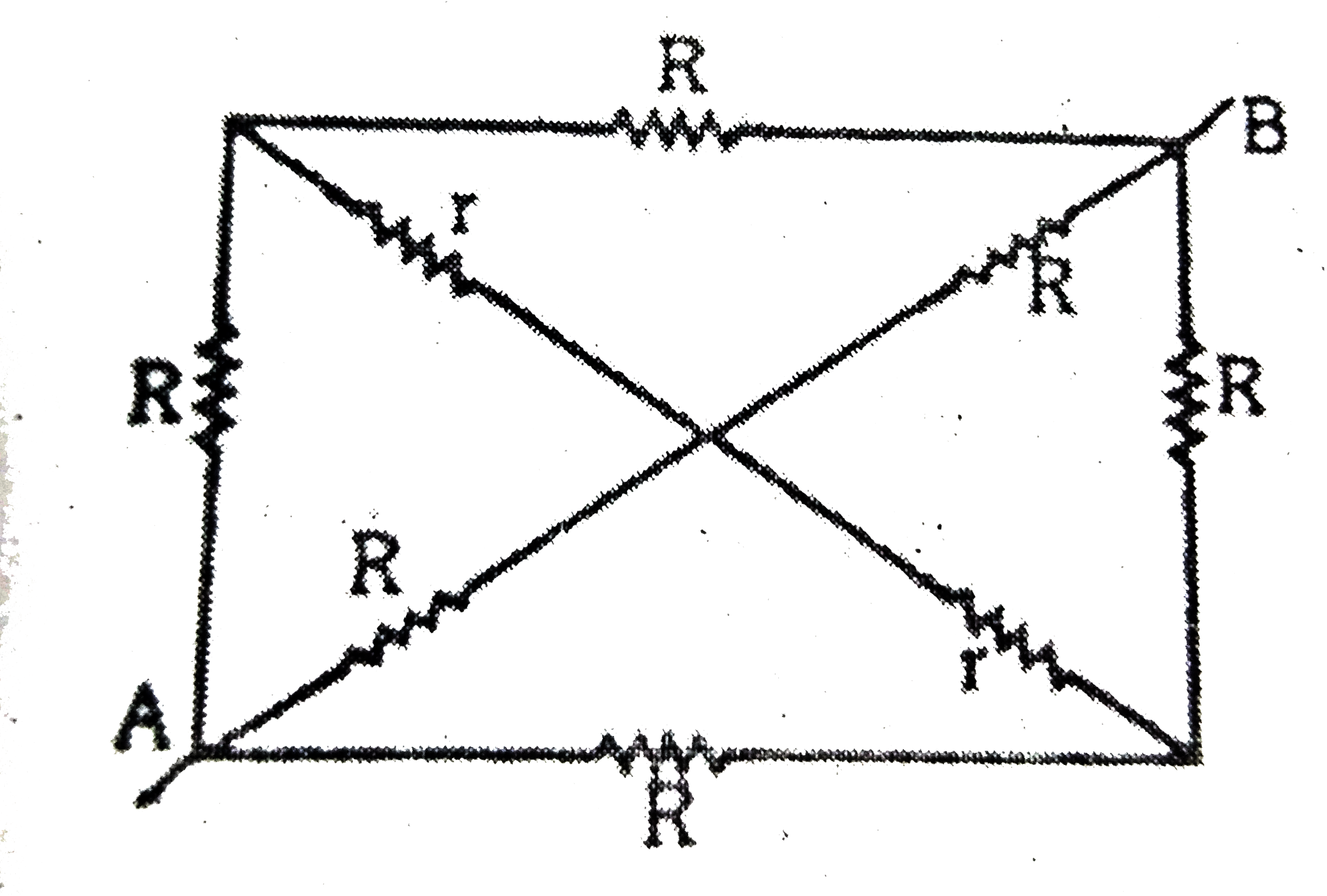 A3R+rB6R+2rC2R/3DR3+r3
A3R+rB6R+2rC2R/3DR3+r3
If each of the resistance in the network in figure R,
the equivalent resistance between terminals A and B is
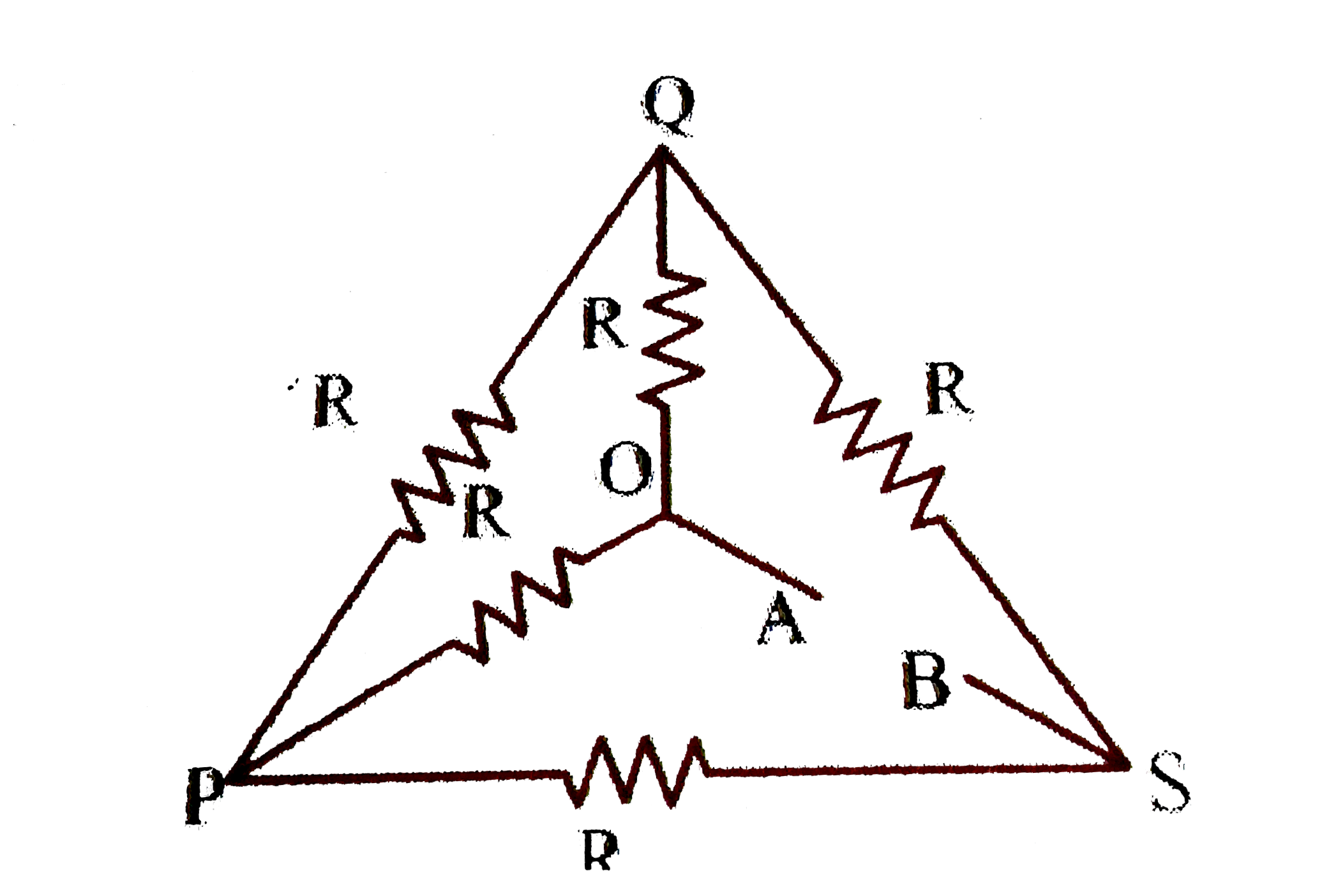
View SolutionIf each of the resistance in the network in figure R,
the equivalent resistance between terminals A and B is
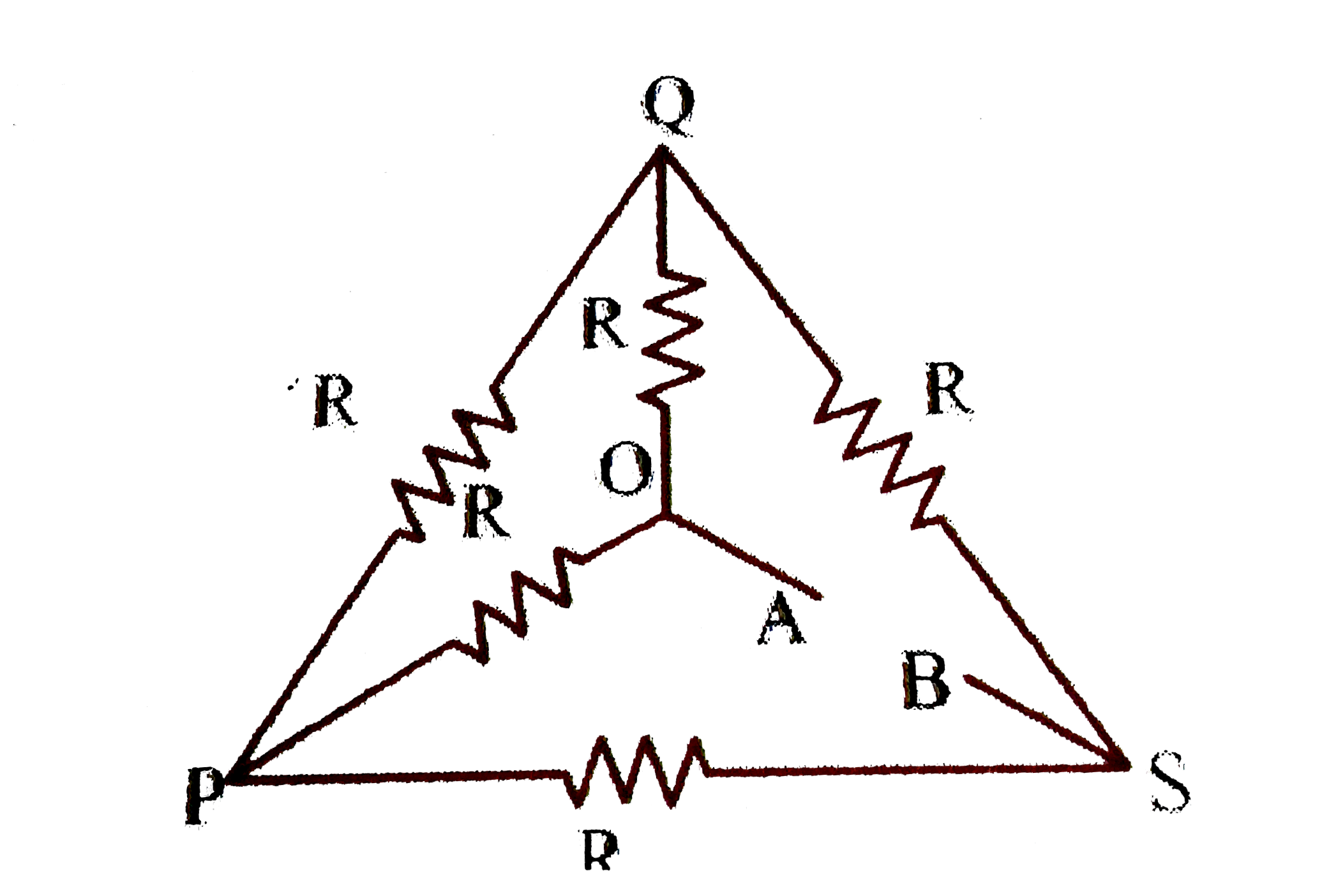
View SolutionSix resistors each of resistance R and two resistors each of resistance r are connected in the network shown below. The equivalent resistance between A and B is

View SolutionAn infinite network of resistances has been made as shown in the figure. Each resistance is R. find the equivalent resistance between A and B.
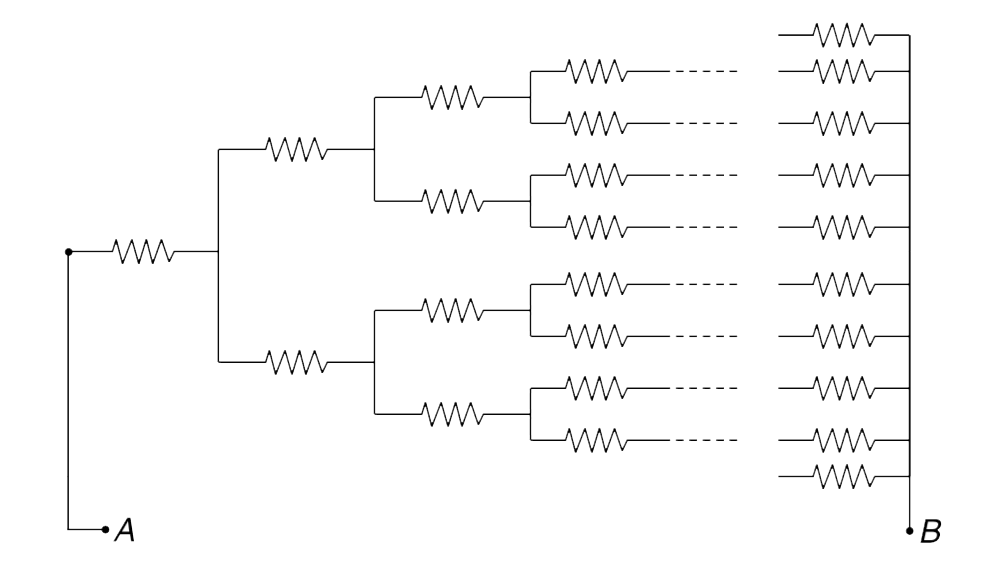
View SolutionIn the network shown in fig. each resistance is R.

The equivalent resistance between A and C is
View Solution