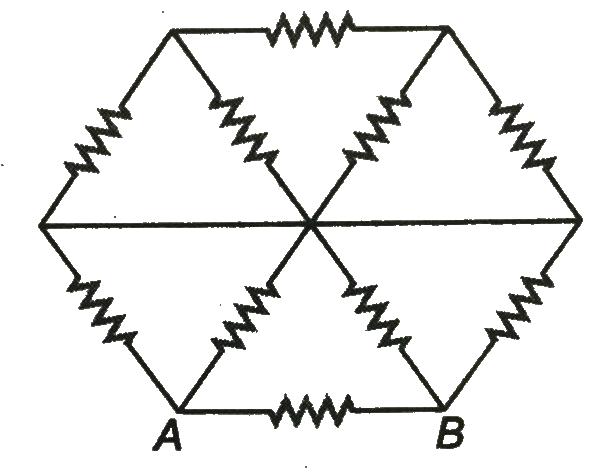
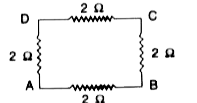
Here is one network of resistances as shown in the figure. An infinite number of similar links are there. Calculate the equivalent resistance between A and B.

Text Solution
If there are infinite number of similar branches then the equivalent resistance between A and B should not change by removing some links. Let us assume x is the equivalent resistance between A and B. If we remove the first two resistors then the equivalent resistance between C and D must be same as that between A and B. We can reduce the above problem as shown in below figure.

Finally the outcome is as follows: Resistances 2R and x are connected in parallel and then these two are connected with R in series to produce equivalent resistance equal to x. We can write the same thing in the form of equation as follows:
x=R+(2R)x2R+x⇒x=2R2+Rx+2Rx2R+x
⇒x2+2Rx=2R2+3Rx
⇒x2−Rx−2R2=0
⇒x=R±√R2+8R22=R±3R2
Here, x should be positive. Hence, the answer is x= 2R.
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Textbook Exercises)
13 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Additional Exercises)
11 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - CONCEPTUAL QUESTIONS
35 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Knowledge Check
In the network shown, the equivalent resistance between A and B is
 A43ΩB34ΩC2417ΩD1724Ω
A43ΩB34ΩC2417ΩD1724ΩIn the network shown below, the equivalent resistance between A and B is
 AR/2BRC2RD4R
AR/2BRC2RD4RIn the network shown in the figure, the equivalent resistance between A and C is
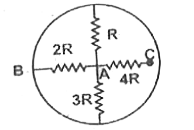 A10 RB(6/11)RC(12/15)RD(50/11)R
A10 RB(6/11)RC(12/15)RD(50/11)R
In the network shown in the figure, the equivalent resistance between A and C is

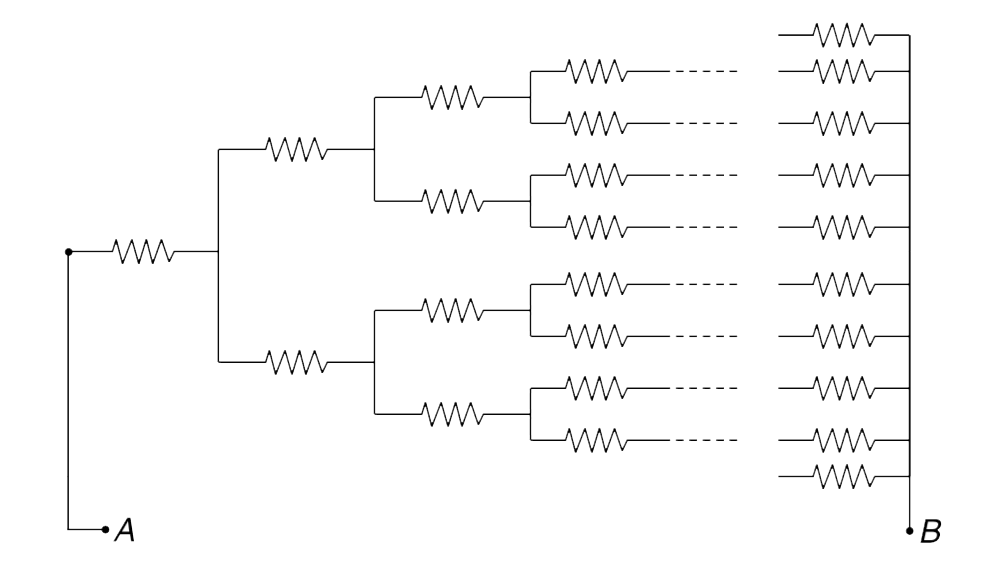
View SolutionAn infinite network of resistances has been made as shown in the figure. Each resistance is R. find the equivalent resistance between A and B.
View SolutionIn the network shown in Fig., calculate the equivalent resistance between the points
A and B,
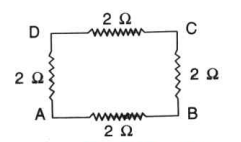
View SolutionIn the network shown in Fig., calculate the equivalent resistance between the points
A and C.
View SolutionIn the network of resistors shown in the adjoining figure, the equivalent resistance between A and B is

View Solution