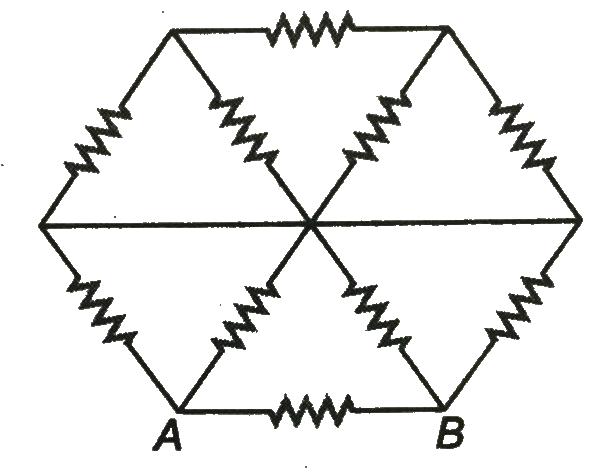
Here is one network of resistances as shown in the figure. An infinite numbers of links are present. The magnitude of resistances in every subsequent link is doubled. Calculate the equivalent resistance between A and B.

Text Solution
In this example, if we start from C and D instead of A and B, then equivalent resistance must be doubled. If x is the equivalent resistance between A and B then 2x will be the equivalent resistance between C and D. So the above network can be reduced as follows:

Resistance 2R adn 2x are connected in parallel with each other and this combination is connected in series with R, to produce the net resistance x.
x=R+4Rx2R+2x
⇒x=R+2RxR+x=R2+Rx+2RxR+x
⇒xR+x2=R2+Rx+2Rx
⇒x2−2Rx−R2=0
⇒x=2R±√4R2+4R22
⇒x=R±R√2
⇒x=R(1+√2) (Leaving out the negative answer)
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Textbook Exercises)
13 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Additional Exercises)
11 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - CONCEPTUAL QUESTIONS
35 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Knowledge Check
In the network shown below, the equivalent resistance between A and B is
 AR/2BRC2RD4R
AR/2BRC2RD4RIn the network shown, the equivalent resistance between A and B is
 A43ΩB34ΩC2417ΩD1724Ω
A43ΩB34ΩC2417ΩD1724ΩIn the network shown in the figure, the equivalent resistance between A and C is
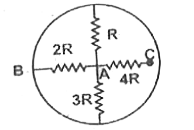 A10 RB(6/11)RC(12/15)RD(50/11)R
A10 RB(6/11)RC(12/15)RD(50/11)R
In the network shown in Fig., calculate the equivalent resistance between the points
A and B,
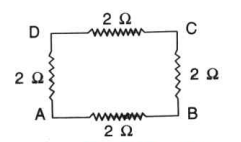
View SolutionIn the network shown in Fig., calculate the equivalent resistance between the points
A and C.
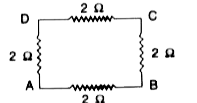
View SolutionIn the network shown in the figure, the equivalent resistance between A and C is

View SolutionIf each of the resistance in the network in figure R,
the equivalent resistance between terminals A and B is
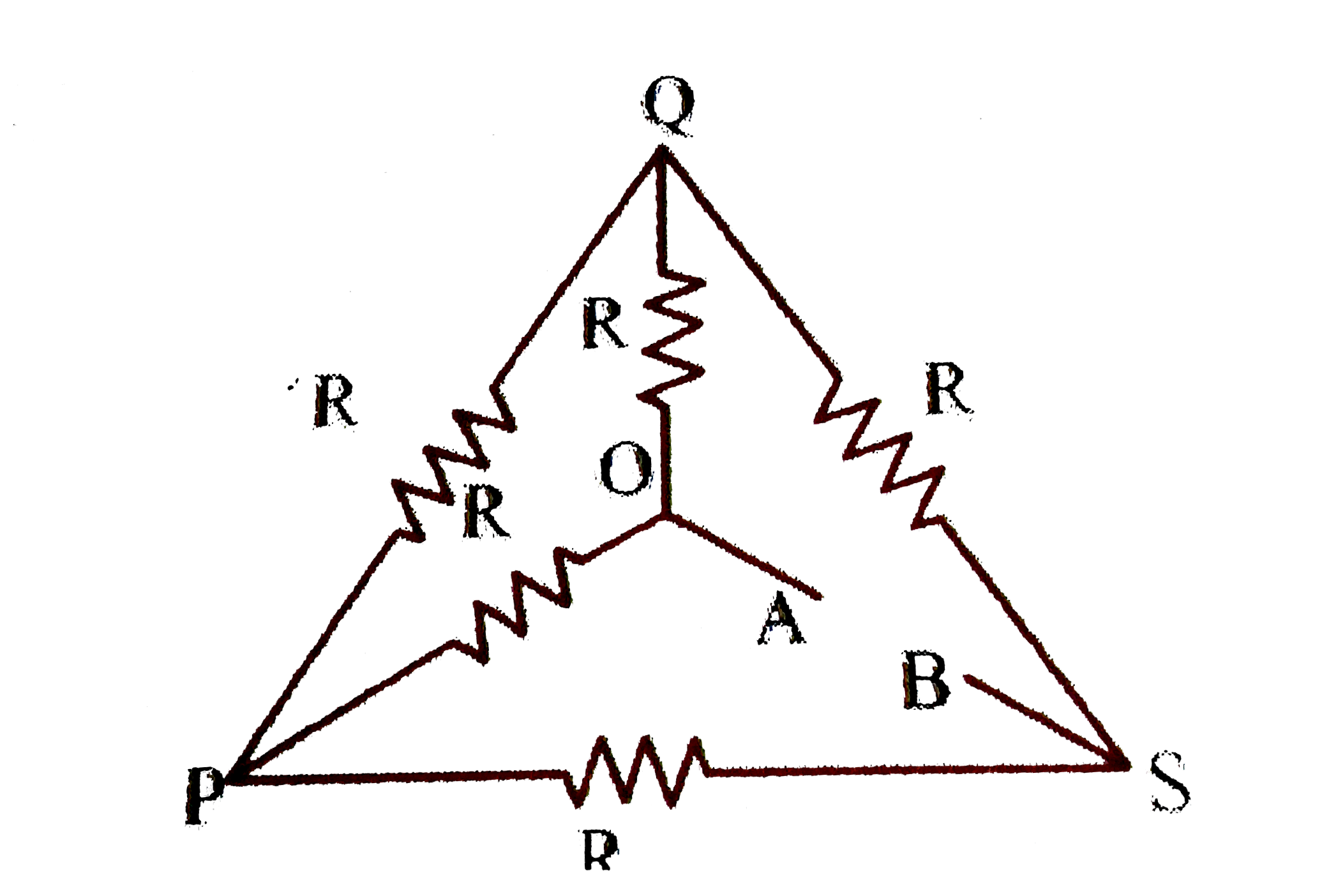
View SolutionIf each of the resistance in the network in figure R, the equivalent resistance between terminals A and B is
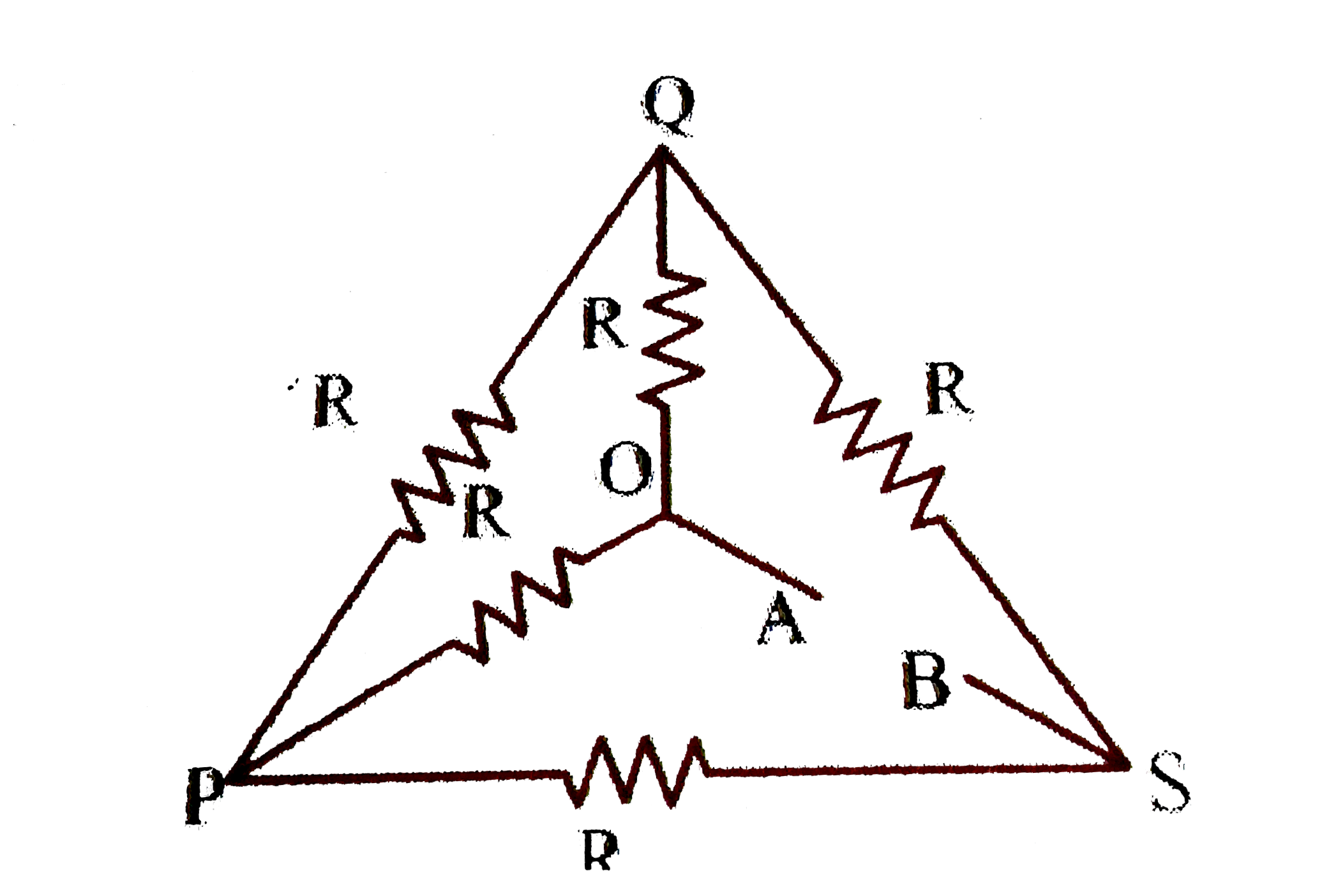
View Solution