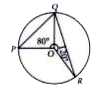
In the given figure, O is the centre of a circle C(O,r) and PO bisects ∠APC . Prove that AB=CD.
Video Solution
Text Solution
Draw OE⊥AB and OF⊥CD.
Now, in ΔOEP and ΔOFP we have
∠OEP=∠OFP [ each equal to 90∘]
∠OPE=∠OPF[ given ]
OP=OP [common]
∴ΔOEP≅ΔOFP[ AAS-congruence ]
⇒OE=OF [c.p.c.t.]
⇒ chords AB and CD are equidistnat from the centre O
⇒AB=CD [ chords equidistant from the centre are equal ].
Hence, AB=CD
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A22videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B18videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B16videos
BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGON
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)20videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, O is the centre of the circle. The value of x is
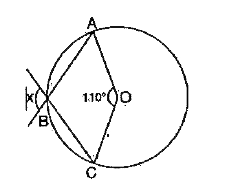 A75∘B55∘C125∘D110∘
A75∘B55∘C125∘D110∘ - Question 2 - Select One
In the given figures, value of y (O is the centre of the circle) is
 A100∘B120∘C130∘D140∘
A100∘B120∘C130∘D140∘
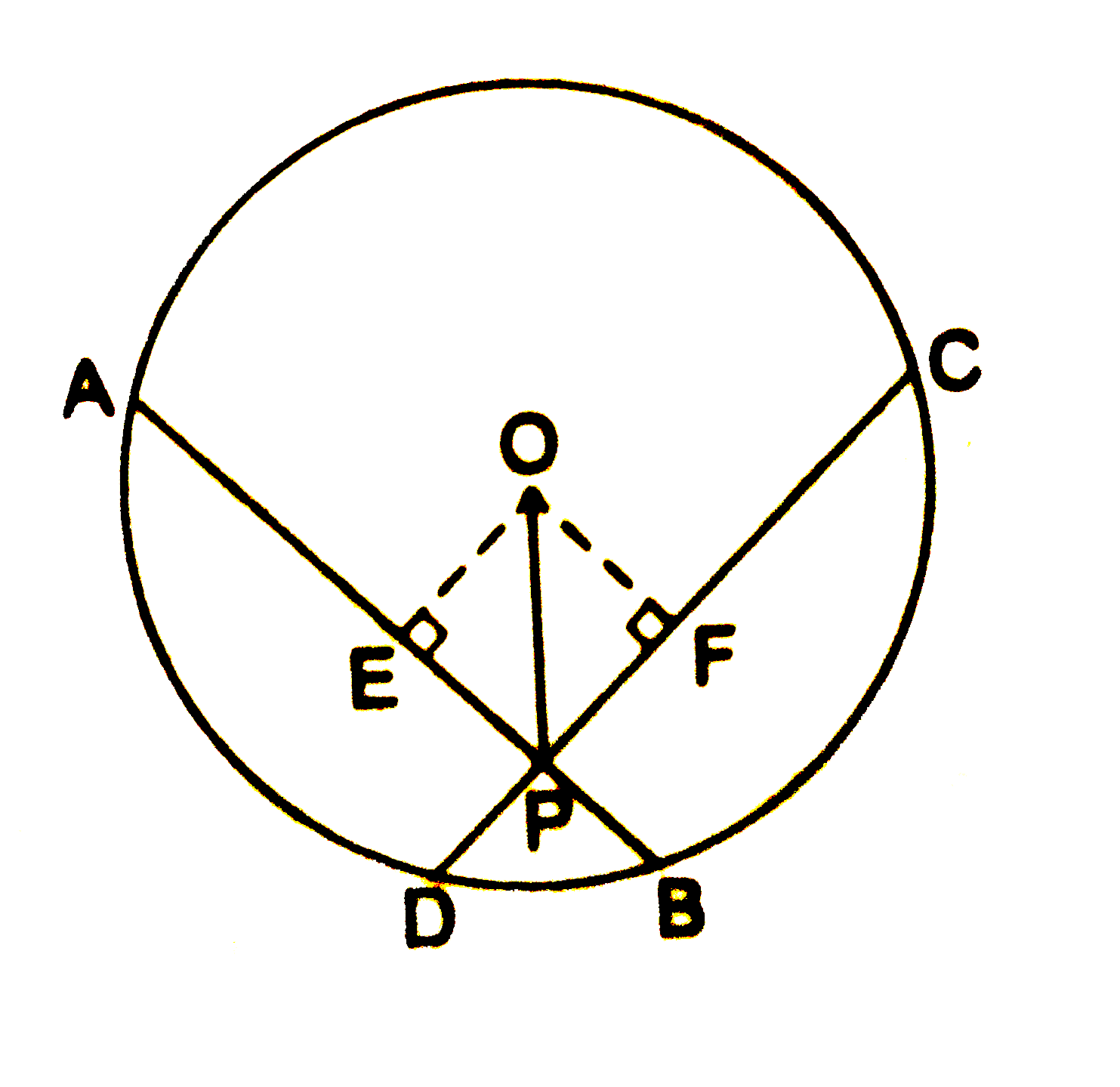
In Figure, O is the center of a circle and PO bisects ∠APD Prove that AB=CD
 View Solution
View SolutionIn Figure, AB=CB and O is the centre of the circle. Prove that BO bisects ∠ABC.
View SolutionIn a given figure, O is centre of circle then ∠x+∠y = ?
 View Solution
View SolutionIn the adjoining figure, O is the centre of a circle in which AB and CD are two diameters. Prove that AC| |BD and AD| |BC. If ∠OBD=50∘, then find the value of ∠AOC.
 View Solution
View SolutionIn the given figure. AB∣CDandO is the midpoint of AD.
View SolutionIn the given figure, O is the centre of a circle such that OA = 5 cm, AB = 8 cm and OD⊥AB meeting AB at C. Find the length of CD.
View Solution