In the given figure, AOB is a diameter of a circle with centre O. Write down the numberical value of ∠ACD+∠DEB.
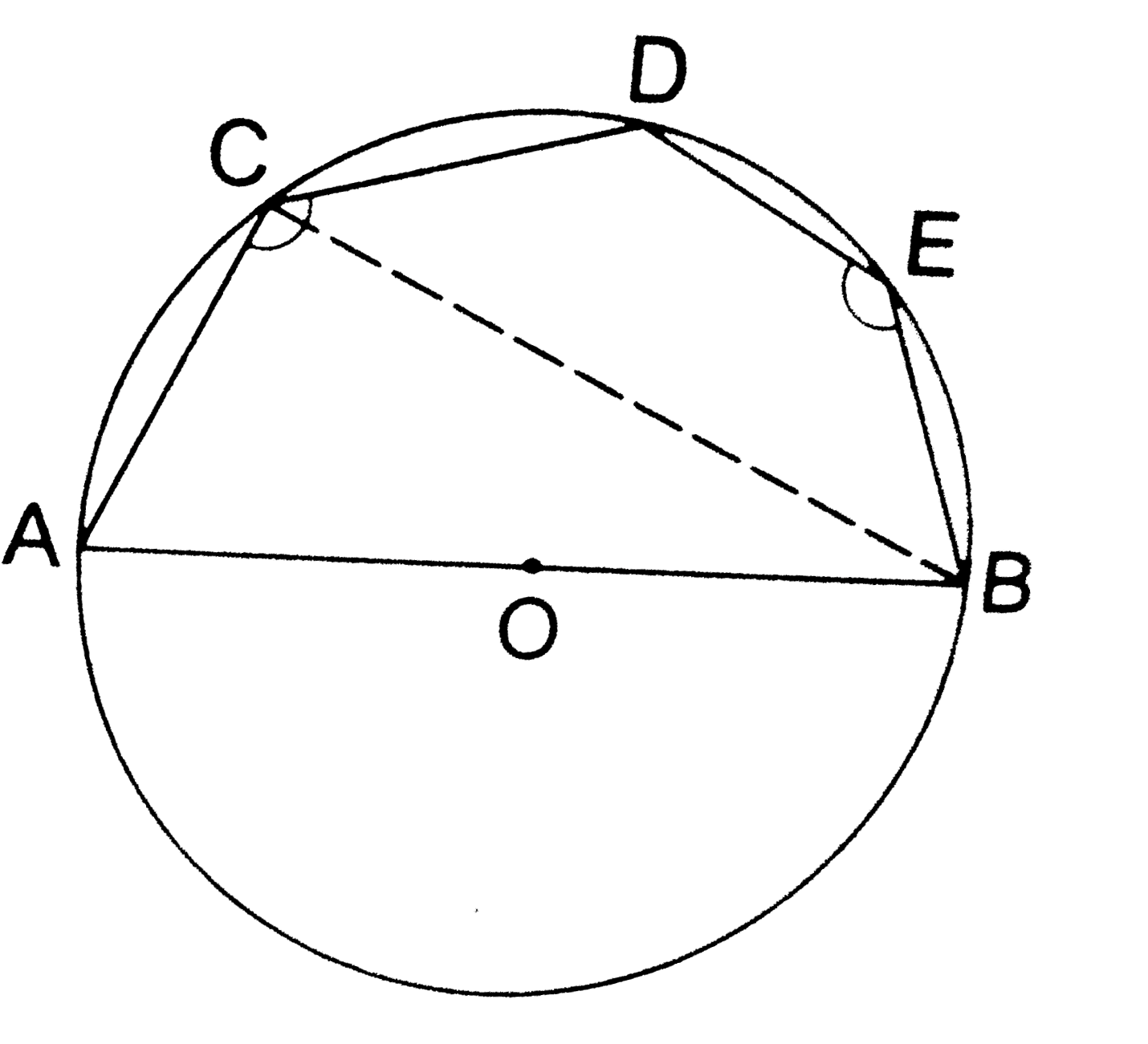
Join BC.
Then, ∠ACD=90∘ [angle in a semicircle ].
Now, DCBE is a circle quadrilateral
∠BCD+∠DEB=180∘
⇒∠ACB+∠BCD+∠DEB=90∘+180∘ [∵∠ACB=90∘]
⇒∠ACD+∠DEB=270∘ [∵∠ACB+∠BCD=∠ACD].
∴ the numerical value of (∠ACD+∠DEB) is 270∘
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A22videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B18videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B16videos
BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGON
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)20videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, AE is the diameter of the circle. Write down the numerical value of ∠ABC+∠CDE.
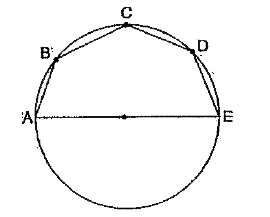 A360∘B540∘C180∘D270∘
A360∘B540∘C180∘D270∘ - Question 2 - Select One
In the given figure, O is the centre of the circle. The value of x is
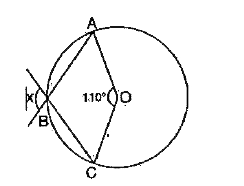 A75∘B55∘C125∘D110∘
A75∘B55∘C125∘D110∘
In the given figure, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ=58∘, find ∠ATQ.
View SolutionIn a given figure, O is centre of circle then ∠x+∠y = ?
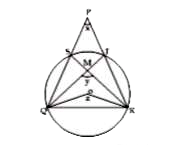 View Solution
View SolutionIn the given figure, AB is diameter of a circle with centre O and AT is a tangent at ∠AOQ=58∘, find ∠ATQ.
View SolutionIn the given figure, AB is a diameter of the circle with centre O and XY is the tangent at a point C. If ∠ACX=35∘, then what is the value (in degrees) of ∠CAB ?
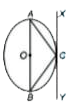 View Solution
View SolutionIn the given figure, AB is a diameter of the circle with centre O and XY is the tangent at a point C. If ∠ACX=35∘, then what is the value (in degrees) of ∠CAB?
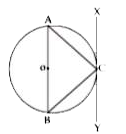 View Solution
View SolutionIn the figure given below, AD is a diameter of a circle with centre O.If AB ll CD, prove that AB=CD
View Solution