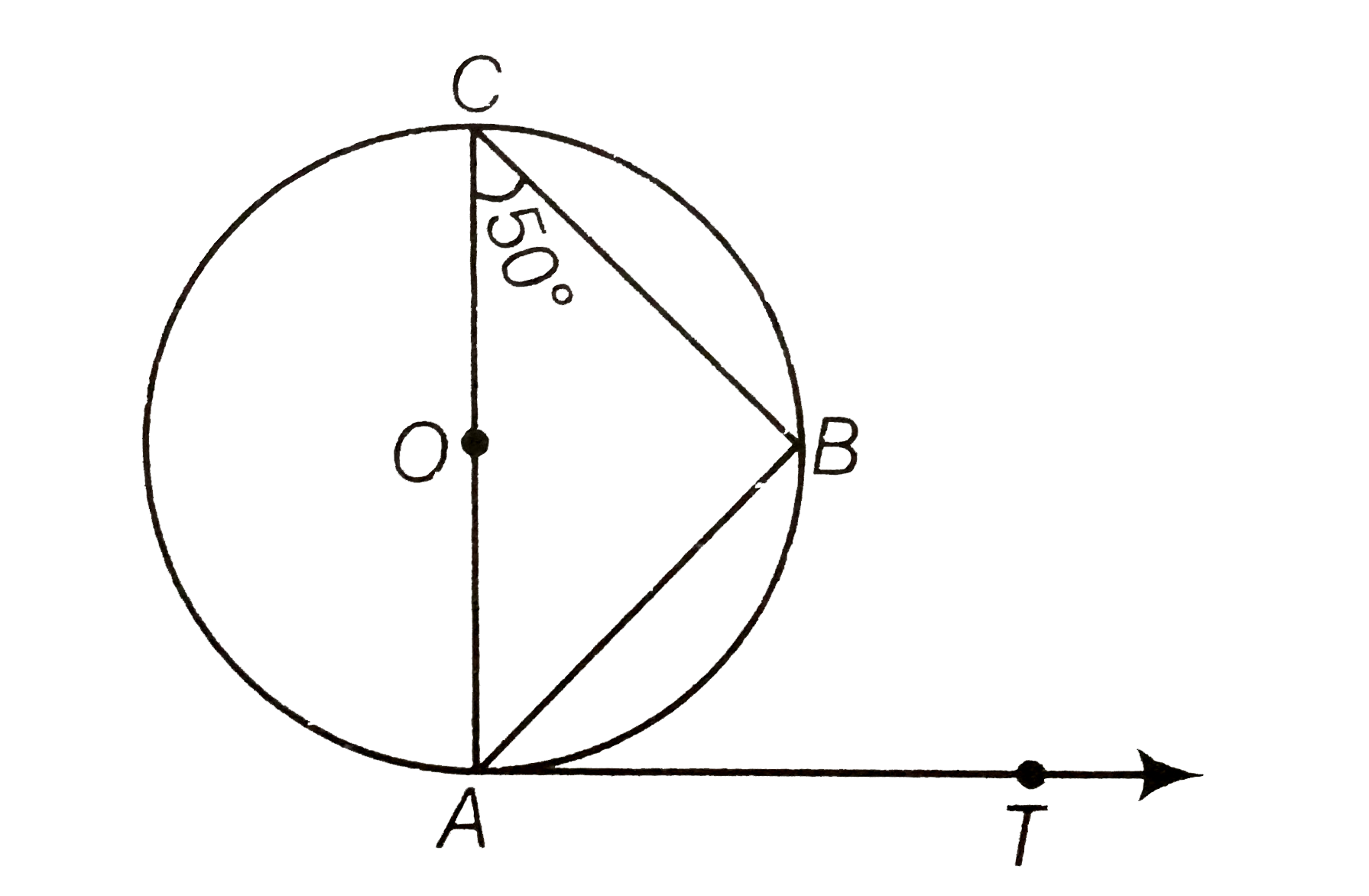
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
45∘
60∘
50∘
55∘
The correct Answer is:C
In figure, AOC is a diameter of the circle. We know that, diameter subtends 90∘ at the circle.
So, ∠ABC=90∘
In ΔACB,∠A+∠B+∠C=180∘
[since, sum of all angles of a triangle is 180∘
⇒∠A+90∘+50∘=180∘
⇒∠A+140=180
⇒∠=180∘−140∘=40∘
∠Aor∠OAB=40∘
Now, AT is the tengent to the circle at point A. So, OA is perpendicular to AT.
∴∠OAT=90∘ [from figure]
⇒∠OAB+∠BAT=90∘
On putting ∠OAB=40∘, we get
⇒∠OAB+∠BAT=90∘
Hence, the value of ∠BAT is 50∘
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.2 VERY SHORT ANSWER TYPE QUESTIONS
10 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.3 SHORT ANSWER TYPE QUESTIONS
10 Videos
- ARITHMETIC PROGRESSIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions
10 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions
7 Videos
Similar Questions
In figure, AB is a chord of the circle and AOC is the diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then angleBAT is equal to : (a) 45∘ , (b) 60∘ , (c) 50∘ , (d) 55∘
View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
View Solution
Knowledge Check
In the figure shown , AB is a diameter of the circle and O is the center of the circle If A=(3,4), then what is the circumference of the circle?
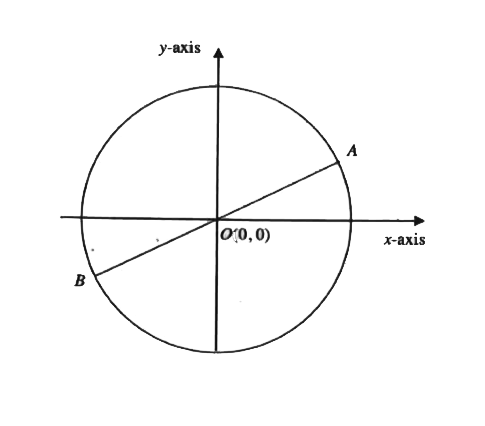 A3B4C4πD10π
A3B4C4πD10π
AB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
View SolutionAB is the diameter and AC is a chord of a circle with centre O such that angle BAC=30∘. The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
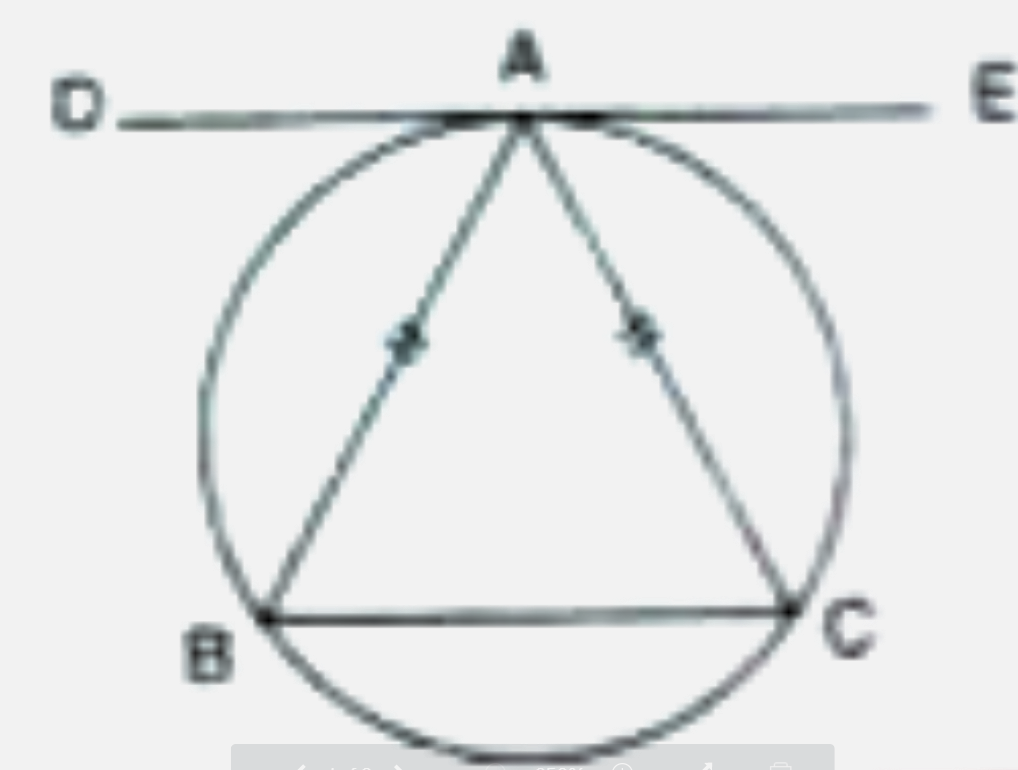
View SolutionThe given figure shows an isosceles triangle ABC inscribed in a circle such that AB=AC. If DAE is a tangent to the circle at point A, prove that DE is parallel to BC.
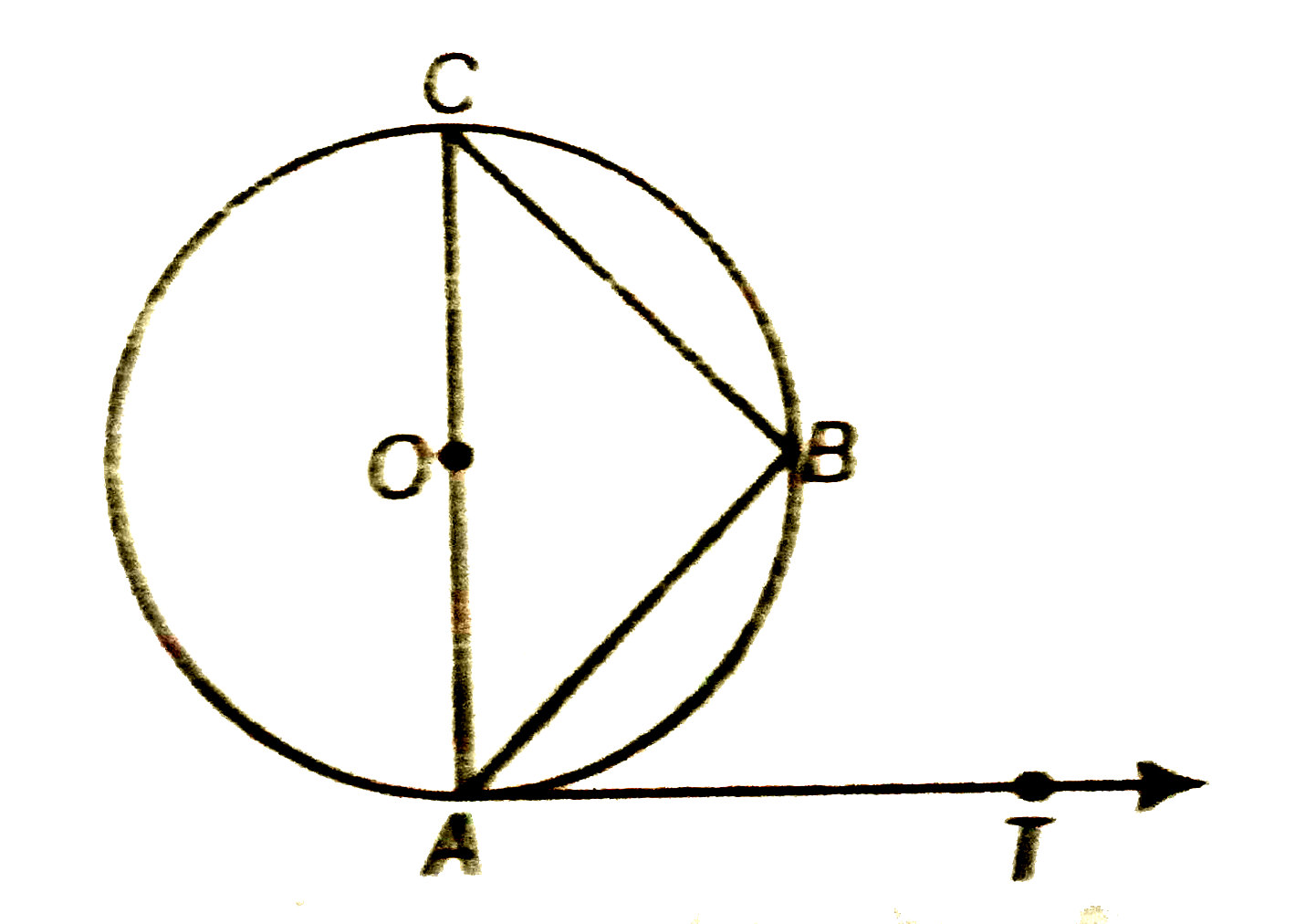
View SolutionIf AB is chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT=∠ACB.
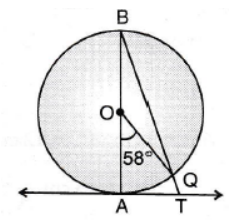
View SolutionIn the given figure, AB is diameter of a circle with centre O and AT is a tangent at ∠AOQ=58∘, find ∠ATQ.
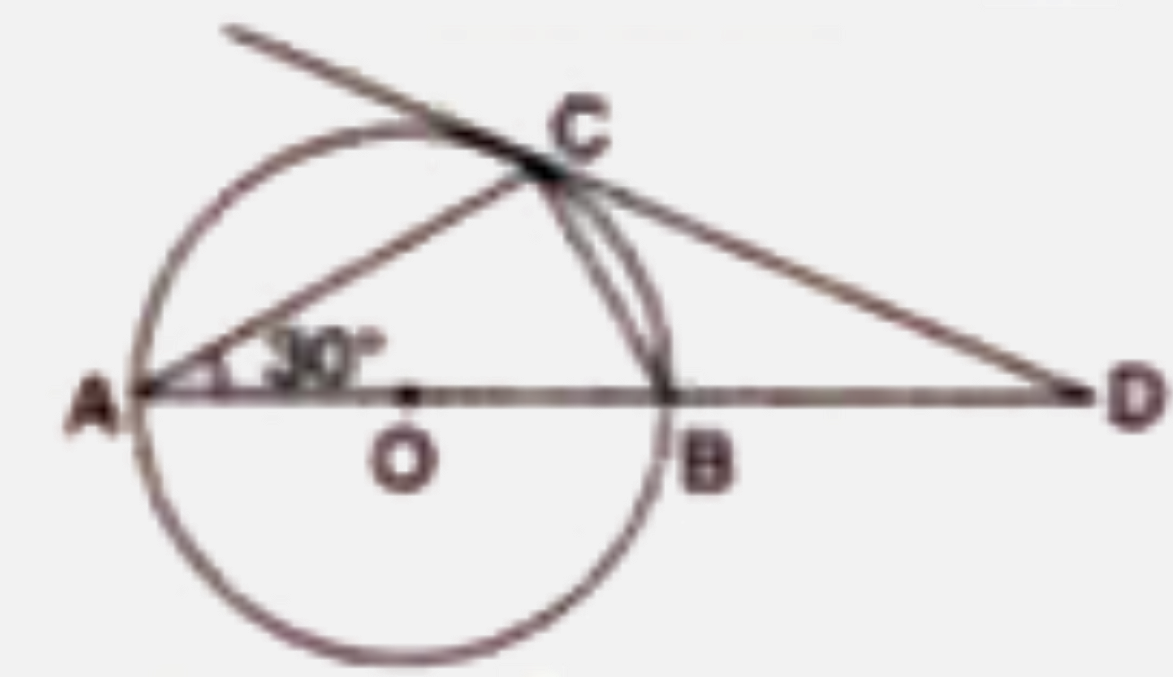
View SolutionIn the given figure AB is the diameter and AC is the chord of a circle such that ∠BAC=30∘. The tangent at C intersects AB produced at D. Prove that :BC=BD.
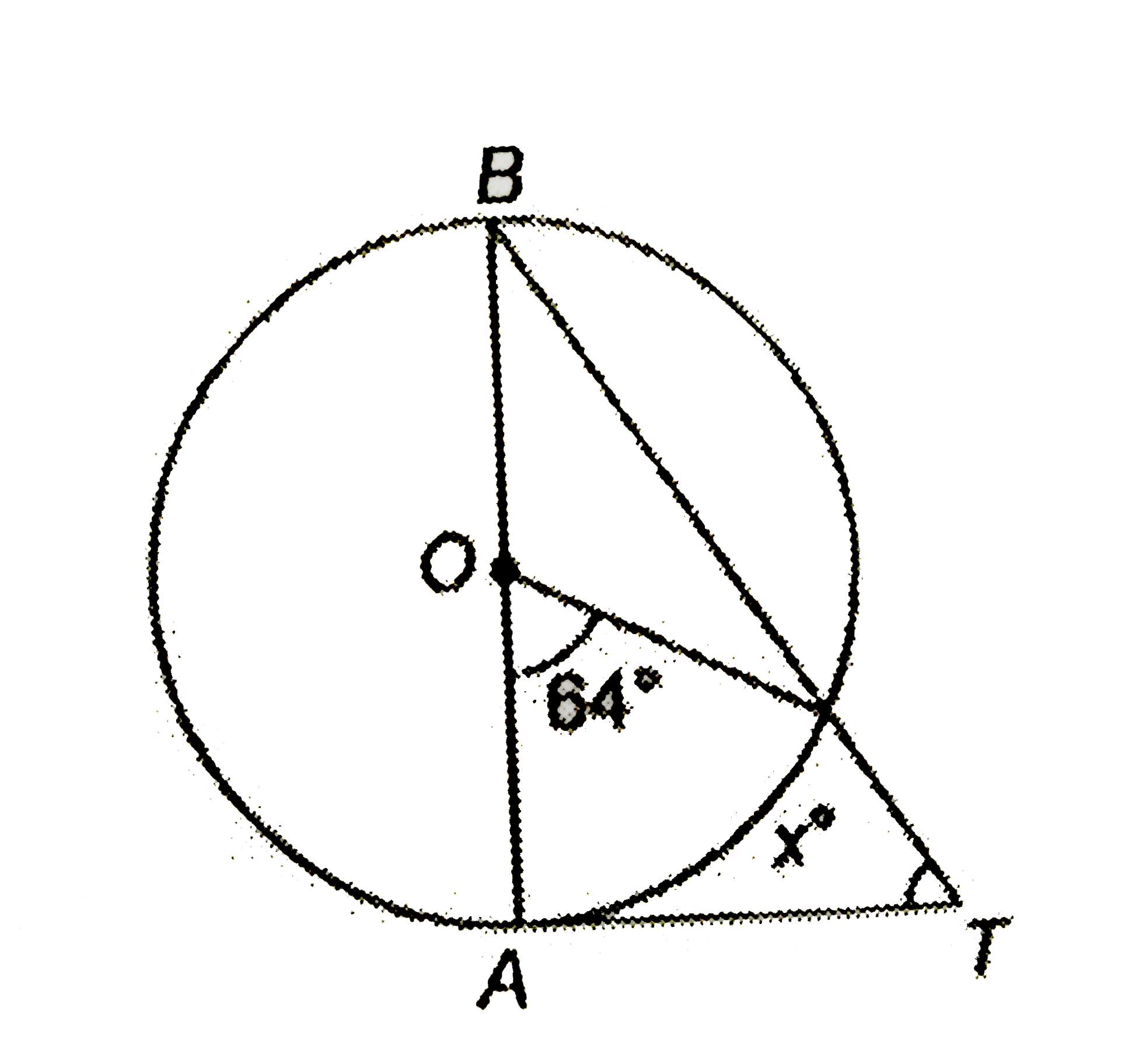
View SolutionIn the giben figure, AB is the diameter of the circle, with centre O and AT is the tangent. Calculate the calue of x.
View Solution
