A straight line AB is divided at C so that AC=3CB. Circles are described on ACandCB as diameters and a common tangent meets AB produced at D. Show that BD is equal to the radius of the smaller circle.
To solve the problem, we need to follow these steps:
Step 1: Understand the Problem
We have a line segment AB divided at point C such that AC=3CB. We need to describe circles on segments AC and CB as diameters and find the relationship between the tangent line and the segments.
Step 2: Define the Lengths
Let:
- CB=r (the radius of the smaller circle)
- Then, AC=3CB=3r
Step 3: Identify the Points
- Let D be the point where the common tangent meets the extended line AB.
- The radius of the smaller circle (on CB) is r.
- The radius of the larger circle (on AC) is AC2=3r2.
Step 4: Use Right Triangle Properties
Since the radius is perpendicular to the tangent at the point of tangency, we can use trigonometry.
For the smaller circle:
- Let BD=x.
- The triangle formed by PQD (where PQ is the radius of the smaller circle) gives us:
sinα=PQPD=rr+x
For the larger circle:
- The radius MN is 3r.
- The triangle formed by MND gives us:
sinα=MNMD=3rMD
Where MD=NC+CB+BD=3r+2r+x=5r+x.
Step 5: Set Up the Equations
From the two expressions for sinα:
1. rr+x
2. 3r5r+x
We can set these equal to each other:
rr+x=3r5r+x
Step 6: Cross Multiply and Simplify
Cross multiplying gives:
r(5r+x)=3r(r+x)
Expanding both sides:
5r2+rx=3r2+3rx
Rearranging gives:
5r2−3r2=3rx−rx
2r2=2rx
Dividing both sides by 2:
r2=rx
Dividing both sides by r (assuming r≠0):
r=x
Conclusion
Thus, we have shown that:
BD=r
This means BD is equal to the radius of the smaller circle.
We have a line segment AB divided at point C such that AC=3CB. We need to describe circles on segments AC and CB as diameters and find the relationship between the tangent line and the segments.
Let:
- CB=r (the radius of the smaller circle)
- Then, AC=3CB=3r
- Let D be the point where the common tangent meets the extended line AB.
- The radius of the smaller circle (on CB) is r.
- The radius of the larger circle (on AC) is AC2=3r2.
Since the radius is perpendicular to the tangent at the point of tangency, we can use trigonometry.
- Let BD=x.
- The triangle formed by PQD (where PQ is the radius of the smaller circle) gives us:
sinα=PQPD=rr+x
- The radius MN is 3r.
- The triangle formed by MND gives us:
sinα=MNMD=3rMD
Where MD=NC+CB+BD=3r+2r+x=5r+x.
From the two expressions for sinα:
1. rr+x
2. 3r5r+x
rr+x=3r5r+x
Cross multiplying gives:
r(5r+x)=3r(r+x)
Expanding both sides:
5r2+rx=3r2+3rx
Rearranging gives:
5r2−3r2=3rx−rx
2r2=2rx
Dividing both sides by 2:
r2=rx
Dividing both sides by r (assuming r≠0):
r=x
Thus, we have shown that:
BD=r
This means BD is equal to the radius of the smaller circle.
Similar Questions
AB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
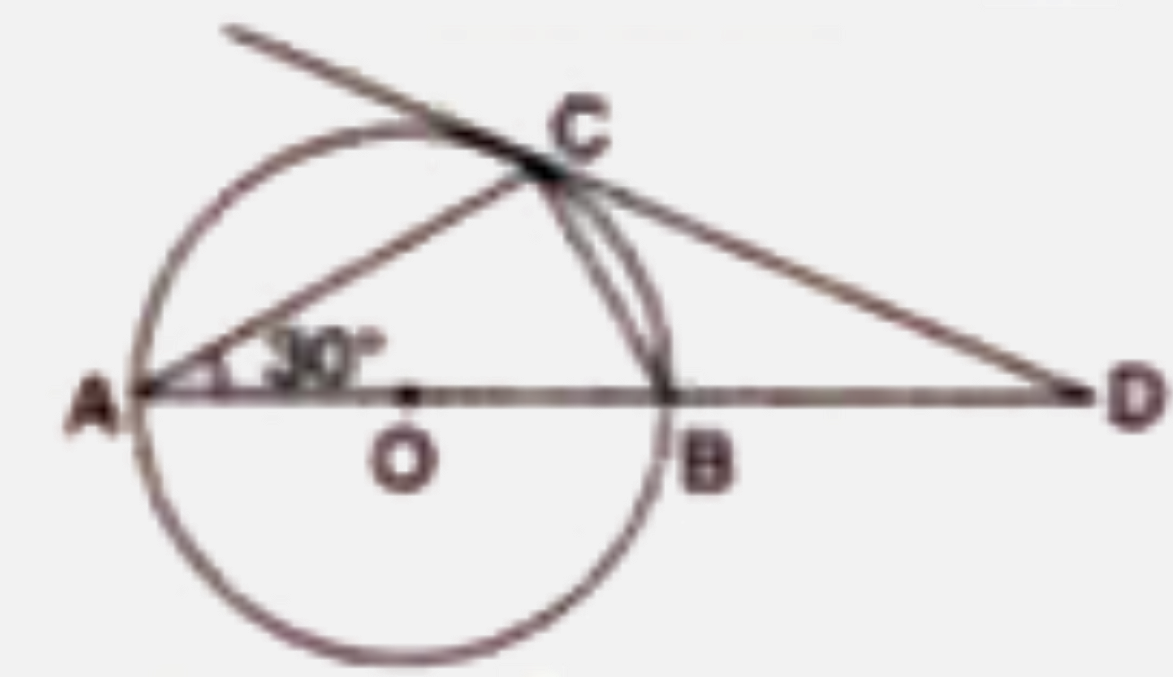
View SolutionIn the given figure AB is the diameter and AC is the chord of a circle such that ∠BAC=30∘. The tangent at C intersects AB produced at D. Prove that :BC=BD.
View SolutionIn figure, AB and CD are common tangents to two circles of equal radii. Prove that AB=CD.

View SolutionAB is the diameter and AC is a chord of a circle with centre O such that angle BAC=30∘. The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
View SolutionAB is a line segment and M is its mid point. Three semi circles are drawn with AM, MB and AB as diameters on the same side of the line AB. A circle with radius r unit is drawn so that it touches all thethree semi- circles. Show that AB=6×r
View SolutionABC is an isosceles trianlge with AB=AC. A circle through B touches side AC at its middle point D and intersects side AB in point P. Show that AB=4×AP.
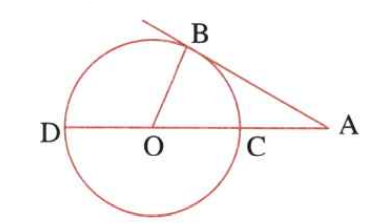
View SolutionIn the given figure, O is the centre of the circle ans AB is a tangent at B. If AB=15 cm and AC=7.5cm, calculate the radius of the circle.
View SolutionIn the given figure, ∠ABC=90∘ and BC is diameter of the given circle. Show that:
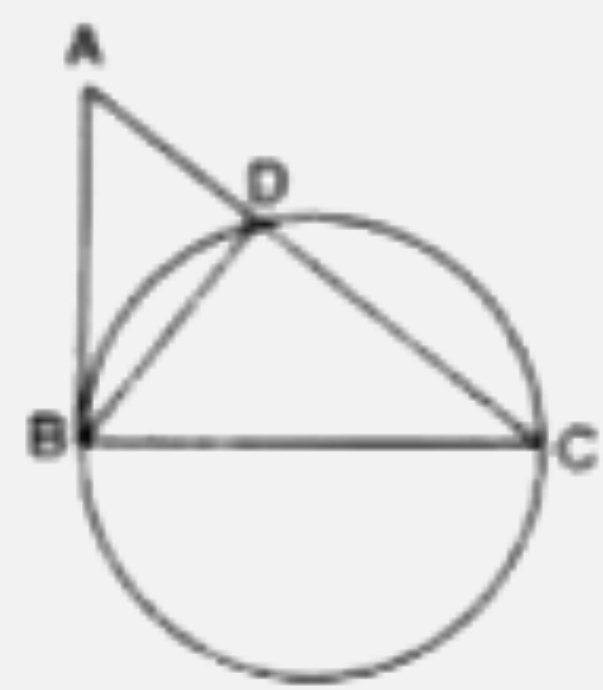
AC×AD=AB2
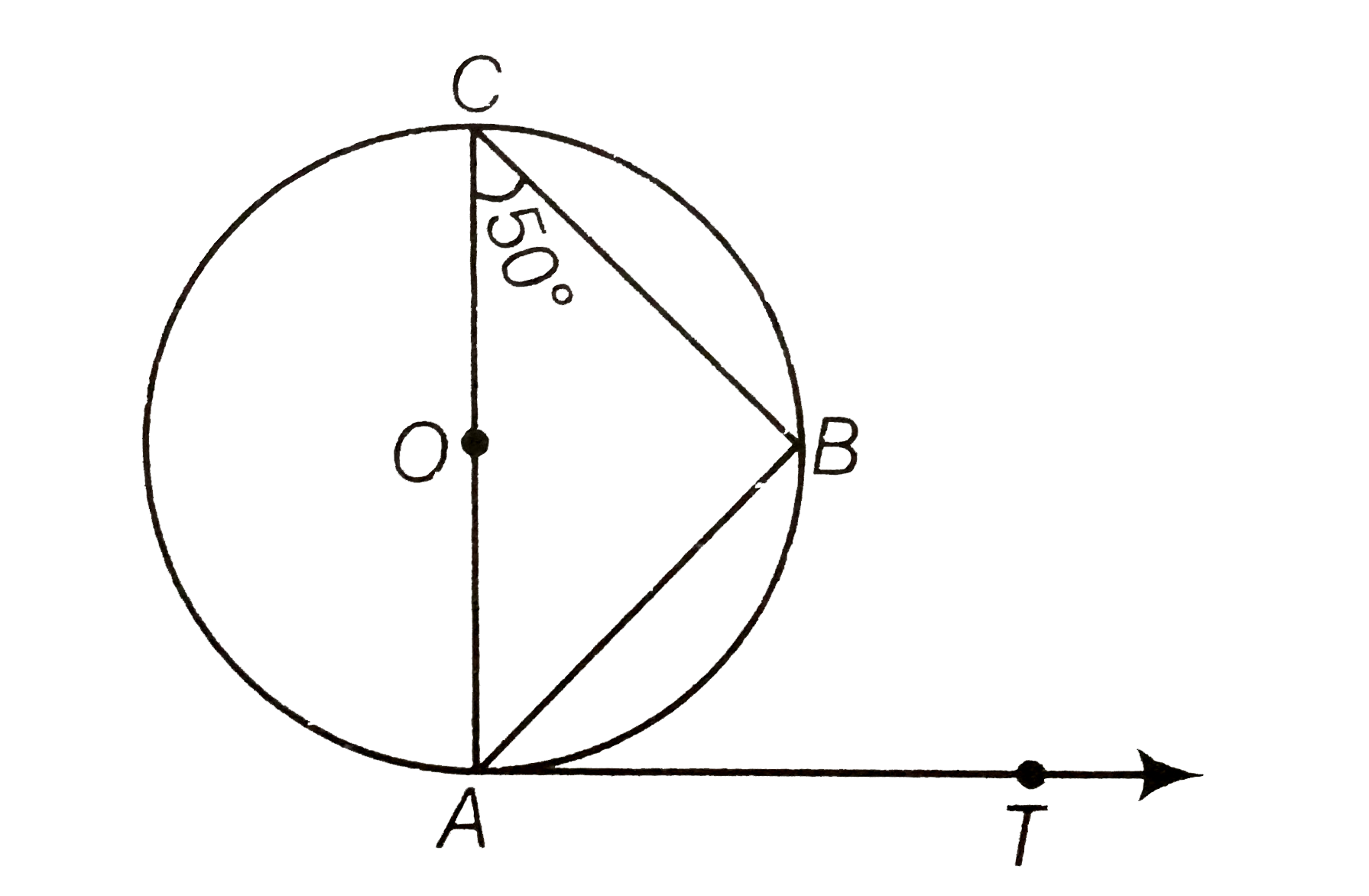
View SolutionIn figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
View SolutionIn the given figure O is the centre of the circle and AB is a tangents at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of the circle.
View Solution
