Find the area bounded by the y-axis, $y = cos x, a n d y = sin x w h e n 0 \leq x \leq \frac{π}{2} .$

A

$2 (\sqrt{2 - 1})$

B

$\sqrt{2} - 1$

C

$\sqrt{2} + 1$

D

$\sqrt{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Given curves $y = sin x$ and $y - cos x$ meet
wher $sin x = cos x$
and $tan x = 1$
$\Rightarrow x = \frac{π}{4}$

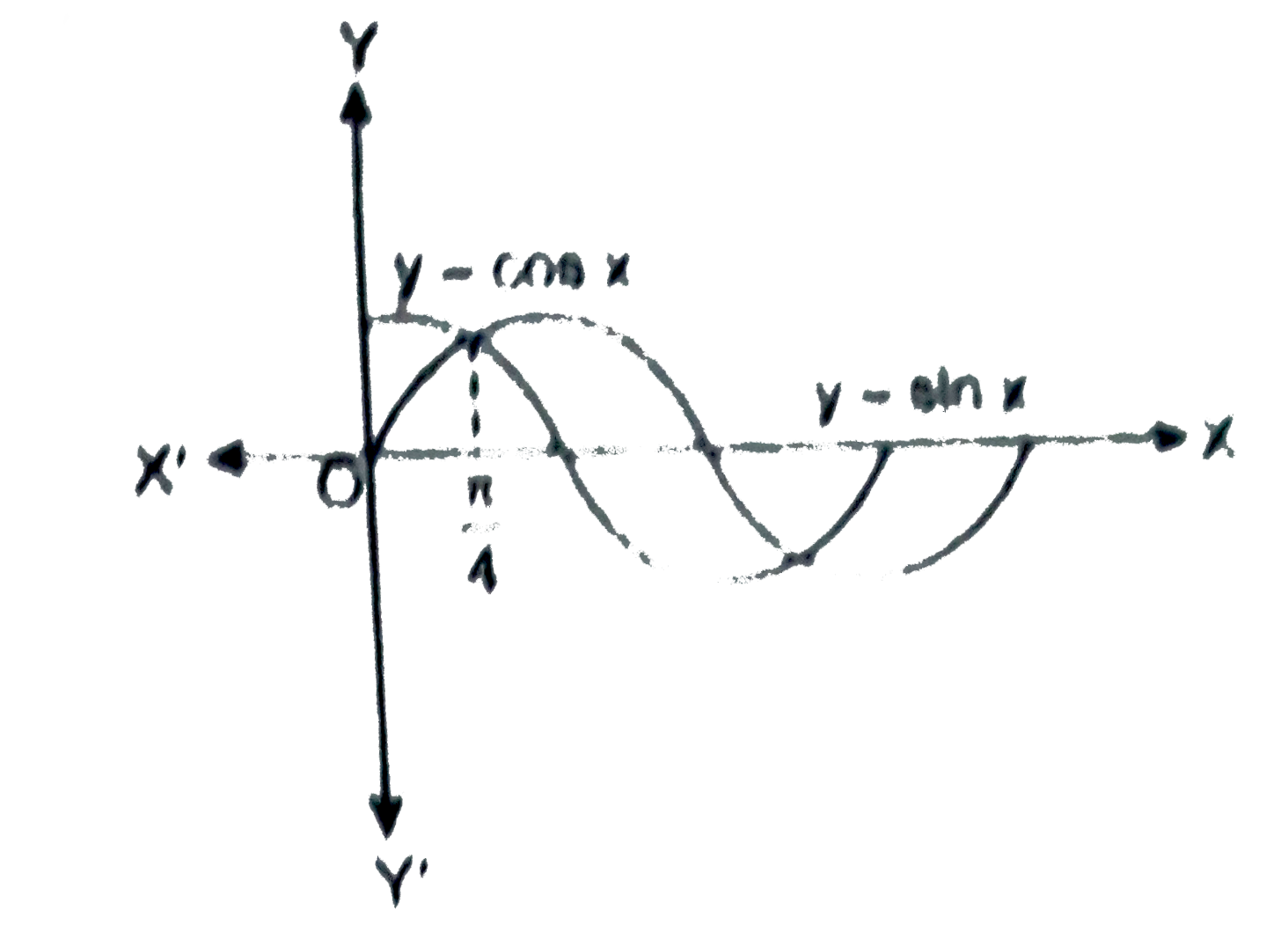
$∴$ Area of required shaded region
$= \int_{0}^{π / 2} (cos x - sin x) d x = {[sin x + cos x]}_{0}^{π / 4}$
$= sin \frac{π}{4} + cos \frac{π}{4} - (0 + 1) = \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} - 1$
$= \frac{2}{\sqrt{2}} - 1 = \sqrt{2} - 1$ sq. units.

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-APPLICATIONS OF INTEGRALS-Miscellaneous Exercise

Home
Ask Doubt
Profile