Question

Draw the graph of the function $f\left(x\right)=2x^2-{\log }_e\left|x\right|$

Explanation

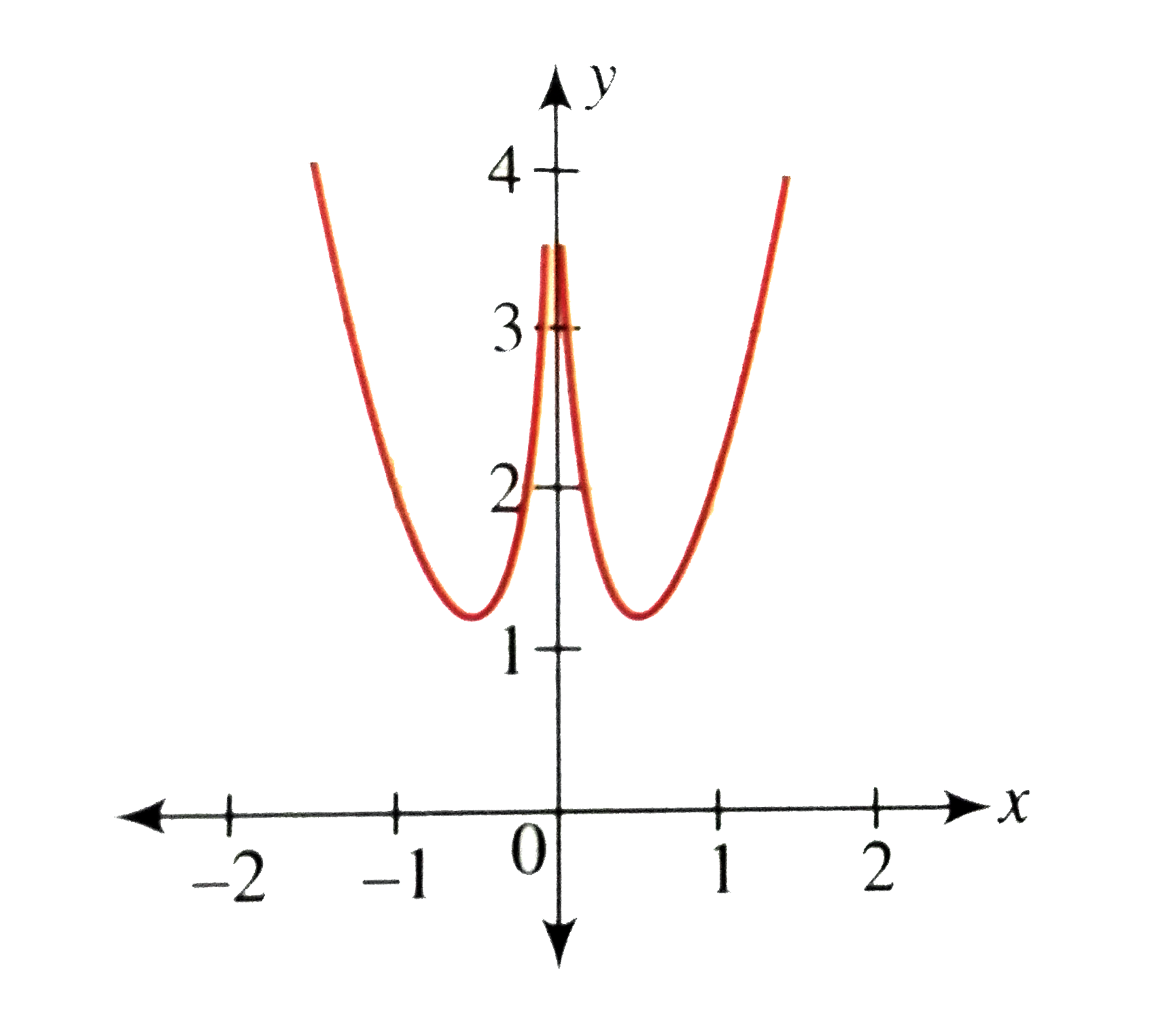
We have `f(x) = 2x^(2)-log_(e)|x|, x ne 0`
Clearly, `f(x)` is an even function, hence its graph is symmetrical about the y-axis.
`underset(xto 0^(+))"lim"(2x^(2)-log_(e)|x|)=infty` and `underset(x to +-infty)"lim"(2x^(2)-log_(e)|x|)=infty` (as difference between the value of `2x^(2)` and ln`|x|` is infinite, `log_(e)|x|` increases very slowly, but `2x^(2)` increases faster)
Also `f^(')(x) = 4x-1/x = (4x^(2)-1)/(x)`
`f^(')(x)=0 rArr x = +-1/2`
From the limiting values of the function at x=0 and at inifinity, we can conclude that `x=+-1/2` are points of minima.
From the above discussion, the graph of the function is as shown in the following figure.