Two points charges are located on the x-axis, q1=−1μC at x=0andq2=+1μc at x=1m.
a. Find the work that must be done by an external force to bring a third point charge q3=+1μC from infinity to x=2m.
b. Find the total potential energy of the system of three charges.
The correct Answer is:A, B, C, D
To solve the problem step by step, we will break it down into two parts as indicated in the question.
Part (a): Work Done by External Force
1. Identify the Charges and Their Positions:
- Charge q1=−1μC at x=0m
- Charge q2=+1μC at x=1m
- Charge q3=+1μC is to be brought from infinity to x=2m
2. Calculate the Final Potential Energy (U_final):
- The potential energy of the system when q3 is at x=2m can be calculated using the formula for potential energy between point charges:
Ufinal=kq1q2r12+kq2q3r23+kq1q3r13
- Where:
- r12=1m (distance between q1 and q2)
- r23=1m (distance between q2 and q3)
- r13=2m (distance between q1 and q3)
- Substituting the values:
Ufinal=k(−1×10−6)(1×10−6)1+k(1×10−6)(1×10−6)1+k(−1×10−6)(1×10−6)2
3. Calculate Each Term:
- k=9×109N⋅m2/C2
- First term:
k−1×10−121=−9×10−3J
- Second term:
k1×10−121=9×10−3J
- Third term:
k−1×10−122=−4.5×10−3J
4. Combine the Terms:
Ufinal=−9×10−3+9×10−3−4.5×10−3=−4.5×10−3J
5. Calculate the Initial Potential Energy (U_initial):
- When q3 is at infinity, there is no interaction with q1 and q2, hence:
Uinitial=kq1q2r12=k(−1×10−6)(1×10−6)1=−9×10−3J
6. Calculate the Work Done (W):
- The work done by the external force is given by:
W=Ufinal−Uinitial
- Substituting the values:
W=(−4.5×10−3)−(−9×10−3)=4.5×10−3J
Part (b): Total Potential Energy of the System
1. Total Potential Energy (U_total):
- The total potential energy of the system is simply the final potential energy calculated above:
Utotal=Ufinal=−4.5×10−3J
Final Answers:
- (a) The work done by the external force is 4.5mJ (or 4.5×10−3J).
- (b) The total potential energy of the system is −4.5mJ (or −4.5×10−3J).
- Charge q1=−1μC at x=0m
- Charge q2=+1μC at x=1m
- Charge q3=+1μC is to be brought from infinity to x=2m
- The potential energy of the system when q3 is at x=2m can be calculated using the formula for potential energy between point charges:
Ufinal=kq1q2r12+kq2q3r23+kq1q3r13
- Where:
- r12=1m (distance between q1 and q2)
- r23=1m (distance between q2 and q3)
- r13=2m (distance between q1 and q3)
- Substituting the values:
Ufinal=k(−1×10−6)(1×10−6)1+k(1×10−6)(1×10−6)1+k(−1×10−6)(1×10−6)2
- k=9×109N⋅m2/C2
- First term:
k−1×10−121=−9×10−3J
- Second term:
k1×10−121=9×10−3J
- Third term:
k−1×10−122=−4.5×10−3J
Ufinal=−9×10−3+9×10−3−4.5×10−3=−4.5×10−3J
- When q3 is at infinity, there is no interaction with q1 and q2, hence:
Uinitial=kq1q2r12=k(−1×10−6)(1×10−6)1=−9×10−3J
- The work done by the external force is given by:
W=Ufinal−Uinitial
- Substituting the values:
W=(−4.5×10−3)−(−9×10−3)=4.5×10−3J
- The total potential energy of the system is simply the final potential energy calculated above:
Utotal=Ufinal=−4.5×10−3J
- (a) The work done by the external force is 4.5mJ (or 4.5×10−3J).
- (b) The total potential energy of the system is −4.5mJ (or −4.5×10−3J).
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 55videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 64videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
Two point charges are located on the x - axis : q1=−e at x=0 and q2=+e at x=a.
The work done by an external force to bring a third point charge q3=+e from infinity to x=2a is.View SolutionFind the work done by some external force in moving a charge q=2μC from infinity to a point where electric potential is 104 V.
View SolutionFind the work done by some external force in moving a charge q=4μC from infinity to a point, where electric potential is 104V
View SolutionTwo point charges are located on the x - axis : q1=−e at x=0 and q2=+e at x=a. A third charge q3=+e is brought to x=2a.
The total potential energy of the system of three charges.View SolutionWhat minimum work must be done by an external force to bring a charge q=3.00μC from a great distance away (take t=∞) to a point 0.500m from a charge =20.0μC ?
View SolutionA charge Q is placed at the origin. The electric potential due to this charge at a given point in space is V. The work done by an external force in bringing another charge q from infinity up to the point is
View SolutionA charge q1=2.00μC is located at the origin , and a charge q2=−6.00μC is located at (0,3.00)m.
(a) Find the total electric potential due to these charges at the point P hose coordinates are ( 4.00,0) m .
( b) Find the change in potential energy of the system of two charges plus a charge q3=3.00μC as the latter charge moves from infinity to point P .View SolutionA point charge q1=4.00nC is placed at the origin, and a second point charge q2=−3.00nC, placed on the x-axis at x = + 20.0 cm. A third point charge q3=2.00nC is placed on the X-axis between q1,andq2. (Take as zero the potential energy of the three charges when they are infinitely far apart).
(a) What is the potential energy of the system of the three charges if q3 is placed at x= + 10.0 cm?
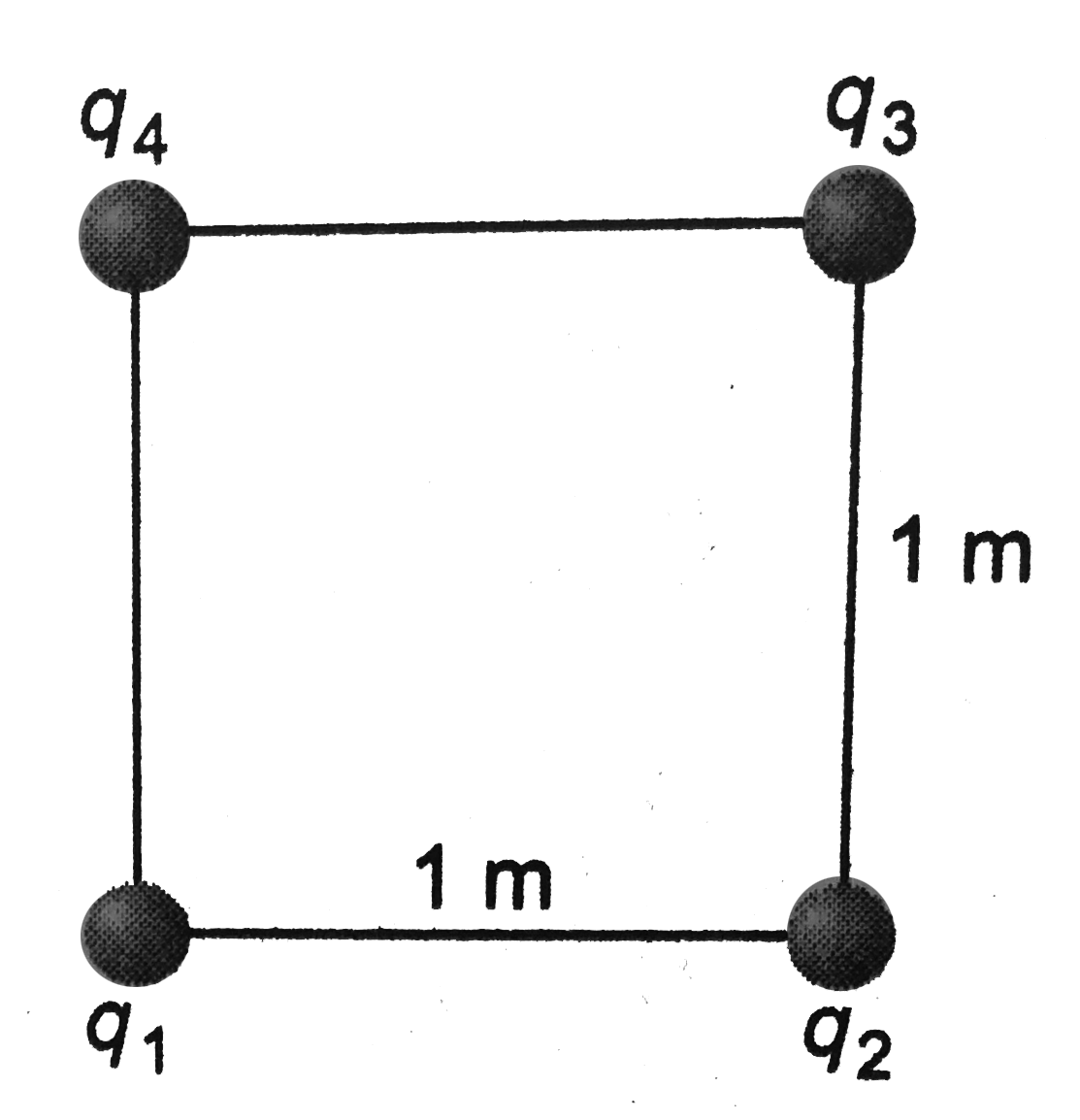
(b) Where should q3 be placed to make the potential energy of the system equal to zero?View SolutionFor charges q1=1μC,q2=2μC,q3=−3μC and q4=4μC are kept on the vertices of a square of side 1m. Find the electric potential energy of this system of charges.
 View Solution
View SolutionFour charges q1=1μC,q2=2μC,q3=−3μCandq4=4μC are kept on the vertices of a square of side 1m. Find the electric potential energy of this system of charges.
View Solution

