Two small spherical shells a and B are given positive charges of 9 C and 4 C respectively and placed such that their centres are separated by 10 m. If P is a point in between them, where the electric field intensity is zero, then the distance of the point P from the centre of A is
5 m
6 m
7m
8 m
The correct Answer is:B
To solve the problem of finding the distance of point P from the center of spherical shell A where the electric field intensity is zero, we can follow these steps:
1. Understanding the Setup:
We have two spherical shells, A and B, with charges QA=9C and QB=4C respectively. The distance between their centers is 10m.
2. Defining Variables:
Let the distance from the center of shell A to point P be r. Consequently, the distance from the center of shell B to point P will be 10−r.
3. Electric Field Due to a Charged Shell:
The electric field E due to a charged shell at a distance r from its center is given by:
E=14πϵ0Qr2
where Q is the charge of the shell and ϵ0 is the permittivity of free space.
4. Setting Up the Equation:
At point P, the electric field due to shell A must equal the electric field due to shell B for the net electric field to be zero:
EA=EB
This translates to:
14πϵ09r2=14πϵ04(10−r)2
We can cancel 14πϵ0 from both sides:
9r2=4(10−r)2
5. Cross Multiplying:
Cross multiplying gives us:
9(10−r)2=4r2
6. Expanding the Equation:
Expanding the left side:
9(100−20r+r2)=4r2
This simplifies to:
900−180r+9r2=4r2
7. Rearranging the Equation:
Rearranging the equation leads to:
9r2−4r2−180r+900=0
Which simplifies to:
5r2−180r+900=0
8. Dividing the Equation:
Dividing the entire equation by 5:
r2−36r+180=0
9. Using the Quadratic Formula:
We can use the quadratic formula r=−b±√b2−4ac2a:
Here, a=1,b=−36,c=180:
r=36±√(−36)2−4⋅1⋅1802⋅1
=36±√1296−7202
=36±√5762
=36±242
10. Calculating the Roots:
This gives us two possible values:
r=602=30(not possible, as it exceeds 10 m)
r=122=6
11. Conclusion:
Thus, the distance of point P from the center of shell A is r=6m.
Final Answer:
The distance of point P from the center of shell A is 6 meters.
We have two spherical shells, A and B, with charges QA=9C and QB=4C respectively. The distance between their centers is 10m.
Let the distance from the center of shell A to point P be r. Consequently, the distance from the center of shell B to point P will be 10−r.
The electric field E due to a charged shell at a distance r from its center is given by:
E=14πϵ0Qr2
where Q is the charge of the shell and ϵ0 is the permittivity of free space.
At point P, the electric field due to shell A must equal the electric field due to shell B for the net electric field to be zero:
EA=EB
This translates to:
14πϵ09r2=14πϵ04(10−r)2
We can cancel 14πϵ0 from both sides:
9r2=4(10−r)2
Cross multiplying gives us:
9(10−r)2=4r2
Expanding the left side:
9(100−20r+r2)=4r2
This simplifies to:
900−180r+9r2=4r2
Rearranging the equation leads to:
9r2−4r2−180r+900=0
Which simplifies to:
5r2−180r+900=0
Dividing the entire equation by 5:
r2−36r+180=0
We can use the quadratic formula r=−b±√b2−4ac2a:
Here, a=1,b=−36,c=180:
r=36±√(−36)2−4⋅1⋅1802⋅1
=36±√1296−7202
=36±√5762
=36±242
This gives us two possible values:
r=602=30(not possible, as it exceeds 10 m)
r=122=6
Thus, the distance of point P from the center of shell A is r=6m.
The distance of point P from the center of shell A is 6 meters.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Match the columns
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
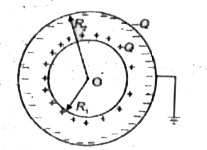
For a spherical capacitor shown at which points the electric field will be zero ? ( r is the distance of point from centre O )
View SolutionTwo point charges of 5μC and 20μC are separated by a distance of 2m. Find the point on the line joining them at which electric field intensity is zero.
View SolutionTwo charges e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is
View SolutionTwo point particle A and B having charges of 4×10−6C and −64×10−6C respectively are held at a separation of 90 cm. Locate the point(s) on the line AB or on its extension where the electric field is zero
View SolutionTwo positive point charges q1=16μC and q2=4μC are separated in vacuum by a distance of 3.0m. Find the point on the line between the charges where the net electric field is zero.-
View SolutionTwo point charges2μC and 8μC areplaced 12 cm apart. Find the position of the point where the electric field intensity will be zero.
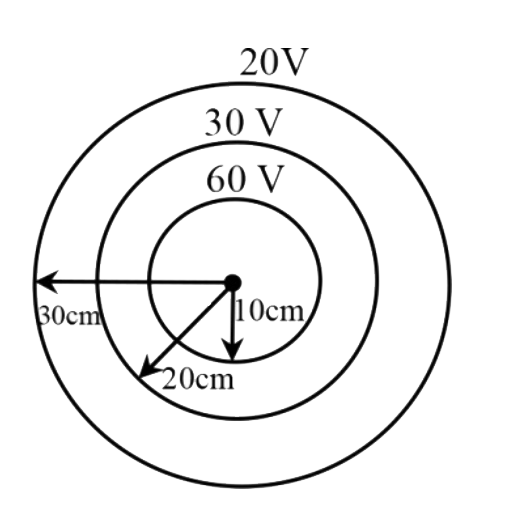
View SolutionA few spherical equipotential surfaces are shown in the figure. The electric field at any point, at a distance x from the centre, is
View SolutionTwo spheres A and B are charged with the charges of +10 and +20 coulomb respectively and separated by a distance of 80 cm. The electric field at point on the line joining the centres of the two spheres will be zero at a distance from the sphere A :
View SolutionTwo electric charges 12μC and −6μC are placed 20cm apart in air. There will be a point P on the line joining these charges and outside the region between them, at which the electric potential is zero. The distance of P from 6μC charge is
View SolutionA conducting shell of radius R carries charge −Q. A point charge +Q is placed at the centre. The electric field E varies with distance r (from the centre of the shell) as
View Solution