The electric field in a region is given by E=αxˆi. Here α is a constant of proper dimensions. Find
a. the total flux passing throug a cube bounded by the surface x=l,x=2l,y=0,y=l,z=0,z=l.
b. the charge contained inside in above cube.
The correct Answer is:A, B, C
a. Electric field is along positive x x-direction. Therfore,field lines are perpendicular to face ABCD and EFGH. At all other four faces field lines are tangential. So, net flux passing through these four facess will be zero. 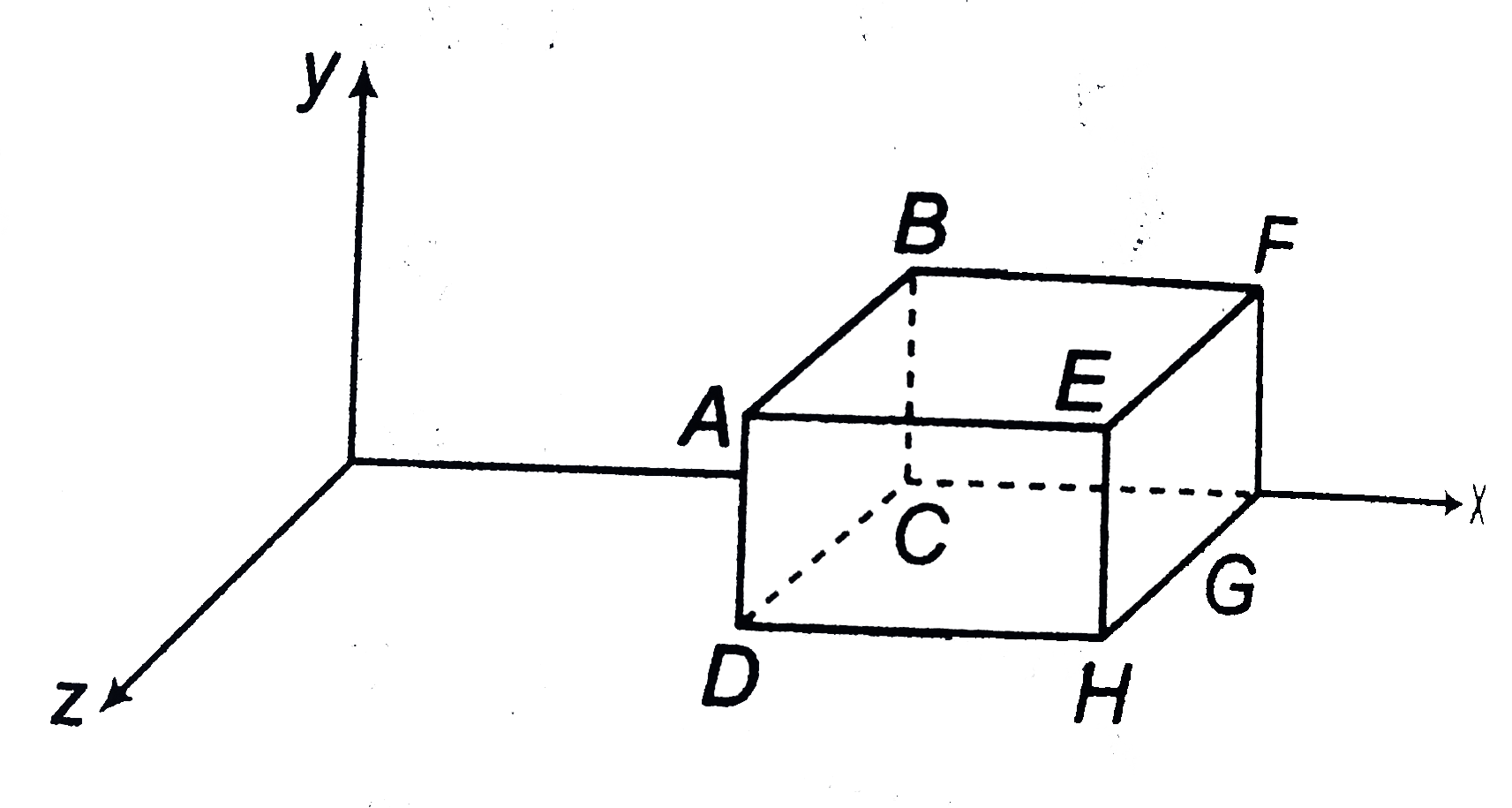
Flux entering at face ABCD at this face x=l 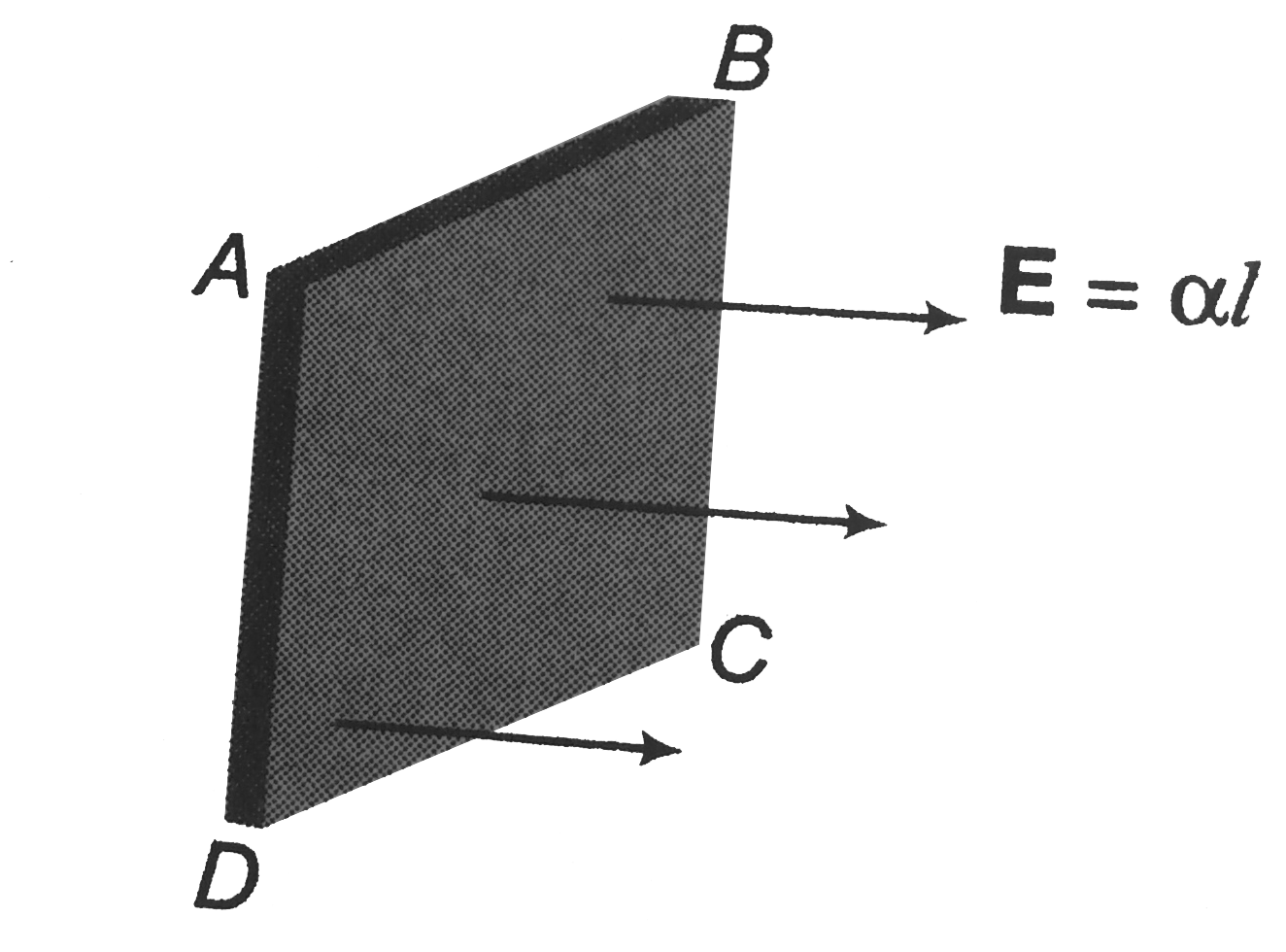
∴E=αlˆi
∴ Flux entering the cube from this face
ϕ1=ES=(αl)(l2)=αl3
Flux leaving the face EFGH At this face x=2l
∴E=2αlˆi
∴ Flux coming out of this face
ϕ2=ES=(2αl)(l2)
=2αl3
∴ Net flux passing through the cube,
ϕnet=ϕ2−ϕ1=2αl3−αl3
=αl3 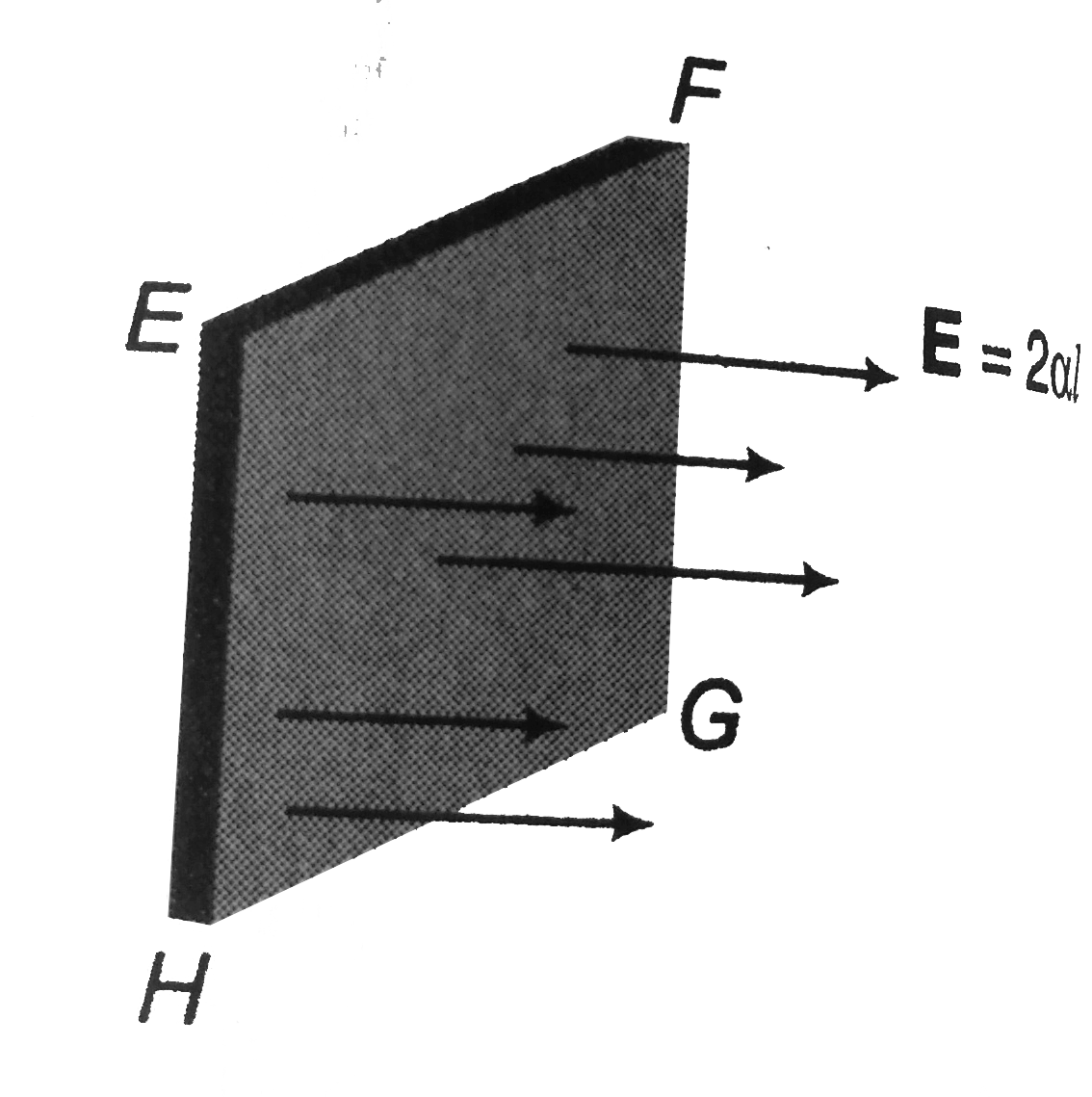
b. From Gauss's law,
ϕnet=qinε0
qin=(ϕnet(ε0)
=αεl3
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.14videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.29videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 83videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
The electric field in a region is given by E=aˆi+bˆj. Hence as and b are constants. Find the net flux passing through a square area of side I parallel to y-z plane.
View SolutionThe electric field in a region is given by E=aˆi+bˆj. Hence as and b are constants. Find the net flux passing through a square area of side I parallel to y-z plane.
View SolutionThe electric field in a region is given by →E=E0axˆi. Find the electric flux passing through a cubical volume bounded by the surfaces x=0,x=a,y=0,y=a,z=0 and z=a.
View SolutionThe electric field in a region is given by E=E0xlˆi. Find the charge contained inside a cubical 1 volume bounded by the surfaces x=0,x=a,y=0,yh=,z=0 and z=a. Take E0=5×103N/C l=2cm and a=1m.
View SolutionThe electric field in a region is given by →E=E0xˆi. The charge contained inside a cubical volume bounded by the surface x=0, x=2m, y=0, y=2m, z=0 and z=2m is nε0E0. Find the va,ue of n.
View SolutionThe electric field in a region is given by →E=E0xι→i. Find the charge contained inside a cubical volume bounded by the curfaced x=0,x=α,y=0,y=α,z=0andz=α. Take E0=5×103NC−1, ι=2cmandα=1cm.
View SolutionThe electric field in a region is given by E=35E0ˆi+45E0j with E0=2.0×103N/C. Find the flux of this field through a rectangular surface of area 0.2m2 parallel to the y-z plane.
View SolutionThe electric field in a region is given by →E=35E0→i+45E0→j with E0=2.0×103NC−1. Find the flux of this field through a recatngular surface of area 0.2m2 parallel to the y-z plane.
View SolutionDue to a charge inside a cube the electric field is Ex=600x1/2,Ey=0,Ez=0. The charge inside the cube is (approximately):
 View Solution
View SolutionThe length of each side of a cubical closed surface is l If charge q is situated on one of the vertices of the cube , then find the electric flux passing through shaded face of the cube.
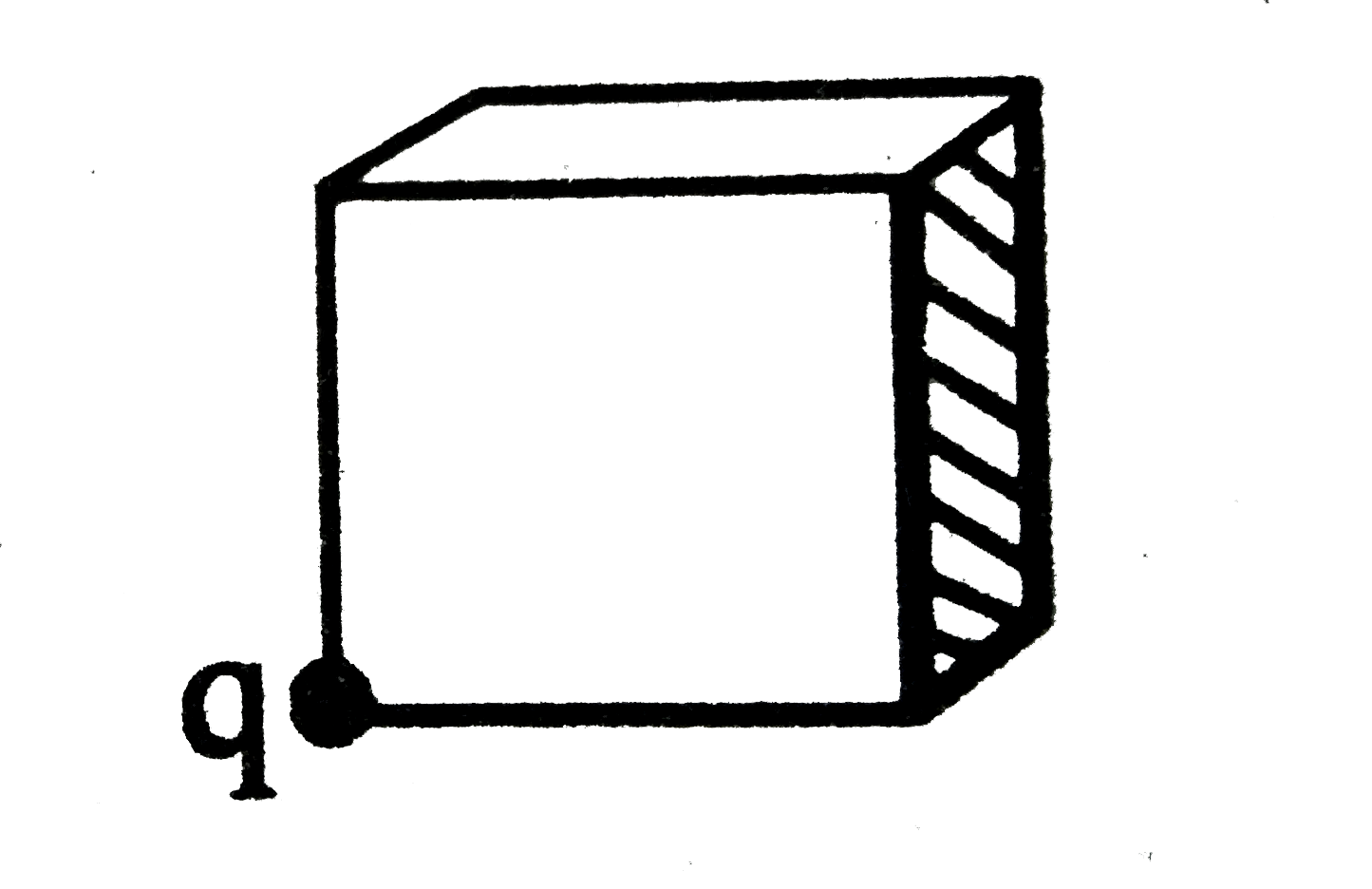 .View Solution
.View Solution

